Алгоритм сжатия текстовых файлов

Аннотация

В статье рассматривается метод эффективного кодирования текстовой информации. В отличие от большинства существующих методов, большая эффективность кодирования и сжатия текста достигается за счет учета вероятностей положения алфавита символов на различных позициях в словах.

Ключевые слова: (генерируются автоматически): кодовая комбинация, эффективное кодирование, символ, знак, позиция, код, слово, сообщение, оптимальный неравномерный код, предложенная методика.

Растущий в настоящее время объем текстовой информации требует разработки новых эффективных и надежных методов ее кодирования, закрытия и передачи. Реализация данного требования возможна за счет уменьшения информационной избыточности передаваемых текстовых сообщений, которое может быть получено за счет их эффективного кодирования.

В общем случае, задача эффективного кодирования сводится к такой обработке передаваемых текстовых сообщений, при которой минимизируется среднее количество двоичных знаков, требующихся для кодирования одного символа сообщения. Это позволяет уменьшить общую длину передаваемого кодового сообщения и, соответственно, времени передачи по каналам связи.

Эффективное кодирование основывается на основной теореме Шеннона для каналов без шума. В теореме доказано, что сообщения, составленные из символов некоторого алфавита, можно закодировать так, что среднее число двоичных знаков на символ будет сколь угодно близко к энтропии источника этих сообщений, но не меньше этой величины.

Из теоремы следует, что при выборе каждого знака кодовой комбинации необходимо стараться, чтобы он нес максимальную информацию. Следовательно, каждый знак должен принимать значения 0 и 1 по возможности с равными вероятностями и каждый выбор должен быть независим от значений предыдущих знаков кодовой последовательности.

При отсутствии статистической взаимосвязи между символами методы построения эффективных кодов были даны впервые К.Шенноном и Н.Фано. Код строится следующим образом: символы алфавита сообщений выписываются в порядке убывания вероятностей. Записанная последовательность разделяется на две подгруппы с равными суммарными вероятностями. Всем символам верхней половины в качестве первого знака приписывается 1, а всем нижним — 0. Каждая из полученных групп, в свою очередь, разбивается на две подгруппы с одинаковыми суммарными вероятностями и т. д. Процесс повторяется до тех пор, пока в каждой подгруппе останется по одному символу. При каждом разбиении к префиксам кодовых комбинаций символов одной подгруппы дописывается кодовый знак 0, к символам другой -1.

Предложенная методика Шеннона — Фано логически не замкнута, т. е. не всегда приводит к однозначному построению кода. Действительно, при разбиении на подгруппы, когда разбить на точно равные по вероятности подгруппы невозможно, имеется неопределенность, какую подгруппу сделать большей по вероятности, а какую меньшей. Таким образом, построенный код может оказаться не самым лучшим. При построении эффективных кодов с основанием а > 2 неопределенность становится еще больше.

От указанного недостатка свободна методика Д. Хаффмена, который дал однозначную, логически замкнутую методику составления эффективных кодов. Она гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом кодовых знаков на символ.

Задача построения оптимального неравномерного кода (ОНК) основания a для некоррелированных алфавитов исходной дискретной последовательности (сообщения) m, состоящий из m символов, формулируется следующим образом:

среди всех возможных кодов основания а без разделительных знаков, которые обладают свойствами префикса, найти код, для которого величина

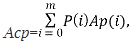(1)

где Аср — средняя длина кодовой комбинации, P(i) - вероятность i-го символа алфавита, Ap(i) — число кодовых знаков кодовой комбинации i-го символа алфавита, минимально возможна.

Для того, что бы предложенный ОНК удовлетворял соотношению (1) необходимо выполнение условий:

1. Если выписать символы в порядке убывания вероятности:
   P(i) >= P(j), (2)
   где i>j, то длительность соответствующих кодовых комбинаций должна удовлетворять соотношению:
   Ap(i) <= Ap(j). (3)
2. Во всяком случае, две последние, но не более чем a, кодовые комбинации, равны по длительности и отличаются значением только последнего кодового знака:
   Ap(m - n⁰) =...= Ap(m - 1) = Ap(m), (4)
   где 2 <= n⁰ <= a
3. Каждая возможная последовательность Ap(m) - 1 кодовых знаков должна либо сама быть кодовой комбинацией, либо иметь своим префиксом используемую кодовую комбинацию [1].

Простейшая статистика текстовых сообщений показывает наличие статистической взаимосвязи не только между символами, но и положением символов на определенных позициях в словах передаваемых сообщений.

Задача построения оптимального неравномерного кода основания a для некоррелированных алфавитов m с учетом положения символа на различных позициях в слове формулируется следующим образом:

среди всех возможных кодов основания а без разделительных знаков, которые обладают свойствами префикса, найти код, для которого величина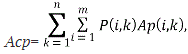
(5)
где Аср — средняя длина кодовой комбинации, P(i,k) - вероятность i-го символа алфавита находящегося на k-й позиции в слове, Ap(i,k) — число кодовых знаков кодовой комбинации i-го символа алфавита на k-ой позиции в слове, n - максимальная длина слова.

Что бы предложенный ОНК, удовлетворял соотношению (5) необходимо выполнение условий:

1. Для каждой позиции символов в слове k є [1…n] если выписать символы в порядке убывания вероятностей:
   P(i,k) >= P(j,k), (6)
   где i > j, то длительность соответствующих кодовых комбинаций должна удовлетворять соотношению:
   Ap(i,k) <= Ap(j,k). (7)

Для двоичного кода методика эффективного кодирования сводится к следующему. Для определенного типа информации (техническая, литературная и т. д.) заранее определяются наиболее характерные частоты появления символов алфавита текстовых сообщений на позициях в словах. По каждой позиции производится ранжирование символов по убыванию частот. В результате этого для каждой позиции получают проранжированную последовательность символов. Символы, стоящие на одинаковых местах в последовательностях (на одной строке таблицы), объединяются в группу символов одного ранга. Последовательно, каждой группе символов одного ранга, ставится в соответствие ОНК, причем, чем больше ранг группы символов (т. е. меньше частота появления), тем больше длительность сопоставляемой при кодировании символу кодовой комбинации.

Оценка эффективности

Проведем оценку эффективности кодирования предложенного и существующих методов. Эффективность использования ОНК принято оценивать с помощью коэффициента сжатия K_сж. Данный коэффициент показывает, во сколько раз уменьшается среднее число двоичных знаков на символ исходного текста при передаче ОНК по сравнению с обычными методами нестатистического кодирования (передачей равномерным двоичным кодом). Для двоичных кодов K_сж определяется отношением: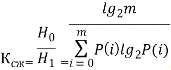
. (8)

Возьмем для алфавита текстовых сообщений на русском языке m = 53 (32 буквы, 10 цифр, 11 служебных знаков). Тогда для равномерного распределения частот символов алфавита печатного текста, построенное по данным [2] получим:

– для соответствующего этому распределению частот первого приближения к энтропии: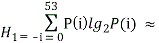
4,85 дв. ед./симв.;

– информационная емкость сообщения:
H₀ = lg₂m = lg₂53 = 6 дв. ед./симв.;

– максимально достижимый выигрыш при кодировании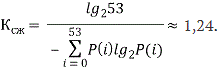

Для предложенной методики эффективного кодирования с учетом распределения вероятностей символов на различных позициях в словах: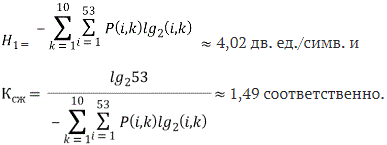

Заключение

Сравнивая полученные результаты, можно сделать вывод, что использование при кодировании предложенной методики приводит к более полному сжатию информации по сравнению с методикой Хаффмена.

Наиболее эффективное использование методики возможно применительно специальной служебной переписке, обладающей меньшим значением энтропии и большей избыточностью.

Литература

1. Новик Д. А. Эффективное кодирование. М.-Л. “Энергия”,1965 г., 236
2. Котов А. П. и др., Основы телеграфии, ВКАС, л.,1958