EFFICIENT TEXT COMPRESSION USING SPECIAL CHARACTER REPLACEMENT AND SPACE REMOVAL

Abstract

Data compression is useful many fields, particularly useful in communications because it enables devices to transmit or store the same amount of data in fewer bits. There are a variety of data compression techniques, but only a few have been standardized. This paper has proposed a new data compression method for general data which based on a logical truth table. Here, two bits data can be represented by one bit in both wire and wireless network. This proposed technique will be efficient for wired and wireless network. The algorithms have evaluated in terms of the amount of compression data, algorithm efficiency, and weakness to error. While algorithm efficiency and susceptibility to error are relatively independent of the characteristics of the source ensemble, the amount of compression achieved depends upon the characteristics of the source to a great extent.

Index terms: Data compression, Truth Table, Compression Ratio, Compression Factor.

1 INTRODUCTION

Date compression is most common and indispensable method in the digital world where transmission bandwidth is limited and wants to quick transmitting data in a network. So we are bound to compress data. Compression is helpful because it helps reducing the data length, such as hard disk space or transmission bandwidth. On the downside, compressed data must be decompressed to be used, and this extra processing may be harmful to some applications [4]. A data compression feature can help reduce the size of the database as well as improve the performance of I/O intensive workloads. However, extra resources are required on the database server to compress and decompress the data, while data is exchanged with the application. The following figure shows a model for a compression system that performs a transparent compression.

Reducing the amount of data required to represent a source of information while preserving the original content as much as possible. The main objectives of data compression are to reduce the amount of data storage space required and reduce the length of data transmission time over the network.

2.1 LOSSLESS COMPRESSION

Two type of compression exists in real world. One is Lossless compression and another is Lossy compression. Lossless and lossy compression are terms that describe whether or not, in the compression of a file, all original data can be recovered when the file is uncompressed.

2.1 LOSSLESS COMPRESSION

With lossless compression, every single bit of data that was originally in the file remains after the file is uncompressed. All of the information is completely restored. This is generally the technique of choice for text or spreadsheet files, where losing words or financial data could pose a problem. The Graphics Interchange File (GIF) is an image format used on the Web that provides lossless compression. Lossless compression algorithms usually exploit statistical redundancy in such a way as to represent the sender's data more concisely without error. Lossless compression is possible because most real-world data has statistical redundancy.

Lossless algorithms mean we can return the original signal. No bits will ignore. It’s numerically identical to the original content on a pixel-by-pixel basis. The Lempel–Ziv (LZ) [1] compression methods are among the most popular algorithms for lossless storage. DEFLATE is a difference on LZ which is utilized for decompression speed and compression ratio, but compression can be slow. DEFLATE is used in PKZIP, gzip and PNG. LZW (Lempel–Ziv– Welch) is used in GIF images. Also noteworthy are the LZR (LZ–Renau) methods, which serve as the basis of the Zip method. LZ methods utilize a table-based compression model where table entries are substituted for repeated strings of data. For most LZ methods, this table is generated dynamically from earlier data in the input. The table itself is often Huffman encoded (e.g. SHRI, LZX). A current LZbased coding scheme that performs well is LZX, used in Microsoft's CAB format.

The very best modern lossless compressors use probabilistic models, such as prediction by partial matching. The Burrows–Wheeler transform can also be viewed as an indirect form of statistical modeling.

In a further refinement of these techniques, statistical predictions can be coupled to an algorithm called arithmetic coding[2]. Arithmetic coding, invented by Jorma Rissanen, and turned into a practical method by Witten, Neal, and Cleary, achieves superior compression to the better-known Huffman algorithm, and lends itself especially well to adaptive data compression tasks where the predictions are strongly context-dependent. Arithmetic coding is used in the bi-level image-compression standard JBIG, and the document-compression standard DjVu. The text entry system, Dasher, is an inverse-arithmetic-coder. Applications of lossless algorithm are medical imaging .Techniques of this algorithm are - Bit Plane Coding, Lossless predictive coding. But In Lossless compression motion compression is not used.

2.2 LOSSY DATA COMPRESSION

Another type of compression, called lossy data compression or perceptual coding, is possible if some loss of reliability is acceptable. Lossy compression reduces a file by permanently eliminating certain information, especially redundant information. When the file is uncompressed, only a part of the original information is still there (although the user may not notice it). Lossy compression is generally used for video and sound, where a certain amount of information loss will not be detected by most users. Generally, a lossy data compression will be guided by research on how people recognize the data in question[3]. For example, the human eye is more sensitive to subtle variations in luminance than it is to difference in color. JPEG image compression works in part by "rounding off" some of this less-important information. Lossy data compression provides a way to obtain the best reliability for a given amount of compression.

A lossy algorithm is which that data cannot return into the original bit. Some bits will ignore. But it will not make any fact. Lossy image compression is used in digital cameras, to increase storage capacities with minimum ruin of picture quality. Similarly, DVDs use the lossy MPEG-2 Video codec for video compression [5].In lossy audio compression; methods of psychoacoustics are used to remove nonaudible (or less audible) components of the signal. Compression of human speech is often performed with even more specialized techniques, so that "speech compression" or "voice coding" is sometimes distinguished as a separate discipline from "audio compression". Different audio and speech compression standards are listed under audio codecs. Voice compression is used in Internet telephony for example, while audio compression is used for CD ripping and is decoded by audio players.The Techniques are -Transform coding (MPEG-X), Vector Quantization (VQ), Sub band Coding (Wavelets),Fractals Model-Based Coding.

3 PROPOSED COMPRESSION METHOD

The proposed technique is shown that, the data bits can be represented by of its half bits. That means 128 bit can be represented by 64 bits, 64 bit can be represented by 32 bits, and 32 bits can be represented by 16 bits.

1GB data can be represented by 512 MB data

This technique is based on the logical truth table, the combination of two bits are given below:

Truth table of proposed technique In table 1: Resultant output is 0 when two input bits are 0 and 0 Resultant output is 1 when two input bits are 1 and 1 Resultant output is when two input bits are 0 and 1 Resultant output is when two input bits are 1 and 0

3.1 PROPOSED DIAGRAM

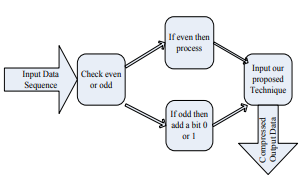
Fig 2: Pseudo generator generates a dynamic key sequence arr

Input data sequence is checked where it is even or odd. If even then process or if odd then add a bit either 0 or 1 depend on last bit. If the last bit of input sequence is 0 then add 0 or if the last bit of input sequence is 1 then add 1.Then it feed to our proposed technique. In this method two bits are collected and converted it into one bit using table 1. So we can get compress data.

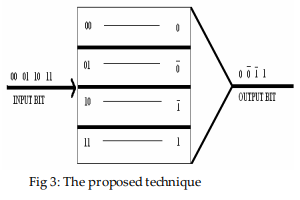
In the above figure we see that the representation of the input bits into output bits at the output terminal where each bit is represented for two bits.

Conventionally we uses two levels for representing digital signal but here we can represent data in four levels which is shown in below.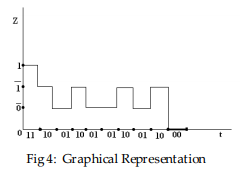

3.2 APPLICATION

Let be considered that
A plane text has been given
x= {1,0,1,1,0,1,0,1,0,0,1,1,0,0,1,1,0,0,1,0} where x=20
Pseudo generator generates a dynamic key sequence
arr=array(0,1,0,1,0,0,1,1,0,1,1,0,1,0,1,0,1,0,1,0)
for each i till to size of x where initial i is equal to 1
and increment i by 1
{
rand=rand(0,19);
y =arr[rand];
}
y= {01010011011010101010} where y=20
X or x and y
So the plane text is encrypted
z= {1,1,1,0,0,1,1,0,0,1,0,1,1,0,0,1,1,0,0,0}
So z can represent by 10 bits

4. COMPRESSION PARAMETERS

These parameters are used for measuring the performance of the proposed method.

4.1 COMPRESSION RATIO

T o calculate the efficiency we have to measure the compression ratio. The compression rate is theoretically 50%. This is strength of this proposed compression technique
%

So the compression rate is 50%
So it will be a great compression method.

4.2 COMPRESSION FACTOR

Compression factor is the inverse term of compression ratio. The value of compression factor is greater than 1 mean compression and value is less than 1 mean imply expansion. Compression can be defined as Compression factor = = = 2
So this data has been compressed.

5 CONCLUSION

Data compression is most consideration thing of the recent world. We have to send a huge amount of data in a limited bandwidth. That is why data has to compress. This proposed compression technique can be useful to send a lot of data in wire and wireless network. The decoder decode to the original data. In a data storage application, although the degree of compression is the primary concern, it is nonetheless necessary that the algorithm be efficient in order for data compression.

6 REFERENCE

1. [1]J. Ziv and A. Lempel, “Compression of individual sequences via variable-rate coding,”Information Theory, IEEE Transactions on, vol.24, no. 5, pp. 530–536, sep. 1978.
2. [2] D. Salomon, Data Compression: The Complete Reference, 2nd ed., 2004. [Online]. Available: http://www.ecs.csun.edu/dxs/DC3advertis/Dcomp3Ad.html
3. [3] A. B. sorting Lossless, M. Burrows, M. Burrows, D. Wheeler, and D.J. Wheeler, “A block-sorting lossless data compression algorithm,” Digital SRC Research Report, Tech.Rep., 1994
4. [4] Introduction to Data Compression by Guy E Blelloch from CMU
5. [5] John Watkinson, The MPEG Handbook,p.4