Введение
Несимметричные короткие замыкания (НКЗ) синхронных машин (СМ) являются опасными режимами, что связано в первую очередь с появлением больших знакопеременных электромагнитных моментов и ударных токов статора [1].
Исследованию несимметричных режимов в синхронных и асинхронных машинах посвящено значительное число работ отечественных и зарубежных ученых. Однако до сих пор остается актуальной задача обеспечения необходимой точности расчета при одновременной простоте получения решения. Методы исследования НКЗ с использованием принципа постоянства потокосцеплений обмоток имеют ограниченную область применения. Известны способы составления и решения для анализа несимметричных режимов дифференциальных уравнений СМ на основе уравнений Парка-Горева [2,3,4]. Строгое решение таких уравнений при НКЗ весьма сложно, так как приходится иметь дело с уравнениями, содержащими периодические коэффициенты. Получить их решение в аналитической форме практически невозможно. Расчеты в этом случае с помощью ЭВМ являются, по существу, расчетами, проводимыми какими-либо вариантами методов численного интегрирования или комбинаций численных и аналитических методов решения дифференциальных уравнений. Такой подход реализован в большинстве промышленных программ и, в частности, в вычислительном комплексе ВКР/ДАКАР, который в настоящее время внедрен в эксплуатацию в энергосистемах Украины и стран СНГ. В зарубежной практике также используется подобный подход (например, приложение Power Systems пакета MATLAB). Однако для общего анализа переходных процессов и выявления экстремальных значений параметров режима дифференциальные уравнения неудобны. Поэтому актуальной задачей является разработка моделей для анализа НКЗ СМ, основанных на аналитическом описании переходных процессов.
В [5] предложена и реализована математическая модель для аналитического описания переходных процессов при симметричных КЗ, а также включениях в сеть синхронных и асинхронных машин, основанная на использовании частотных характеристик с учетом большого числа контуров на роторе.
Цель работы
Разработка методики математического моделирования НКЗ синхронных генераторов путем аналитического описания переходных процессов с использованием информации, получаемой из частотных характеристик проводимостей или сопротивлений со стороны обмотки статора.
Постановка задачи
Важным вопросом при математическом моделировании является способ представления несимметричного режима. Как известно [6], несимметричные КЗ можно представить как включение в месте КЗ некоторой системы напряжений, равных по модулю и направленных противоположно тем, которые были в исходном режиме. Однако для анализа переходных процессов удобнее представлять несимметричные режимы путем включения на симметричные трехфазные системы напряжений прямой (ПП), обратной (ОП) и нулевой (НП) последовательностей, определяемых согласно методу симметричных составляющих.
Рассмотрим случай двухфазного короткого замыкания на выводах синхронного генератора из режима холостого хода. При таком виде несимметрии отсутствует составляющая нулевой последовательности и, следовательно, ток статора будет представляться как сумма токов прямого и обратного следования фаз. Отдельные составляющие переходного тока статора могут быть определены по методике [1] на основе частотных характеристик проводимости СМ со стороны обмотки статора yd ( js ) и yq ( js ) с учетом уточнений, изложенных в [5].
Эту задачу можно решить также на основе правила эквивалентности прямой последовательности [7]. Согласно ему, ток прямой последовательности при несимметричном КЗ равен току трехфазного КЗ в точке, удаленной от действительной точки повреждения на дополнительное сопротивление, величина которого зависит от вида замыкания. Для случая двухфазного КЗ оно равно сопротивлению СМ токам обратной последовательности. Следовательно, ток прямой последовательности при возникновении рассматриваемого несимметричного режима генератора определяется как ток при трехфазном КЗ за внешним сопротивлением, равным сопротивлению обратной последовательности. Структура схем замещения ОП по осям симметрии ротора аналогична структуре схем замещения ПП. Поскольку поле обратного следования фаз вращается в направлении, противоположном направлению вращения ротора, то частотные характеристики входных сопротивлений СМ со стороны обмотки статора x2d ( js ) и x2q ( js ) могут быть получены из соответствующих соотношений для токов ПП путем замены js на j( 2 - s ) .
Высшие гармоники, возникающие при НКЗ в обмотке статора, искажают синусоидальную форму магнитного потока. Это обстоятельство существенно усложняет определение результирующего сопротивления обратной последовательности СМ. Воспользовавшись допущениями, принятыми в [7], результирующее сопротивление ОП можно определить в соответствии со следующим соотношением:
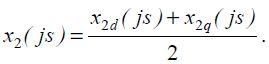
В качестве примера на рис. 1 показана расчетная комплексная схема замещения СМ по продольной оси для режима двухфазного КЗ на выводах генератора.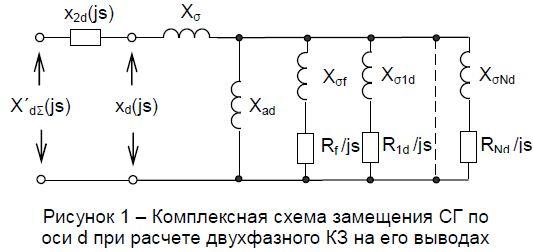
Таким образом, если генератор
по осям d и q характеризуется частотными характеристиками сопротивления xd ( js ) и
xq ( js ) соответственно, то при добавлении в цепь ветви сопротивления рассеяния обмотки статора дополнительного сопротивления x2( js ) частотные
характеристики, соответствующие расчетным эквивалентным схемам замещения, будут определяться следующим образом:
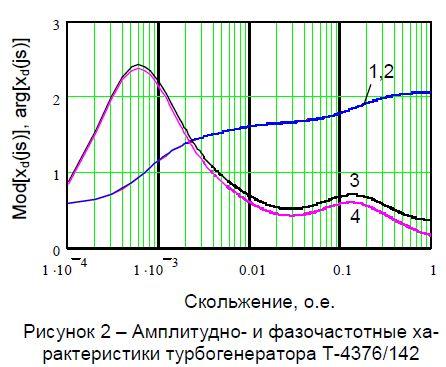
Разрабатываемый в работе алгоритм требует предварительного синтеза на основе схемы, приведенной на рис.1, эквивалентной схемы замещения Г – образного типа. Нелинейное сопротивление x2( js ), зависящее от скольжения, усложняет эту задачу. Поэтому рассмотрим возможность дальнейшего упрощения расчетной схемы замещения. Учитывая, что комплексное сопротивление обратной последовательности при изменении скольжения от 0 до 1 изменяется незначительно, представим его дискретной индуктивностью x2 = Mod[ x2( js )s = 2 ] . На рис. 2 приведены амплитудно и фазочастотные характеристики турбогенератора типа Т – 4376/142, полученные при представлении сопротивления ОП в виде комплексной величины (кривые 1 и 3 соответственно) и дискретного индуктивного сопротивления (кривые 2 и 4). Значения аргументов на рис. 2 увеличены в пять раз. Как следует из анализа рис. 2, амплитуды характеристик практически совпадают во всем диапазоне скольжений. Отличие аргументов в области скольжений от 0 до 0,1 о. е. не превышает 1–2 %. В области больших скольжений указанная погрешность достигает 15–20 %. Это указывает на допустимость принятого упрощения.
Определение переходного тока статора при НКЗ
Аналитическое выражение для определения зависимости изменения изображающего вектора переходного тока прямой последовательности в обмотке статора будет иметь вид:
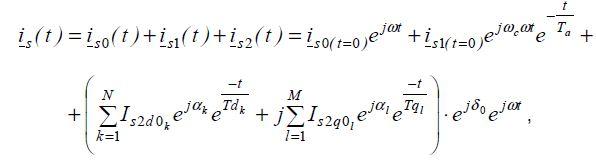
где i ( t ) s0 - установившийся ток ПП, i ( t ) s1 - апериодический ток ПП и i ( t ) s2 - периодический переходный ток ПП.
Определение величин, входящих в (3), предусматривает выполнение расчетных процедур в соответствии с методикой [5]. При этом предварительно рассчитываются комплексные схемы замещения по продольной и поперечной осям ротора структуры, представленной на рис.1, в соответствии с описанной выше методикой. По частотным характеристикам, соответствующим полученным расчетным схемам, определяются параметры эквивалентных схем замещения Г-образного типа.
По изображающему вектору тока прямой последовательности i ( t ) s рассчитываются составляющие токов прямой и обратной последовательностей, а также полные фазные токи:
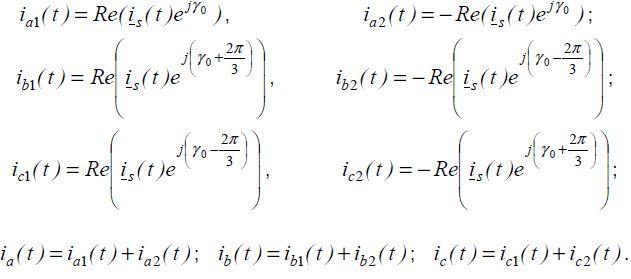
Оценка эффективности предложенной методики
Проверка предложенной методики моделирования производилась для промышленного турбогенератора типа Т-4376/142 ( = 50 ном P МВт; = 3050 ном I А; U 10,5 ном = кВ).
Использовалась экспериментальная частотная характеристика проводимости со стороны обмотки статора yd ( js ), полученная по данным опыта восстановления напряжения после отключения установившегося трехфазного КЗ и соответствующие ей параметры трехконтурной эквивалентной схемы замещения генератора по продольной оси (отн. ед.): Rs0 = 0,00724 ; Xs = 0,1295 ; Xad = 1,282 ; Xaq = 1,077; Rf = 0,0007; Xf = 0,429 ; R1d = 0,006; X1d = 0,765; R2d = 0,0524 ; X2d = 0,190 . Параметры демпферных контуров по поперечной оси принимались такими же, как и в схеме по продольной оси.
Для оценки достоверности исходной информации и методики аналитического расчета электромагнитных переходных процессов на основе частотных характеристик были выполнены расчеты трехфазного КЗ на выводах исследуемого турбогенератора, которые сопоставлялись с экспериментальными данными. На рис. 3 приведены зависимости изменения тока статора (фаза С) при трехфазном КЗ, рассчитанные по методике [5] (кривая 1) и путем численного интегрирования уравнений Парка-Горева (кривая 2). Там же показаны экстремальные значения тока, измеренные в опыте (точки 3).
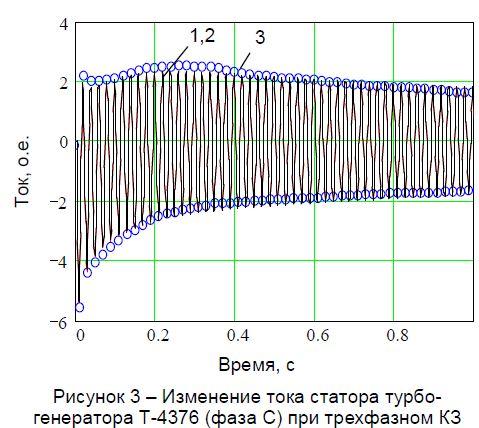
Как следует из анализа рис. 3, имеет место практически полное совпадение расчетных зависимостей во всем диапазоне наблюдения переходного процесса. Отличие ударных токов не превышает 1,5 %. Максимальное несовпадение результатов расчета с экспериментальными данными составляет 11,5 % во временном диапазоне от 0,6 до 0,8 с. При этом погрешность в начале переходного процесса и в установившемся режиме не превышает 9 %.
Таким образом, выполненный анализ указывает на достоверность используемой совокупности электромагнитных параметров исследуемого генератора и эффективность частотного метода применительно к расчету трехфазного КЗ.
Результаты расчета при двухфазном КЗ на выводах генератора приведены на рис.4. Расчеты выполнялись по предлагаемой методике (кривая 1), путем численного интегрирования уравнений Парка-Горева (кривая 2) ис помощью пакетаMATLAB при использовании библиотекиприложения PowerSystem (кривая 3). Поскольку в библиотекеPower System турбогенератор можно представить только двумяконтурами в каждойоси ротора, то при выполнении расчетовдля продольной осибыли определены параметры двухконтурных схем замещения.При этом при решениидифференциальных уравнений Парка-Горева и моделировании в системе MATLAB синтезировались Т – образные, адля предлагаемого в работе способа – Г-образные схемы замещения.
Из анализа рис.4 следует, что результаты расчета токов статора при двухфазном КЗ по предлагаемой методике и по полным уравнениям Парка-Горева практически совпали между собою. Максимальное несовпадение находится в тех же пределах, что и в случае расчета трехфазного КЗ. Отличие от результа тов моделирования в системе MATLAB достигает 15 % во временном диапазоне от 0,15 с до 0,3 с. Это подтверждает эффективность предлагаемой в работе методики математического моделирования НКЗ путем аналитического описания переходных процессов. Близкое совпадение результатов расчета по уравнениям Парка-Горева и на основе предложенного аналитического подхода свидетельствует о том, что полученное выражение для определения тока прямой последовательности практически является решением системы дифференциальных уравнений. Сравнение с экспериментальными данными (рис.4, точки 4) также подтверждает сделанный вывод. Несовпадение результатов расчета ударного тока с опытными значениями не превышает 3,9 %. Максимальная погрешность достигает 8,5 % в диапазоне от 0,5 с до 0,7 с.
Очевидно, что дальнейшее повышение точности моделирования возможно за счет учета многоконтурности ротора турбогенератора. При этом расчет по предлагаемой методике является более эффективным по сравнению с решением дифференциальных уравнений, поскольку время расчета не зависит от числа контуров на роторе. Моделирование в системе MATLAB при числе контуров более двух вообще невозможно. Расчет с использованием описанной в работе методики для трех контуров на роторе по продольной оси позволил повысить точность расчета. Максимальное несовпадение с экспериментальными данными уменьшилось с 8,5 % до 7,9 %.
Вывод
Предложенная в работе математическая модель синхронной машины при нарушении симметрии со стороны обмоток статора, основанная на аналитическом описании переходных процессов, может эффективно использоваться при расчете несимметричных динамических режимов работы.
Список использованной литературы
- Казовский Е. Я., Рубисов Г. В. Переходные процессы в синхронных машинах при анормальных режимах в энергосистеме. – СПб.: Наука, 1994. – 172 с.
- Трещев И. И. Методы исследования электромагнитных процессов в машинах переменного тока. – Л.: Энергия, 1969. – 236с.
- Лупкин В. М. Решение линейных дифференциальных уравнений при двухфазном коротком замыкании синхронной машины // Электричество. – 1979. – №4. – С.8-14.
- Лупкин В. М. Обобщение методов приведения и аналитического решения уравнений несимметричных электрических машин // Электричество. – 1985. – №2. – С.22-29.
- Ламари Абдессалем Бен Атри. Математическое моделирование динамических режимов электрических машин переменного тока на основе статических частотных характеристик: Автореф.дис. канд. техн. наук: 05.09.01 / ДонНТУ. – Донецк, 2004. – 20 с
- Казовский Е. Я. Переходные процессы в электрических машинах переменного тока. – Л.: Энергия, 1962. – 624 с.
- Ульянов С. А. Электромагнитные переходные процессы в электрических системах. – М.: Энергия, 1970. – 520 с.