Математическое моделирование асинхронной нагрузки в режимах группового выбега и самозапуска
Авторы: Сивокобыленко В. Ф., Лебедев В. К., Кукуй К. А.
Источник: Сборник научных статей по электротехнике Донецкого Национального Технического Университета, 2003 г.
В настоящее время для анализа режимов работы энергосистем широко используют методы математического моделирования. Большое развитие получили модели для расчета стационарных режимов, а также, основанные на упрощенных уравнениях Парка–Горева, модели для анализа статической и динамической устойчивости энергосистем.
В последнее время в связи с повышением требований к точности моделирования при разработке и создании высоконадежных систем собственных нужд (С.Н.) ТЭС, АЭС и других ответственных установок с мощными высоковольтными электродвигателями значительно возрос интерес к моделям многомашинных систем электроснабжения, основанным на полных уравнениях Парка–Горева как для двигателей, так и для всех элементов питающей сети. Актуальным является создание универсальных моделей, позволяющих исследовать как кратковременные (короткие замыкания, групповой выбег, АПВ, АВР), так и длительные (пуск, самозапуск) переходные процессы в группе машин (рис. 1) с учетом их взаимного влияния и зависимостей параметров от вытеснения токов и насыщения магнитных цепей.
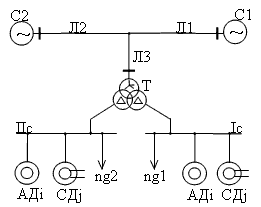
Рисунок 1 – Расчетная схема системы электроснабжения
Весьма распространен в системе С.Н. современных блочных ТЭС и АЭС режим группового выбега электродвигателей 6 кВ после отключения источника питания, имеющий очень большое значение в сочетании с последующим самозапуском для повышения надежности работы энергоблоков. В [1] изложена упрощенная методика расчета перерыва питания и самозапуска электродвигателей С.Н. электростанций, рекомендуемая для работников проектных, наладочных и эксплуатационных организаций. Недостатком данной методики является то, что она основана на упрощенных алгебраических уравнениях элементов С.Н. энергоблока и не позволяет исследовать, например, режимы группового выбега электродвигателей, проходящие, как правило, с взаимным обменом энергией выбегающих агрегатов и требующие использования для описания дифференциальных уравнений. Кроме того, методика [1] также как и другие, например [2], не учитывают совсем или учитывают приближенно явления вытеснения тока в роторах глубокопазных асинхронных двигателей (АД) при самозапуске с помощью усредненных характеристик момента вращения и тока статора электродвигателей. Данная работа направлена на устранение указанных выше недостатков, а также на совершенствование математических моделей многомашинных систем, подробно описанных в [3–4]. При этом ставится задача с помощью дифференциальных уравнений описать также режим группового выбега.
На рис.1 изображена одна из типовых схем системы электроснабжения, содержащая АД, статическую нагрузку и шунты на секциях для моделирования различной степени удаленности коротких замыканий на отходящих от шин присоединениях.
Таким образом, математическая модель рассматриваемой системы электроснабжения будет состоять из дифференциальных уравнений для ее основных элементов: питающего трансформатора с расщепленной обмоткой низшего напряжения, АД, статической нагрузки и активно–индуктивного шунта. Рассмотрим математические модели указанных элементов на основе их полных дифференциальных уравнений. При этом дифференциальные уравнения для АД, в отличие от [4], запишем относительно производных токов статора и контуров ротора, что позволит, как будет показано ниже, получить относительно простые аналитические выражения для определения на каждом шаге расчета неизвестных напряжений на секциях в узлах 1 и 2, необходимых для решения системы дифференциальных уравнений АД.
Выводы
- Разработана математическая модель узла нагрузки, содержащая асинхронные двигатели, статическую нагрузку и шунты для моделирования коротких замыканий различной степени удаленности. Все элементы узла описаны полными дифференциальными уравнениями и выражены относительно производных токов.
- Получены аналитические выражения для определения на каждом шаге расчета напряжения при групповом выбеге асинхронных двигателей.
- Разработанная математическая модель позволяет моделировать групповой выбег, режимы синхронных и несинхронных включений, самозапуска, пуска и другие переходные режимы асинхронной нагрузки и может быть использована как в условиях эксплуатации, так и на стадии проектирования узлов нагрузки, содержащих мощный асинхронный привод.
Литература
- Георгиади В.Х. Методика расчета режимов перерыва питания и самозапуска электродвигателей 3–10 кВ собственных нужд электростанций упрощенными методами. – Москва, ОРГРЭС, 1993 г. – 139 с.
- Ковач К., Рац И. Переходные процессы в машинах переменного тока. – М.Л., Госэнергоиздат, 1963г. – 744 с.
- Сивокобыленко В. Ф., Костенко В. И. Математическое моделирование электродвигателей собственных нужд электрических станций. Донецк, ДПИ, 1979 – 110 с.
- Сивокобыленко В. Ф. Переходные процессы в многомашинных системах электроснабжения электрических станций. Донецк, ДПИ, 1984. – 116 с.