C темпом роста беспроводных технологий все больше интереса представляет система MIMO (Multiple Input Multiple Output – Множественные входы, множественные выходы).
Целью данной работы является исследование методов оценки помехоустойчивости и системы MIMO за счет внедрения методики сингулярного разложения корреляционной матрицы. Для достижения указанной цели, потребовалось решение следующих задач:
- внедрить методику определения помехоустойчивости технологии MIMO за счет сингулярного разложения канальной матрицы;
- произвести необходимые расчеты в вычислительно программном продукте для получения и сравнения результатов.
Таким образом, в данной работе проводится внедрение оценки помехоустойчивости технологии MIMO за счет сингулярного разложения канальной матрицы. Данная методика оценки сравнивается с моделью вычисления помехоустойчивости системы MIMO, для однородных и постоянных во времени каналов.
Для начала рассмотрим методику сингулярного разложения канальной матрицы. Особенностью данного метода является выделение и расчет собственных значений подканала за счет сингулярного разложения матрицы.
Для определения помехоустойчивости системы MIMO данным медом необходимо соблюсти следующий алгоритм:
- Требуется ввести исходные данные, которыми являются количество передающих M и приемных N антенн для системы MIMO, а также величину коэффициента корреляции r.
- Затем приступаем к выбору вида корреляционной матрицы.
- Далее вычисляем обобщенную корреляционную матрицу RMIMO.
- Теперь создаем произвольную матрицу коэффициентов передачи H по формуле:
- Затем необходимо расширить корреляционную канальную матрицу.
- Подверженнее сингулярному разложению канальной матрицы.
- Для дальнейшей работы требуется построение матрицы KQ.
- Вычисление собственных чисел матрицы KQR и H.
- И, наконец, вычисляем помехоустойчивость, используя формулу:
 |
(1) |
где N и M являются количеством приемных, передающих антенн соответственно.
 |
(2) |
 |
(3) |
Пользуясь приведенным выше алгоритмом вычисления помехоустойчивости можно составить блок схему программного вычисления, которая приводится ниже.

Рисунок 1 – Блок схема алгоритма вычисления помехоустойчивости для системы MIMO за счет сингулярного разложении канальной матрицы

Рисунок 2 – Зависимость вероятности ошибки для неоднородных каналов от Eb/N0, дБ системы MIMO различного порядка и коэффициента корреляции r = 0.8 , при двоично фазовой модуляция (BPSK)
Как можно заметить из рисунка 2, представленного выше, показано сравнение помехоустойчивости для системы MIMO c различным количеством приемо–передающих антенн для случая неоднородных каналов при величине корреляции 0.8. Анализируя данные рисунка 2 видно, что при вероятности ошибки 0.001 (10-3) система MIMO3×3 имеет энергетический выигрыш в 4 дБ в отношении системы MIMO2×2. При таком же значении вероятности имеем, что со стороны MIMO4×4 энергетический выигрыш сравнивая с системой MIMO2×2 аж на 7 дБ. Отсюда следует, что с увеличением приемо–передающих антенн будет расти и помехоустойчивость.
Теперь рассмотрим метод вычисления помехоустойчивости системы MIMO для однородных и постоянных во времени каналов. Для вычисления помехоустойчивости данным методом также необходимо соблюсти алгоритм, который приводится ниже.
Алгоритм данной модели состоит из следующих шагов:
- Необходимо ввести исходные данные, которыми является количество приемо–передающих антенн используемой системы MIMO и величина коэффициента корреляции RTX и RRX;
- Затем выбираем вид корреляционной матрицы на приемной и передающей стороне в зависимости от количества антенн используемой системы;
- Далее вычисляем обобщённую корреляционную матрицу для использованной системы MIMO, используя произведение Кронекера:
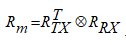 |
(4) |
- На следующем шаге вычисляем собственные числа обобщенной корреляционной матрицы для нашей системы.
- И, на конец, вычисляем помехоустойчивость, используя формулу:
 |
(5) |
Используя приведенный выше алгоритм, была составлена блок схема вычисления помехоустойчивости.
На рисунке 4 представлены графики помехоустойчивости для систем SIMO (Единичный вход, множественный выход) и MIMO которые были рассчитаны в специальном математическом пакете при величине корреляции 0.8. Из данного рисунка можно видеть получение следующих результатов:
- Относительно системы MIMO, при величине вероятности ошибки равной 10-3 система MIMO3×3 имеет энергетический выигрыш на 7 дБ в отношении системы MIMO2×2. Что касается системы MIMO4×4 , то тут энергетический выигрыш уже составляет 9 дБ.
- При том же значении вероятности ошибки выигрыш между MIMO2×2 и SIMO1×2 составляет 3 дБ. Также выигрыш между MIMO3×3 и SIMO1×3 составляет 3 дБ, а выигрыш между MIMO4×4 и SIMO1×4 равен 2.5 дБ.
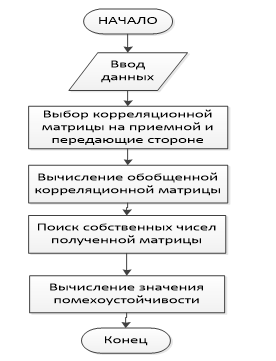
Рисунок 3 – Блок схема алгоритма вычисления помехоустойчивости для системы MIMO в условиях однородного и постоянного во времени канала

Рисунок 4 – Зависимость вероятности ошибки от Eb/N0 для систем SIMO и MIMO при r =0.8, модуляция BPSK
Подводя итоги можно сказать, что предложения методика расчета помехоустойчивости за счет внедрения сингулярного разложения канальной матрицы имеет меньшие результаты энергетического выигрыша по сравнению с методикой определения помехоустойчивости для однородных и постоянных во времени каналов. Сравнивая результат можно сказать, что выигрыш MIMO3×3 относительно MIMO2×2 использующий методику сингулярного разложения корреляционной матрицы уступает на 3 дБ в отношении методики определения помехоустойчивости для однородных и постоянных во времени каналов. Рассматривая систему MIMO4×4, энергетический проигрыш составляет 2 дБ. Отсюда следует, что с увеличением количества приемо–передающих антенн и равномерного распределения нагрузки предложенная методика будет предпочтительнее, поскольку с увеличением антенн выигрыш будет только расти.
Список использованной литературы
1.W. C. Jakes. Microwave Mobile Communications//IEEE Press, New York, 1974. p.39–45.
2.Н. Н. Chen, Y. Y. С. Tsai, and W. Chang, "Uplink Synchronization Control Technique and its Environment–Dependent Performance Analysis," Electronics Letters, vol. 33, pp. 1555 –1757, Nov. 2003.
3.Лысяков Д. Н. Анализ и синтез адаптивной обработки сигналов в системах радиосвязи с параллельной передачей информации по пространственным подканалам: дис. канд. физ. мат. наук. – Нижний Новгород , 2010. – 123с.