Аннотация
В данной статье мы рассмотрим самый актуальный способ увеличения пропускной способности и емкости беспроводных систем связи, а именно технологию MIMO (Multiple Input Multiple Output) с сочетанием преимуществ пространственного разнесения, временного кодирования и простоты обработки сигнала.
Введение
Современное поколение беспроводных систем связи обеспечивает передачу различных видов информации на высоких скоростях, сохраняя при этом высокое качество. Повышение качества работы или уменьшение вероятности ошибки в системе радиосвязи при многолучевом распространении сигнала является наиболее сложной задачей.
Основными характеристиками технологии MIMO (Multiple Input Multiple Output) являются помехоустойчивость и спектральная эффективность, зависящие от таких параметров, как средняя мощность принимаемого сигнала, тепловой шум приемника, направление движения абонента, характер расположения препятствий на пути распространения сигнала, угол прихода лучей на антенны, пространственный разнос между антеннами. В многолучевых каналах разнос антенн – это практичная, эффективная, а, следовательно, широко распространенная техника для уменьшения влияния замираний[2].
Коэффициенты корреляции
Пространственная корреляция для канала с замираниями в общем случае определяется выражением [3]:
 |
(1) |
где H – матрица коэффициентов передачи канала (канальная матрица); vec(H) – обозначает вектор размера Nr × Nt , составленных из столбцов матрицы H; Nr – количество приемных антенн; Nt – количество передающих антенн.
При этом предполагается [3], что наибольшая концентрация препятствий расположена около приемных и передающих антенн, тогда матрица пространственной корреляции RM для системы MIMO определяется формулой:
 |
(2) |
где ⊗ – оператор Кронекера, (•)T – транспонирование матрицы; RX ,RRX – матрицы пространственной корреляции на передающей и приемной стороне соответственно.
При этом канальная матрица с учетом влияния корреляции сигналов может быть рассчитана следующим образом [4]:
 |
(3) |
В случае, когда коэффициент корреляции сигналов в соседних антеннах на передающей стороне равен rTX и на приемной – rRX , для определения матрицы коэффициента корреляции используются следующие выражения [2, 3]:
 |
(4) |
Рассмотрим определение коэффициента пространственной корреляции. В случае типовых условий распространения сигнала радиоволны приходят на приемные антенны с определенной азимутальной расходимостью. В качестве примера рассмотрим ситуацию, когда рассеянная энергия поступает на вход приемника с непрерывного диапазона азимутальных углов (рис. 1), где α обозначает ширину сектора принимаемого рассеянного сигнала (в радианах), а угол θ0 –начальный угол сдвига.

Рис. 1 – Угловое рассеивание мощности p(θ)
При этом среднее угловое рассеивание для такого случая равно [5, 6]:
 |
(5) |
Частные случаи выражения (5) дают лучшее понимание определения углового рассеивания. Прием сигнала с одного направления соответствует α = 0, что приводит к результату Λ = 0 . Если сигнал принимается со всех сторон, то тогда α = 2π , что дает результат Λ = 1.
Пространственный коэффициент корреляции rs(d) определяется выражением:
 |
(6) |
Данное выражение верно для относительно малых d , однако большинство практических применений пространственного разноса используют именно такие расстояния между антеннами. На рис. 2 показана зависимость коэффициента пространственной корреляции rs (d) от относительного расстояния между антеннами d /λ при фиксированной ширине сектора принимаемого рассеянного сигнала α.

Рис. 2 – Зависимость rs от d /λ при фиксированной ширине сектора принимаемого сигнала α
Из рис. 2 следует, что при малых значениях угла рассеивания величина коэффициента пространственной корреляции стремится к единице, а при больших значениях этого угла величина коэффициента пространственной корреляции быстро уменьшается.
Помехоустойчивость приема в каналах с корреляцией
Вероятность ошибки при когерентном приеме с выхода n статистически неоднородных независимых релеевских каналов при любом виде манипуляции, при произвольной структуре двоичных сигналов в каждом канале, определяется формулой [1]:
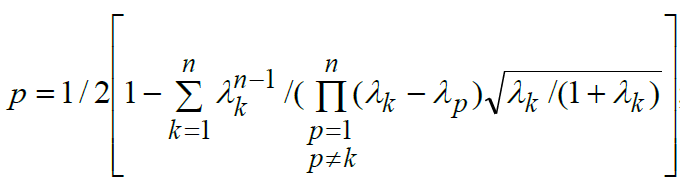 |
(7) |
где λk – собственные числа матрицы отношений энергии сигнала к спектральной плотности мощности шума KMISOQMISO, которая рассчитывается из общей матрицы KQ, но учитывает пространственную и кодовую корреляцию (матрица R ).
Матрица K коэффициентов передачи канала записывается в общем виде [1]:
 |
(8) |
матрица Q отношений сигнал/шум записывается в общем виде:
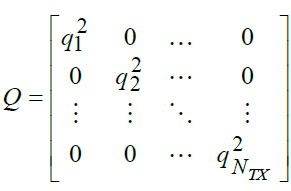 |
(9) |
где λk – коэффициент передачи канала k [1]. k = 1, 2, …, NTX ;NTX – количество передающих антенн в системе MISO.
Список использованной литературы
1. Андронов И. С., Финк Л. М. Передача дискретных сообщений по параллельным каналам. М.: Советское радио, 1971. 408 с.
2. Носов В. И. Методы повышения помехоустойчивости систем радиосвязи с использованиием технологии MIMO и пространственно–временной обработки сигнала: Монография. – Новосибирск: СибГУТИ, 2014. 316 с.
3. A. van Zelst. A Compact Representation of Spatial Correlation in MIMO Radio Channels//Proc. of the 10th Mediterranean Electrotechnical Conf. (MELECON). 2000. Vol. 3. May 2000. P. 1218–1221.
4. D. Shiu, G. J. Foschini, M. J. Gans, J. M. Kahn. Fading Correlation and Its Effect on the Capacity of Multielement Antenna Systems // IEEE Transaction On Communications. Vol. 48. No. 3. 2000. P. 502–513.
5. H. Bizaki. MIMO systems, theory and applications. InTech, 2011. 500 p.
6. G. D. Durgin and T. S. Rappaport. A Basic Relationship Between Multipath Angular Spread and Narrowband Fading in a Wireless Channel. IEEE Electronics Letters. 1998. Vol. 34. No. 25. P. 2431–2432.
7. Brown T., De Carvaljo E. Practical Guide to the MIMO Radio. Wiley. 2012. P. 159–160.