Содержание
- Введение
- 1. Цель и объект исследования разработки
- 2. Обзор исследований и разработок
- 2.1 Обзор международных источников
- 2.2 Обзор национальных источников
- 3. Синтез системы автоматического регулирования натяжения стальной полосы
- 3.1 Разработка математической модели объекта управления
- 3.2 Разработка структурной схемы электропривода моталки
- 3.3 Анализ динамики САР натяжения стальной полосы
- Вывод
- Список источников
Введение
Реверсивный стан холодной прокатки – это прокатная клеть, обжимающая полосу в валках давлением на нее, создаваемым нажимными устройствами, и ее натяжением, создаваемым разматывающей моталкой (до клети) и наматывающей моталкой (после клети) при заданной скорости вращения валков. Реверс валков клети и моталок позволяет повторять обжатие чередованием направления прокатки. Регулирование толщины возможно, как воздействием на давление, так и воздействием на натяжение полосы. Исходя из жестких требований к обеспечению режимов работы в реверсивных станах, имеющих высокие скорости прокатки, жесткие технические требования, а также требования к качеству итогового материала, требуется вести непрерывный контроль за протеканием процессов проката металла и разработку более современных решений для удовлетворения условий режима работы. Применение классических схем управления не всегда удовлетворяет требования к прокату, это связанно с не всегда точной настройкой регуляторов, высокой сложностью объекта регулирования, увеличением контуров регулирования, которые ведут к ухудшению показателей помехоустойчивости и быстродействия, невозможностью автоматической перенастройки регуляторов при изменении режимов работы. Возникновение упругих деформаций в клети влечет за собой изменение давления металла на валки, а, следовательно, и влияет на величину зазора между ними, что и приводит к появлению продольной разнотолщинности листа. В настоящее время требования к точности прокатки составляют не более ±(0,025–0,05) мм от требуемой толщины полосы. Таким образом, проблема обеспечения заданной толщины полосы является достаточно актуальной.
Изображение процесса прокатки рабочего тела
(Анимированная картинка, количество циклов – 6, количество кадров – 5, размер – 9.2 Кб)
1. Цель и объект исследования разработки
Цель разработки – стабилизация реверсивной прокатки за счёт САУ компенсирующей флуктуаций натяжения рабочего тела на входе и выходе из клети.
Объект разработки – система автоматического регулирования натяжения стальной полосы в условиях одноклетьевого реверсивного стана холодной прокатки.
2. Обзор исследований и разработок
Возникновение упругих деформаций в клети влечет за собой изменение давления металла на валки, а, следовательно, и влияет на величину зазора между ними, что и приводит к появлению продольной разнотолщинности листа. В настоящее время требования к точности прокатки составляют не более ±(0,025–0,05) мм от требуемой толщины полосы. Таким образом, проблема обеспечения заданной толщины полосы является достаточно актуальной.
2.1 Обзор международных источников
Рассмотрим существующий способ регулирования натяжения полосы (рис.2.1).
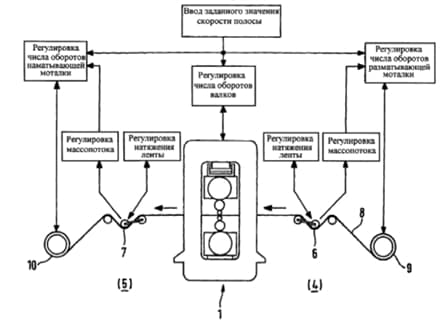
Рисунок 2.1–Схема регулирования натяжения полосы и масспотоков при помощи подвижных роликов
В данном способе предложен прокатный стан для холодной прокатки металлической полосы, в частности из стали, с прокатной клетью и средствами для установки зазора между валками. Также представлены моталки для разматывания и сматывания полосы расположенные до и после прокатной клети соответственно, отличающиеся тем, что между моталкой для разматывания полосы и прокатной клетью расположен накопитель полосы для регулирования натяжения полосы в процессе прокатки с постоянно изменяющейся по заранее заданному профилю толщины полосы, при этом накопитель выполнен в виде подвижного ролика, установленного с возможностью регулирования его положения регулятором усилия его приводного устройства с учётом заданного значения усилия получаемого исходя из измеряемого на подвижном ролике действительного значения его углового смещения и заранее заданного значения натяжной полосы, а также дополнительно с учётом заданного профиля изменения толщины полосы.
Исходя из выше перечисленного можно предложить, чтобы между моталкой расположенной перед отдельной прокатной клетью для холодной прокатки и самой отдельной прокатной клетью находился накопитель полосы, предназначенный для регулирования массопотока и регулирования натяжения в процессе прокатки.
За счёт накопителя полосы, расположенного по направлению движения полосы перед отдельной прокатной клетью, компенсируется изменения массопотока или изменения скорости движения полосы, вызванные изменениями толщины полосы или профиля толщины т.е. формы кривой изменения толщины полосы.
Таким образом, существующая система имеет ряд недостатков, а именно:
- недостаточно высокое качество продукта;
- не соответствие скоростей моталок на входе и выходе из клети;
- большая инерционность системы, т.е. низкая точность и надежность управления процессом прокатки;
- длительное проведение процесса прокатки полосы.
2.2 Обзор национальных источников
Когда положение Sʼ поршня 6 изменяется как показано на рис.2.2, для регулирования толщины проката в прокатном стане, натяжение, приложенное на рабочее тело, на входной и выходной сторонах начинают флуктуировать.
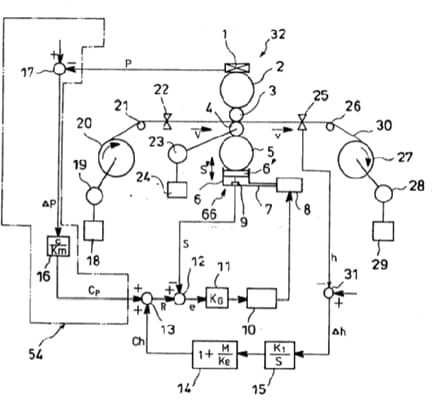
Рисунок 2.2–Общее устройство классической САРТ реверсивного прокатного стана
Если зазор между рабочими валками уменьшается, что приводит к уменьшению толщины проката, рабочее тело начнёт удлиняться и натяжение на входной и выходной сторонах будет уменьшаться. Такие флуктуации натяжений может быть поглощено за счёт изменения скоростей моталок, но они имеют большую инерцию и такое поглощение несколько медленнее чем использование регулирования зазора между рабочими валками с помощью гидронажимной системы. Результатом снижения натяжений на входной и выходной частях является увеличение деформационного сопротивления рабочего тела, что сводит на нет уменьшение зазора между рабочими валками, т.е., толщина проката не уменьшается. Иными словами, уменьшая толщину рабочего тела с помощью высокоскоростной гидронажимной системы, она не может уменьшаться быстрее, чем изменение скорости моталок.
3.Синтез системы автоматического регулирования натяжения стальной полосы
В разделе синтеза в качестве объекта управления необходимо рассмотреть регулятор натяжения рабочего тела в промежутках между моталкой и реверсивной клетью. Так как именно он должен компенсировать флуктуации натяжения стальной полосы, возникающие из-за вариаций толщины рабочего тела, которые вызывают дисбаланс скорости прокатки ΔV на входной и выходной сторонах стана.
3.1 Разработка математической модели объекта управления
При разработке концепции построения системы (рис.2.1) было выявлено, что регулятор натяжения, служит для того, чтобы изменить модуль Юнга рабочего тела, поэтому он отклоняет резонансную частоту wn, вызываемую инерционностью моталки и коэффициентом упругости (модулем Юнга) рабочего тела в область, где они не оказывают влияния на систему регулирования. Еще раз повторим структурную схему регулятора натяжения (рис.3.1).
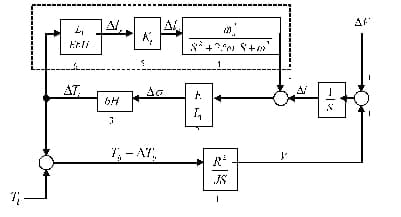
Рисунок 3.1–Структурная модель рабочего тела в МК–промежутке
Получим аналитическую модель объекта управления по структурной схеме регулятора натяжения (рис.3.1). Данная модель отражает зависимость изменения натяжения рабочего тела в продольном направлении от возможного изменения скорости прокатки. По структуре рис.3.1, не учитывая пока динамику регулятора натяжения, запишем выражение в терминах преобразования Лапласа для изменения натяжения:
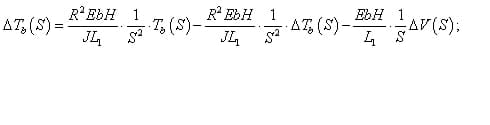
где E – модуль Юнга рабочего тела; b – ширина рабочего тела; H – толщина рабочего тела; L1 – расстояние между рабочей клетью и моталкой; J – момент инерции моталки вместе с катушкой; R – радиус катушки; S – оператор Лапласа; ΔV – изменение скорости прокатки; ΔTb – обратное изменение натяжения.
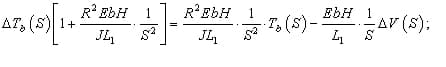
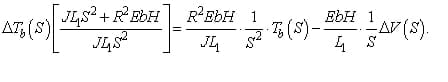
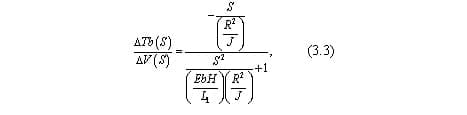
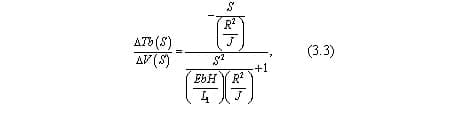
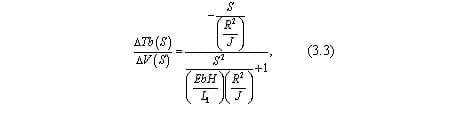
Выражая ΔTb(S), получим решение в операторной форме для изменения натяжения между моталкой и клетью относительно требуемого задания ΔTb(S) и возмущающего воздействия от скорости прокатки ΔV(S):
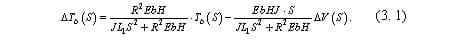
Таким образом, передаточная функция объекта по каналу возмущения «изменение натяжения рабочего тела – изменение скорости рабочего тела имеет вид:
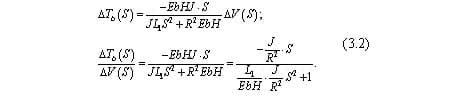
Из выражения (3.2) следует, что динамика по возмущению носит колебательный характер. С целью получения выражения для собственной частоты колебаний объекта, перепишем (3.2) следующим образом, учитывая, что частота есть обратная величина постоянной времени, тогда:
Отсюда получим собственную частоту колебаний, помня о том, что при квадрате оператора Лапласа стоит значение постоянной времени также в квадрате:
Из (3.4) следует, что собственная частота колебаний определяется конструкционными параметрами и может быть вычислена. Рассуждая аналогичным образом, получим передаточную функцию системы с блоками внутри области, отмеченной пунктирной линией (то есть с учётом системы регулирования):
Тогда аналогично, из выражения (3.4) получим выражение для резонансной частоты:
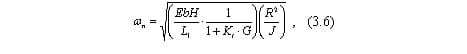
где
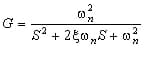
динамическая характеристика регулятора натяжения. Из (3.5) следует, что правильно подобранное значение коэффициента усиления регулятора натяжения Kt(S) может устранить явление зависимости натяжения от резонанса моталки. Тогда толщина проката не будет изменяться, даже если зазор между рабочими валками изменяется с большой частотой, как это получается в традиционных известных системах регулирования.
Докажем состоятельность модели методами математического моделирования. При моделировании объекта значения конструктивно-технологических параметров следующие:
- b – ширина рабочего тела 1800 мм;
- H – толщина рабочего тела на входе 0,52 мм, на выходе 0,3 мм;
- L1 – расстояние между рабочей клетью и моталкой 0,5 мм;
- J – момент инерции моталки вместе с катушкой, 500 кг м2;
- R – радиус катушки, 0,25м;
- V – скорость прокатки, 20…30 м/с;
- Tb – натяжение рабочего тела, 1020 Кгс=10000 Н.
Численное значение собственной частоты колебаний определим по формуле
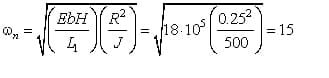
Анализ динамики объекта, а соответственно и состоятельности модели будем проводить в результате моделирования схемы приведенной на рис.3.2. На схеме скорость прокатки, т.е. скорость рабочего тела задается ступенчатым набросом с возможным ее изменением в момент времени 5 с.
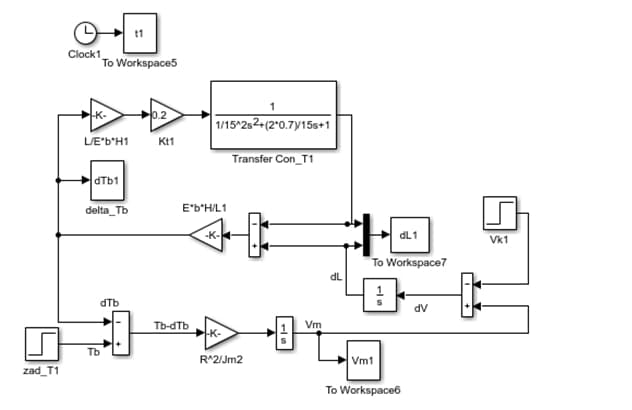
Рисунок 3.2–Схема моделирования регулятора натяжения
Скорость моталки Vm возмущается изменением скорости ΔV рабочего тела из-за возможного изменения натяжения на входной и выходной сторонах стана и / или из-за вариаций толщины рабочего тела, которые вызывают дисбаланс скорости через сумматор. Переходные процессы скорости моталки при различных значениях коэффициента усиления регулятора натяжения Kt приведены на рис.3.3. Из графиков видно, что коэффициент Kt варьируется в пределах от 0,2 до 1, изменяя переходные процессы скорости моталки от колебательного до апериодического.
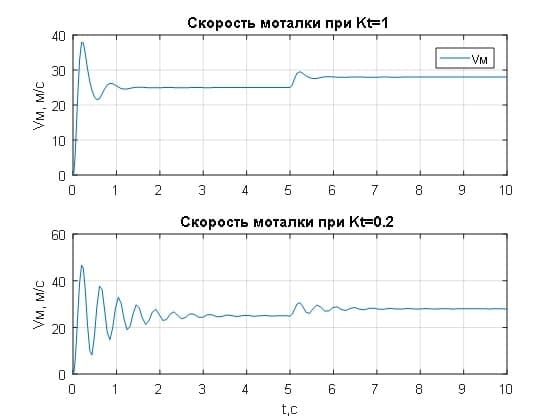
Рисунок 3.3–Переходные характеристики скорости моталки при различных значениях коэффициента регулятора натяжения
Значение ΔV интегрируется в разницу удлинений Δl в продольном направлении рабочего тела, переходные характеристики которых приведены на рис.3.4. С целью доказательства работоспособности концепции управления, разрабатываемой в бакалаврской работе, на рис.3.4. специально приведены переходные процессы удлинений рабочего тела без регулятора натяжения и с регулятором при различных значениях его коэффициента усиления. Без регулятора натяжения переходной процесс удлинений, а соответственно и изменения натяжения рабочего тела (рис.3.5) носит колебательный характер, что свидетельствует о большой инерционности моталки, которая управляется отклонением натяжения от требуемого значения ΔTb так, чтобы скомпенсировать влияние ΔV. И происходит эта компенсация очень медленно (рис.3.4 и 3.5 красным цветом).
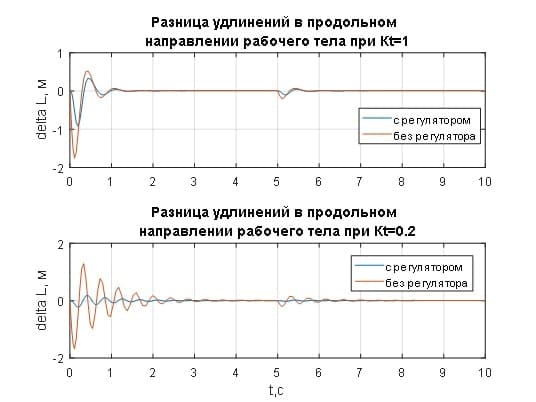
Рисунок 3.4–Переходные характеристики разницы удлинений рабочего тела при различных значениях коэффициента регулятора натяжения
Изменение натяжения ΔTb конвертируется в изменение удлинения Δlr (рис.3.2). Полученное значение усиливается в Kt раз для получения величины Δlc, с помощью которой и происходит регулирование натяжения. Таким образом, переходный процесс происходит намного быстрее, так как на него не влияет инерционность моталки (рис.3.4 и 3.5 синим цветом).
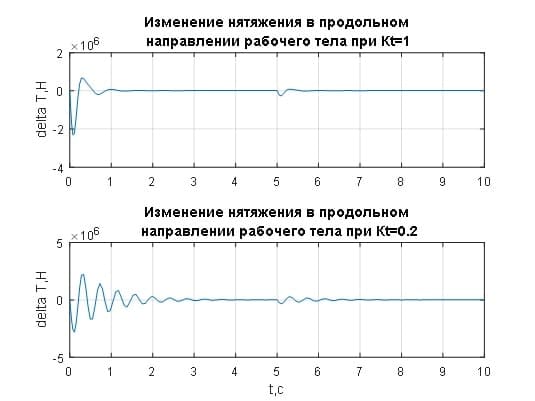
Рисунок 3.5– Переходные процессы изменения натяжения рабочего тела при различных значениях коэффициента регулятора натяжения
Таким образом, переходные характеристики, приведенные на рис. 3.3 – рис.3.5 адекватно доказывают работоспособность метода регулирования натяжения рабочего тела между моталкой и клетью реверсивной прокатки. Подбор коэффициента усиления Kt позволяет компенсировать флуктуации натяжения рабочего тела, возникающие по объективным причинам. Фактически регулятор натяжения, служит для того, чтобы изменить модуль упругости Юнга рабочего тела, отклоняя резонансную частоту wn, вызываемую инерционностью моталки в область, где она не оказывают влияния на систему регулирования.
Итак в данном подразделе подробно был описан объект управления, которым является контур регулирования натяжения. Для полной структуры системы регулирования натяжения необходимо добавить модель электропривода моталки, обеспечивающего заданное натяжение рабочего тела в промежутке между моталкой и клетью. Данная модель будет рассмотрена в следующем подразделе.
3.2 Разработка структурной схемы электропривода моталки
Для решения задачи рассмотрим общий принцип регулирования натяжения[2-4]. Момент двигателя r необходимый для создания натяжения T на катушке моталки с радиусом R, равен:
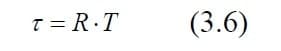
С другой стороны, выходной момент двигателя моталок равен:

Из (3.6) и (3.7), получим:
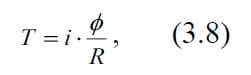
где i – ток двигателя, Φ – поле магнитной индукции двигателя.Если регулирование устроено так, что радиус катушки R становится пропорционален полю магнитной индукции Φ, то Φ/R принимает постоянное значение и натяжение T становится пропорционально току двигателя i.
При разработке математической модели унифицированного электропривода (ЭПУ) постоянного тока, необходимо учесть, что структура его управления трехконтурная с принципом подчиненного регулирования
[5-10]. Это означает, что внешним контуром является контур регулирования натяжения, который устанавливает задание на внутренний контур – регулятор скорости вращения двигателя моталки, который, в свою очередь корректирует и ограничивает задание на контур регулятора тока якоря двигателя моталки. Такие структуры подчиненного регулирования реализованы в стандартных унифицированных ЭПУ.
Математическую модель трехконтурной САУ электроприводом моталки можно представить в виде системы интегро–дифференциальных уравнений(3.9):

Здесь известными функциями времени являются: UIm(t) – управляющее воздействие (ЭДС источника питания электродвигателя) (B), регулируемое по ПИ–закону управления [5-10]; Uw(t),UTb(t) – управляющие воздействия для контуров управления скорости вращения моталки и натяжения рабочего тела, соответственно, регулируемые по ПИ–закону управления [5-10].
Mc(t) – возмущающее воздействие (момент собственной нагрузки электропривода, т.е. сопротивление деформации рабочего тела в очаге деформации, приведенное к ротору двигателя) (H*m ).
Известными также являются параметры системы:
Неизвестными в этой системе являются: w – скорость вращения двигателя (рад/с); I – ток якоря (A) , соответствующий электромагнитному моменту MЭМ=C*I, (H*m); Tb– натяжение моталки (H).
На рис.3.6 приведена схема моделирования САУ ЭПУ моталки, основанная на системе интегродифференциальных уравнений (3.9).
Параметры унифицированного ЭПУ, которые необходимы для расчета коэффициентов передачи и постоянных времени двигателя следующие:
- номинальная мощность 67 КВт;
- номинальная частота вращения 1500 об/мин;
- номинальное напряжение 600 В;
- номинальный вращающий момент 426,5 Нм;
- номинальный ток якоря 117,5 А;
- индуктивность силовых цепей ТП-Д 0,001 Гн;
- активное сопротивление силовых цепей ТП–Д 0,01 Ом.
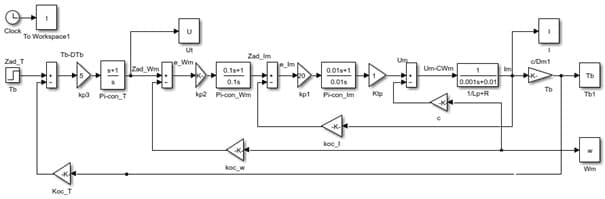
Рисунок 3.6– Схема моделирования ЭПУ моталки
3.3 Анализ динамики САР натяжения стальной полосы
Анализ динамических процессов в системе автоматического регулирования натяжения рабочего тела между моталкой и реверсивной клетью будем проводить в результате моделиривования полной схемы, включающей модель ЭПУ моталки и регулятора натяжения. Данная схема моделирования приведена на рис.3.7.
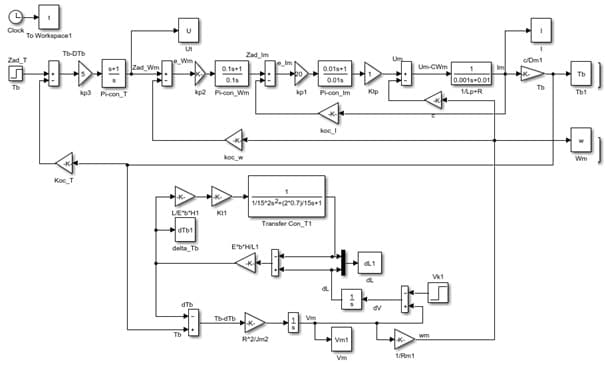
Рисунок 3.7– Схема моделирования САР натяжения стальной полосы
Проанализируем переходные процессы в САР. На рис.3.8 приведены переходные процессы ЭПУ моталки при коэффициенте усиления регулятора натяжения, равного 0,1.
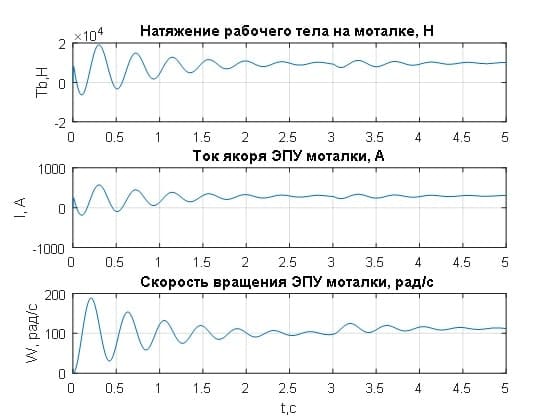
Рисунок 3.8– Переходные процессы в системе ЭПУ моталки при коэффициенте регулятора натяжения Kt=0.1
Из графиков видно, что процессы по основным регулируемым переменным носят колебательный характер и до момента изменения скорости прокатки в 3 с не устанавливаются. Скорость моталки также имеет динамику колебаний (рис.3.9). Изменения натяжения, вызванные возмущением скорости прокатки, свидетельствуют о том, что моталка не справляется с компенсацией изменения скорости прокатки даже с 25 м/с до 28 м/с (рис.3.10) в силу своей большой инерционности.
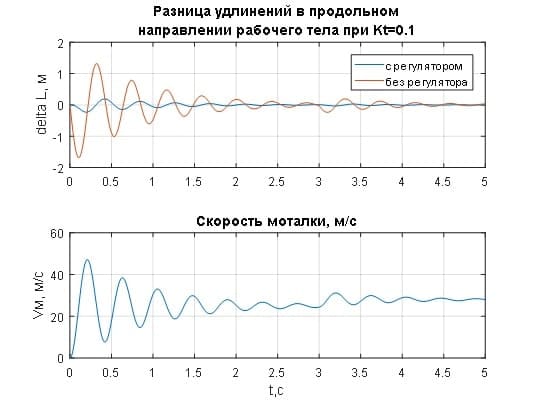
Рисунок 3.9– Переходные характеристики разницы удлинений рабочего тела при Kt=0.1
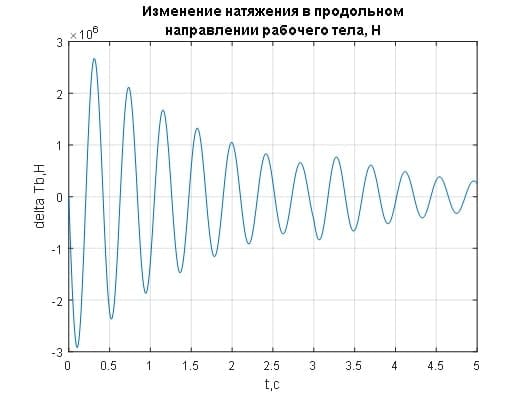
Рисунок 3.10– Переходные процессы изменения натяжения рабочего тела при Kt=0.1
С целью возможности быстрой компенсации возникающих флуктуаций натяжений стальной полосы, скорректируем коэффициент регулятора моталки Kt, который даже при наличии инерции моталки обеспечит хороший результат, за счет отклонения резонансной частоты wn, вызываемой инерционностью моталки в область, где она не оказывают влияния на систему регулирования.
Переходные процессы по основным регулируемым переменным ЭПУ имеют апериодический характер (рис.3.11), время регулирования 0,8 с, что является хорошим показателем для объектов данного класса [10]. Отработка изменения скорости прокатки происходит за 0,25 с.
Переходные процессы удлинения и изменения натяжения рабочего тела вдоль оси прокатки свидетельствуют о том, что флуктуации натяжения полосы при изменении скорости прокатки компенсируются в течении 0,5 с (рис.3.12, рис.3.13).
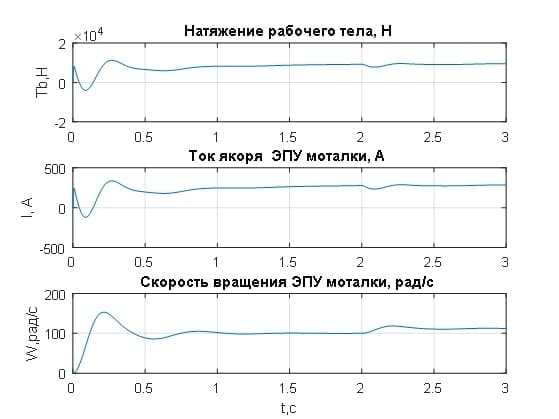
Рисунок 3.11– Переходные процессы в системе ЭПУ моталки при коэффициенте регулятора натяжения при Kt=1
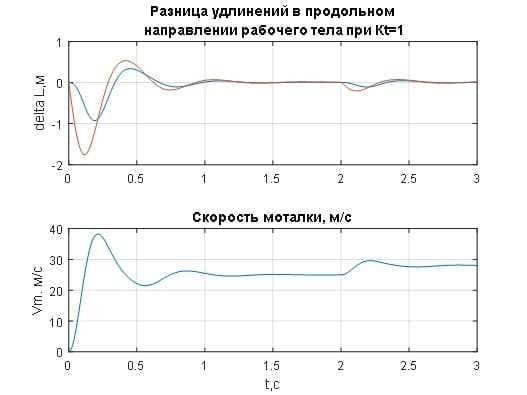
Рисунок 3.12– Переходные процессы в системе ЭПУ моталки при коэффициенте регулятора натяжения при Kt=1
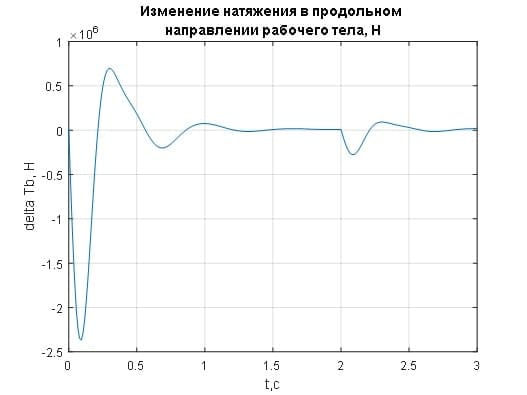
Рисунок 3.13– Переходные процессы изменения натяжения рабочего тела при Kt=1
Таким образом, анализ динамических процессов в САР натяжения стальной полосы доказал работоспособность предложенной концепции управления. Практика исследования и моделирования схемы рис. 3.7 показала, что численное значение коэффициента усиления регулятора натяжения в данных технологических условиях реверсивной прокатки, дающее удовлетворительные результаты по быстродействию САР лежит в пределах от 0,5 до 1 ед.
Вывод
- Получена математическая модель регулятора натяжения, позволяющая компенсировать флуктуации натяжения рабочего тела, вызванные изменением скорости рабочего тела из-за изменения натяжения на входной и выходной сторонах стана и/или из–за вариаций толщины рабочего тела. Фактически регулятор натяжения, служит для того, чтобы изменить модуль упругости Юнга рабочего тела, отклоняя резонансную частоту, вызываемую инерционностью моталки в область, где она не оказывают влияния на систему регулирования.
- Получена математическая модель САУ ЭПУ моталки, представляющая собой трехконтурную систему с подчиненным регулированием. Данная модель позволила выполнить анализ динамических процессов по основным регулируемым переменным электропривода моталки.
- Выполнен анализ динамики САР натяжения стальной полосы по общей структуре системы, включающей систему ЭПУ моталки и регулятор натяжения. Анализ переходных процессов в САР натяжения доказал работоспособность регулятора натяжения. Переходные процессы по основным регулируемым переменным имеют показатели качества регулирования, соответствующие требованиям предъявляемым к объектам данного класса. Время регулирования 0,75 с, отработка возмущения 0,5 с.
Список источников
- Дружинин Н.Н. Непрерывные станы, как объект автоматизации. — М.: Металлургия, 1975. — 336 с.
- Выдрин В.Н., Федосиенко А.С. Автоматизация прокатного производства. — М.: Металлургия, 1984 — 472 с.
- Кузнецов Б.И., И.О. Опришко, И.М. Богаенко и др. Автоматизация управления листовыми прокатными станами. — К.: Техника, 1992. — 231 с.
- Гудвин Г.К., Гребе С.Ф., Сальгадо М.Э., Проектирование систем управления, 2004г — 962 с.
- Афанасьев В.С. Автоматизированный электропривод в прокатном производстве: Уч. для вузов. — М.: Металлургия, 1977. — 280 с.
- Комплектные тиристорные электроприводы: Справочник /Под. ред. В.М. Перельмутера. — М.: Энергоатомиздат, 1988. — 319 с.
- Перельмутер В.М., Сидоренко В.А. Системы управления тиристорным электроприводом постоянного тока. М.: Энергоатомиздат, 1988.
- Башарин А.В., Новиков В.А., Соколовский Г.Г. Управление электроприводами: Учебное пособие для вузов. — Л.: Энергоатомиздат. Ленинградское отделение, 1982. — 392 с.
- Ключев В.И. Теория электропривода: Учебное пособие для вузов., 2—е изд. перераб. и доп. — Л.: Энергоатомиздат, 1998. — 704 с.
- Дралюк Б.Н., Конторович Б.И., Маланов А.Л.// Электропривод и автоматизация мощных машин: Сб. науч. тр. — Свердловск: НИИтяжмаш, 1991г. С.81—96.
- Дралюк Б.Н., Конторович Б.И., Маланов А.Л.// Внедрение микропроцессорной САРТ на реверсивном стане холодной прокатки. Изд. "Металлургия", "Сталь" N 5, 1996, с.33—36.
- 7. Тиристорные электропривода прокатных станов /В.М. Перельмутер, Ю.Н. Брауде, Д.Я. Перчик, В.М. Книгин /Под ред. В.М. Перельмутера. – М.: Металлургия, 1978. — 151 с.
