Классификация нейронных сетей

Аннотация

Горбачевская Е. Н. Классификация нейронных сетей Классификация нейронных сетей по видам решаемых задач, по видам используемых нейронов, по структуре связей нейронов, способам обучения нейронной сети.

При решении задач с использованием нейронной сети подбирают стандартную конфигурацию нейросети, но с учетом сложности и особенности задачи подбор существующих конфигураций может быть проблематичен. Если же задача не может быть сведена ни к одному из известных типов нейросети, приходится решать сложную проблему синтеза новой конфигурации.

Для определения структуры модели нейронной сети необходимо решить несколько задач: построить классификацию нейронных сетей; провести анализ существующих нейронных сетей; разработать основные критерии отбора нейронных сетей для построения модели; определить основные характеристики для определения качества модели на основе нейронной сети.

Гипотеза исследования: подробная классификация нейронных сетей позволит выявить основные характеристики нейронных сетей и критерии отбора существующих моделей.

Методологической основой исследования явились общенаучные принципы проектирования, теория системно–комплексных подходов к построению классификации.

В исследовании использовались работы по описанию и классификации нейронных сетей: В. В. Круглова, В. В. Борисова, И. Г. Сидоркиной, В. А. Терехова, Л. Н. Ясницкого и др.

Для решения поставленных в исследовании задач применялись следующие методы: анализ литературы по проблеме исследования, технической документации; обобщение опыта отечественной и зарубежной практики построения нейронных сетей.

Основной характеристикой нейронной сети является модель сети. Охарактеризовать нейронные сети можно по видам нейронов используемых в сети, структуры модели сети, способам обучения сети, задачам которые решает сеть. Рассматривая задачи решаемые нейронными сетями можно выделить широкий круг задач обработки и анализа данных – распознавание и классификация образов, прогнозирование, управление, кластерный анализ, аппроксимация, нейросетевое сжатие данных, ассоциативную память и т. д.

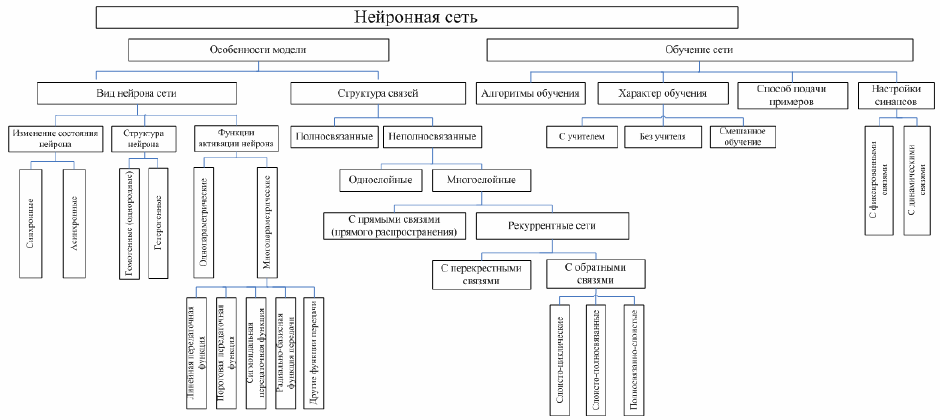
По структуре связей нейронные сети можно разделить на (рисунок 1):

1. Монотонные. Это частный случай слоистых сетей с дополнительными условиями на связи и нейроны. Каждый слой кроме последнего (выходного) разбит на два блока: возбуждающий и тормозящий. Связи между блоками тоже разделяются на тормозящие и возбуждающие. Если от нейронов блока А к нейронам блока В ведут только возбуждающие связи, то это означает, что любой выходной сигнал блока является монотонной неубывающей функцией любого выходного сигнала блока А. Если же эти связи только тормозящие, то любой выходной сигнал блока В является невозрастающей функцией любого выходного сигнала блока А. Для нейронов монотонных сетей необходима монотонная зависимость выходного сигнала нейрона от параметров входных сигналов.
2. Сети без обратных связей. В таких сетях нейроны входного слоя получают входные сигналы, преобразуют их и передают нейронам первого скрытого слоя, и так далее вплоть до выходного, который выдает сигналы для интерпретатора и пользователя. Если не оговорено противное, то каждый выходной сигнал q–гo слоя подастся на вход всех нейронов (q+1)–гo слоя; однако возможен вариант соединения q–гo слоя с произвольным (q+p)–м слоем.
3. Сети с обратными связями. В сетях с обратными связями информация с последующих слоев передается на предыдущие. Среди них, в свою очередь, выделяют следующие:
• слоисто–циклические, отличающиеся тем, что слои замкнуты в кольцо: последний слой передает свои выходные сигналы первому; все слои равноправны и могут как получать входные сигналы, так и выдавать выходные;
• слоисто–полносвязанные состоят из слоев, каждый из которых представляет собой полносвязную сеть, а сигналы передаются как от слоя к слою, так и внутри слоя; в каждом слое цикл работы распадается на три части: прием сигналов с предыдущего слоя, обмен сигналами внутри слоя, выработка выходного сигнала и передача к последующему слою;
• полносвязанно–слоистые, по своей структуре аналогичные слоисто–полносвязанным, но функционирующим по–другому: в них не разделяются фазы обмена внутри слоя и передачи следующему, на каждом такте нейроны всех слоев принимают сигналы от нейронов как своего слоя, так и последующих.

Известные нейронные сети можно разделить по типам структур нейронов на:

гомогенные (однородные);

гетерогенные.

Гомогенные сети состоят из нейронов одного типа с единой функцией активации, а в гетерогенную сеть входят нейроны с различными функциями активации.

Активационная функция нейрона определяет нелинейное преобразование осуществляемое нейроном [2]. Существует множество активационных функций. Самые распространенные из них:

1. Линейная передаточная функция;
2. Пороговая передаточная функция;
3. Сигмоидальная передаточная функция (логистическая функция, гиперболический тангенс и др.);
4. Радиально-базисная функция передачи;
5. Другие функции передачи.

При линейной передаточной функция сигнал на выходе нейрона линейно связан со взвешенной суммой сигналов на его входе.

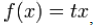
где t – параметр функции. В искусственных нейронных сетях со слоистой структурой нейроны с передаточными функциями такого типа, как правило, составляют входной слой. Кроме простой линейной функции могут быть использованы её модификации. Например полулинейная функция (если её аргумент меньше нуля, то она равна нулю, а в остальных случаях, ведет себя как линейная) или шаговая (линейная функция с насыщением), которую можно выразить формулой:

Пороговая передаточная функция (Функция Хевисайда) представляет собой перепад. До тех пор пока взвешенный сигнал на входе нейрона не достигает некоторого уровня – сигнал на выходе равен нулю. Как только сигнал на входе нейрона превышает указанный уровень – выходной сигнал скачкообразно изменяется на единицу. Математическая запись этой функции выглядит так:

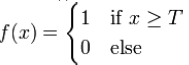
Здесь T=-w₀x₀ – сдвиг функции активации относительно горизонтальной оси, соответственно под следует понимать взвешенную сумму сигналов на входах нейрона без учёта этого слагаемого. Ввиду того, что данная функция не является дифференцируемой на всей оси абсцисс, её нельзя использовать в сетях, обучающихся по алгоритму обратного распространения ошибки и другим алгоритмам, требующим дифференцируемости передаточной функции.

Сигмоидальная передаточная функция &ndash один из самых часто используемых, на данный момент, типов передаточных функций. Введение функций сигмоидального типа было обусловлено ограниченностью нейронных сетей с пороговой функцией активации нейронов &ndash при такой функции активации любой из выходов сети равен либо нулю, либо единице, что ограничивает использование сетей не в задачах классификации. Использование сигмоидальных функций позволило перейти от бинарных выходов нейрона к аналоговым [1]. Функции передачи такого типа, как правило, присущи нейронам, находящимся во внутренних слоях нейронной сети.

Логистическую функцию математически можно выразить как:

Здесь t – это параметр функции, определяющий её крутизну. Когда t стремится к бесконечности, функция вырождается в пороговую. При t=0 сигмоида вырождается в постоянную функцию со значением 0,5. Область значений данной функции находится в интервале (0,1). Важным достоинством этой функции является простота её производной:

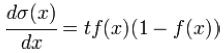
То, что производная этой функции может быть выражена через её значение облегчает использование этой функции при обучении сети по алгоритму обратного распространения. Особенностью нейронов с такой передаточной характеристикой является то, что они усиливают сильные сигналы существенно меньше, чем слабые, поскольку области сильных сигналов соответствуют пологим участкам характеристики. Это позволяет предотвратить насыщение от больших сигналов.

Использование функции гиперболического тангенса:

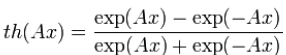
отличается от рассмотренной выше логистической кривой тем, что его область значений лежит в интервале (-1;1). Т. к. верно соотношение:

то оба графика отличаются лишь масштабом осей. Производная гиперболического тангенса, разумеется, тоже выражается квадратичной функцией значения; свойство противостоять насыщению имеет место точно также.

Радиально–базисная функция передачи принимает в качестве аргумента расстояние между входным вектором и некоторым наперед заданным центром активационной функции. Значение этой функции тем выше, чем ближе входной вектор к центру [3]. Сети с нейронами, использующими такие функции, называются RBF–сетями.

В реальных сетях активационная функция нейронов может отражать распределение вероятности какой-либо случайной величины, либо обозначать какие-либо эвристические зависимости между величинами.

Перечисленные выше функции составляют лишь часть от множества передаточных функций, используемых на данный момент. В число других передаточных функций входят такие как: экспонента 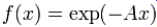; тригонометрический синус; модульная: ; квадратичная.

Еще одна классификация делит нейронные сети на:

синхронные;

асинхронные.

В первом случае в каждый момент времени лишь один нейрон меняет свое состояние, во втором – состояние меняется сразу у целой группы нейронов, как правило, у всего слоя. Алгоритмически ход времени в нейронных сетях задается итерационным выполнением однотипных действий над нейронами [1].

При классификации по характеру настройки синапсов можно выделить сети с фиксированными связями (весовые коэффициенты нейронной сети выбираются сразу, исходя из условий задачи, при этом: 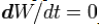, где W – весовые коэффициенты сети) и сети с динамическими связями (для них в процессе обучения происходит настройка синаптических связей, то есть 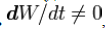, где W – весовые коэффициенты сети).

По организации обучения разделяют обучение нейронных сетей:

с учителем (supervised neural networks);

без учителя (nonsupervised);

смешанное обучение.

При обучении с учителем предполагается, что есть внешняя среда, которая предоставляет обучающие примеры (значения входов и соответствующие им значения выходов) на этапе обучения или оценивает правильность функционирования нейронной сети и в соответствии со своими критериями меняет состояние нейронной сети или поощряет (наказывает) нейронную сеть, запуская тем самым механизм изменения ее состояния.

Определяют так же различные алгоритмы обучения:

по входам;

по выходам.

При обучении по входам обучающий пример представляет собой только вектор входных сигналов, а при обучении по выходам в него входит и вектор выходных сигналов, соответствующий входному вектору.

По способу предъявления примеров различают:

предъявление одиночных примеров;

предъявление страницы примеров.

В первом случае изменение состояния нейронной сети (обучение) происходит после предъявления каждого примера. Во втором – после предъявления страницы (множества) примеров на основе анализа сразу их всех.

В данной работе предлагается классификация нейронных сети. На основе разработанной классификации можно сделать вывод, что основой проектирования или выбора модели нейронной сети для поставленной задачи, является структура связей между слоями нейронов, вид нейронов (с точки зрения передаточной функции), правила определения весовых коэффициентов при обучении нейронной модели.

Список использованной литературы

1. В. В. Круглов, В. В. Борисов – Искусственные нейронные сети Теория искусственных нейронных сетей.
2. В. В. Круглов, В. В. Борисов – Искусственные нейронные сети. Теория и практика
3. Л. Н Ясницкий – Введение в искусственный интеллект.