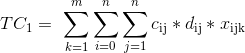
Сяолей Лян1*, Юань Сунь1, Мендан Тянь1, Вэньфэн Чжоу11 Школа автомобильной и транспортной инженерии, Уханьский университет науки и Технология, Ухань, Хубэй, 430081, Китай
* Адрес электронной почты автора: liangxiaolei@wust.edu.cn
Аннотация: Чтобы применить алгоритмы роевого интеллекта для решения проблемы маршрутизации транспортных средств холодной цепи эффективно и удобно, был предложен упрощенный метод расшифровки. Основываясь на общей форме кодирования в непрерывном пространстве для алгоритмов роевого интеллекта, процесс расшифровки был разделен на три части: расшифровка последовательности обслуживания клиентов, назначение клиента и определение маршрута каждого транспортного средства, круговой расчет и вывод всей схемы. Нет необходимости разрабатывать новую форму кодирования для эффективного решения проблемы. Были проведены эксперименты на двух примерах с использованием выведенной метода расшифровки внедренного в 9 различных алгоритмов для проверки его производительности. Результаты показали, что этот метод может быть использован в алгоритмах роевого интеллекта для решения проблемы маршрутизации транспортных средств холодной цепи. Кроме того можно заметить, что разные алгоритмы показали разные характеристики из-за своих механизмов поиска, хотя они были основаны на одном и том же методе декодирования.
Автор перевода: Хубеджев Д.П.
1. Введение
Логистика холодной цепи развивалась на протяжении 80 лет для формирования ее современной системы. Сюй [1] и Кейзер [2] рассматривают такие факторы влияния, как скоропортящийся продукт и энергопотребление продуктов, и предоставляют модель для снижения стоимости транспортировки. Основываясь на анализе проблем временного ограничения и планирования производства скоропортящихся продуктов. Чен [3] и его соавторы построили нелинейную математическую модель и ввели гибридный алгоритм, сочетающий метод Нелдера-Мида и эвристический алгоритм, для ее решения. Куо [4] и его соавторы предложили модель мультитемпературного распределения, основанную на степени воздействия температуры на скоропортящиеся продукты. Рассматривая характеристики скоропортящихся пищевых продуктов, Ши и Фу [5] ввели изменяющийся во времени фактор распределительной сети для исследования местоположения распределения и оптимизации пути транспортировки, и построили имитационную модель в изменяющихся во времени условиях.
Хотя некоторые алгоритмы роевого интеллекта были применены для решения проблемы, их метод кодирования является сложным и неэффективным. Таким образом, в этой статье предлагается упрощенный метод расшифровки, который сохраняет основной режим кодирования, но вводит эвристический метод для реализации назначения клиента и графика транспортного средства для логистики холодной цепи.
2. Оптимизация модели маршрутизации транспортных средств для распределения по технологии холодной цепи.
2.1 Вступление
2.1.1 Стоимость транспортировки
Процесс логистической дистрибуции холодной цепи заключается в том, что продукты доставляются из центра логистической дистрибуции покупателям на рефрижераторных транспортных средствах. Предполагается, что спрос каждого клиента и местоположение заданы. Кроме того, существует ограничение по времени на время доставки клиенту. Товары могут быть доставлены немедленно, если время прибытия транспортного средства находится в пределах временного интервала. Если нет, они также могут быть доставлены, но штраф должен быть оплачен. Задача состоит в том, чтобы создать экономичный план распределения транспортных средств, для минимизации общей стоимости.
2.1.2 Определение параметров
На основе теории графов логистическая сеть холодной цепи может быть определена как: G=(V, D), где V=(v0, v1, v2, …, vn) это набор точек дистрибуции и клиентов. v0 представляет центр дистрибуции, а vi (i=1, 2, 3, …, n) представляет i-того клиента.
D=((vi, vj): vi, vj) — множество всех отрезков пути.
m: количество транспортных средств доставки, доступных в центре распределения;
N: общее количество клиентов;
fk: фиксированная стоимость k-го транспортного средства;
Qk: максимальная грузоподъемность k-го транспортного средства;
cij: стоимость перевозки автомобиля на участке дороги (vi,vj);
xijk: если k-й автомобиль проходит путь (vi, vj), xijk = 1, в противном случае xijk = 0;
yijk: если k-й автомобиль обслуживает клиента i, yijk = 1, в противном случае yijk = 0;
dij: расстояние между клиентами i и j;
qi: спрос клиента i;
p: стоимость единицы товара;
t0t: время отправления k-го транспортного средства доставки из центра дистрибуции;
t1t: время, когда k-й автомобиль прибывает к клиенту i;
ei, li (i=1, 2, 3, …, n): границы времени доставки, в которые клиент может принять заказ;
a: штрафной коэффициент за раннее прибытие;
b: штрафной коэффициент за задержку прибытия.
2.2. Математическая модель
2.2.1. Стоимость транспортировки
В процессе логистического распределения холодной цепи, транспортные расходы и удовлетворенность клиентов являются основными факторами, влияющими на ситуацию. Затраты на распространение, вовлеченные в это исследование, показаны следующим образом:
Стоимость транспортировки
Логистика холодных цепей предъявляет более высокие требования к транспортным средствам и холодильному оборудованию, поэтому ее транспортные расходы выше, чем у обычных транспортных средств. Как правило, транспортные расходы распределительных транспортных средств включают в себя расход топлива, расходы на техническое обслуживание, трудозатраты и т. д., которые пропорциональны расстоянию перемещения транспортного средства. Упрощенная формула, используемая в этом исследовании, показана ниже:
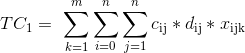 |
(1) |
Размер штрафа
В отличие от общей логистики, качество товаров более чувствительно ко времени в логистике холодной цепи. Клиенты часто имеют строгие ограничения по срокам доставки, чтобы получить более высокий доход и уровень обслуживания. Однако, в процессе фактического распространения многие неожиданные события и факторы, такие как пробки, изменения погоды, будут нарушать план распределения транспортного средства. Таким образом, время доставки продукции холодной цепи можно разделить на: раннюю доставку, своевременную доставку и задержанную доставку в зависимости от реальных ситуаций.
Ранняя доставка: когда kit ≤ e, автомобиль прибывает заранее. Прибытие заранее приведет к недостаточной подготовке клиента, поэтому необходимо заплатить определенный штраф. Коэффициент штрафа устанавливается как a;
Своевременная доставка: если время доставки l ≥ kit ≥ e, время прибытия средства доставки находится в пределах временного ограничения покупателя. Транспортное средство может выполнить свою задачу без штрафа;
Задержка доставки: когда комплект kit ≥ l, автомобиль не прибывает вовремя, что приведет к определенным потерям для клиента. Таким образом, определенный штраф должен быть оплачен. Коэффициент штрафа равен b;
объединив эти три ситуации, штраф клиента может быть выражен как:
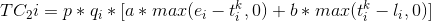 |
(2) |
Общая стоимость штрафа для всех транспортных средств выглядит следующим образом:
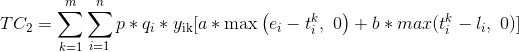 |
(3) |
Фиксированная стоимость транспортных средств
Фиксированная стоимость в основном относится к затратам на отправку каждого транспортного средства, включая потерю транспортного средства, стоимость рабочей силы и так далее. Предполагая, что имеется m транспортных средств (k = 1, 2,…, m) для обслуживания n клиентов, фиксированная стоимость k-го транспортного средства равна fk, общая фиксированная стоимость составляет:
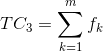 |
(4) |
2.2.2. Модель
Согласно приведенному выше анализу затрат, обобщенная функция задачи маршрутизации транспортных средств логистики холодной цепи определяется как:
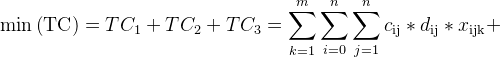  |
(5) |
|---|---|
 |
(6) |
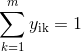 |
(7) |
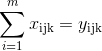 |
(8) |
 |
(9) |
Ei ≤ tik ≤ Li |
(10) |
Формула (6) представляет лимиты общей нагрузки транспортного средства; формула (7) показывает, что каждый автомобиль может одновременно обслуживать только одного клиента; формулы (8) и (9) показывают, что если транспортное средство проходит точку спроса, оно должно ее обслуживать; формула (10) указывает пределы временного ограничения.
3. Методология
3.1. Анализ поисковых характеристик алгоритмом роевого интеллекта
В процессе работы алгоритма роевого интеллекта каждый индивид представляет допустимое решение в допустимом доменном пространстве. Благодаря коллективному сотрудничеству индивиды постоянно корректируют свои позиции и обновляют информацию о возможных решениях. Оценка качества возможных решений основывается на функции пригодности или целевой функции. В рамках алгоритма роевого интеллекта глобальный поиск и локальный поиск являются двумя важными компонентами. Различные алгоритмы роевого интеллекта имеют разные механизмы поведения в глобальном поиске и локальном поиске, но вычислительная структура одинакова. Следовательно, метод кодирования универсален при использовании алгоритма разведки роя для оптимизации проблемы.
3.2 Индивидуальный метод кодирования
Модель задачи распределения холодной цепи относится к проблеме маршрутизации транспортного средства с ограничениями по пропускной способности и временному ограничению. Необходимо ограничить количество транспортных средств и маршрутов дистрибуции в соответствии с ограничениями. Задача оптимизации маршрутов дистрибуции также является задачей оптимизации дискретного пространства. Чтобы избежать изменения отдельных правил кодирования, здесь предлагается метод расшифровки с эвристическим методом для сопоставления отдельного выражения с пространством решения задачи, а затем для получения количества транспортных средств и схем маршрутизации из отдельного представления. Для индивидуальной структуры в алгоритме роевого интеллекта индивидуальное выражение все еще принимает традиционный метод кодирования непрерывного пространства. Любой индивид может быть представлен как x=(xi1, xi2, … xiD)T, где i представляет любого индивида, а D представляет количество клиентов.
На основе индивидуального выражения новый процесс расшифровки делится на три этапа:
Этап 1: Расшифровка последовательности обслуживания клиентов. Значения в каждом измерении для отдельного xi сортируются для получения упорядоченного целочисленного массива S, как показано в таблице 1. Каждый номер измерения в S представляет номер клиента, а целое число sj в каждом измерении является назначенным заказом для соответствующего клиента.
Таблица 1 Позиционная расшифровка индивидуальной информации
| xi | xi1 | xi2 | … | xij | … | xiD |
| ⇓ | ||||||
| S | s1 | s2 | … | sj | … | sD |
Этап 2: назначить клиента и определить маршрут R для каждого транспортного средства. На этом этапе, основываясь на ограничениях вместимости транспортного средства, назначение клиента выполняется в соответствии с заказом, полученным от S. Процесс описан на рисунке 1.
Этап 3: выведение плана pi. На основании результатов расшифровки следует рассчитать количество транспортных средств и порядок клиентов, обслуживаемых автомобилями. Затем вывести план.
Следует отметить, что алгоритмы роевого интеллекта, особенно те, которые ищут в непрерывном пространстве, имеют много общего в формах кодирования и поиска. Следовательно, процессы декодирования подходят для другого алгоритма роевого интеллекта с такими же характеристиками для решения этого типа проблемы.
4. Тематическое исследование
4.1 Экспериментальные установки
Чтобы проверить производительность метода кодирования, представлены два разных случая: средние проблемы с 30 клиентами и крупные проблемы с 50 клиентами. Предоставлена такая информация, как координата точки (xi, yi), ее запрос, время работы и временное границы для передачи. По данным эксплуатационной работы и опросов, данные по вышеуказанным случаям генерируются случайным образом.
Для сравнения производительности метода кодирования в различных алгоритмах для задачи оптимизации маршрутов холодной цепи выбраны девять алгоритмов роевого интеллекта. Выбранные алгоритмы и настройки показаны в Таблице 2, включая CLPSO, BBO, FA, ABC, CS, BFO, BA, SNSO и GA. Во всех экспериментах численность населения составляет 30.
| Алгоритм: Стратегия назначения клиентов с учетом ограничений по мощности |
|---|
Входные параметры: массив S, ограничение по грузоподъемности L, запрос клиента N Выходные параметры: маршрут R BEGIN
END Рисунок 1. Процесс назначение клиента с учетом ограничения по грузоподъемности |
Таблица 2. Сравнение алгоритмов и параметров
| Alg. | Parameters | Alg. | Parameters | |
|---|---|---|---|---|
CALPSO BBO FA ABC CS |
C=1.5, ωmax=0.95, ωmax=0.4, m=5 I=E=1 α=0.5, β=0.2, y=1 limit=100 Pa=0.25, α=0.5, β=3/2 | BFO BA SNSO GA |
Ne=10, Nr=10, Nc=10, Ns=10, C=0.01, Ped=0.9 α=0.9, y=0.5, r=0.5, A=0.25 PN= PR=0.2 Pc=0.9, Pm=0.01 |
4.2. Результаты и анализ
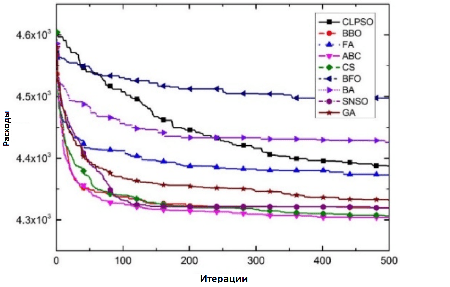
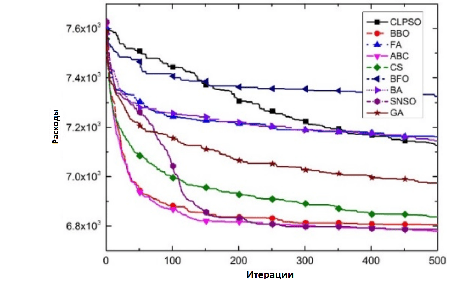
Из статистических результатов (таблица 3) видно, что точность большинства алгоритмов близка в среднем масштабе. В частности, точность и стабильность поискового решения, полученного ABC, CS, SNSO и GA, немного лучше, чем у других алгоритмов роевого интеллекта. Кривые на рисунке 2 показывают, что ABC, CS, SNSO и GA быстро сходятся на ранней стадии, что указывает на то, что эти алгоритмы обладают хорошими возможностями глобального поиска на ранней стадии и могут быстро найти оптимальный регион для его изучения.
Тем не менее, для результатов случая с большими размерностями (таблица 4) можно сделать вывод, что при увеличении масштаба задачи характеристики алгоритмов различаются. BBO, ABC и SNSO получают результаты и работают лучше, чем другие. С увеличением масштаба задач усложняется оптимизация, а также увеличивается потребность в поисковой способности алгоритмов. Сравнение кривых сходимости (рис. 3) также показывает, что алгоритмы BFO, BA и FA имеют недостаточную способность непрерывного поиска в решении этой проблемы. После некоторых этапов локального поиска на ранней стадии их популяция застаивается в средний и более поздние периоды и не может вырваться из области локального экстремума. Однако кривые сходимости BBO, ABC и SNSO продолжают снижаться. Это означает, что они могут глубоко исследовать пространство решений, что приводит к более высокой точности, по сравнению с другими алгоритмами.
Посредством вышеприведенного анализа можно сделать вывод, что схема кодирования и расшифровки, разработанная в этой статье, может быть применена для решения задачи оптимизации маршрутизации логистического распределения холодной цепи, используя алгоритмы роевого интеллекта. Большинство алгоритмов могут получить приближенное к оптимальному решение и иметь хорошую применимость.
Таблица 3. Результаты случая 1
|
Таблица 4. Результаты случая 2
|
 |  |
|
| Рисунок 2. Сравнение кривых сходимости алгоритмов в случае 1 | Рисунок 3. Сравнение кривых сходимости алгоритмов в случае 2 |
5. Вывод
В этой статье было представлено, как использовать алгоритмы роевого интеллекта для оптимизации распределения рефрижераторных транспортных средств в логистике холодной цепи. Новый метод расшифровки разработан путем объединения алгоритма роевого интеллекта с особенностями проблемы. В ходе экспериментов, включающих средние и сложные случаи, были проанализированы 9 интеллектуальных алгоритмов для решения проблемы с введенным методом. Результаты показывают, что общая модель проблемы может быть решена с использованием некоторых алгоритмов роевого интеллекта в соответствии с методом обеспечения расшифровки и работает эффективно.
Благодарность
Эта работа была частично поддержана Национальным фондом естественных наук Китая (№ 61603280), Фондом фонда для молодых учителей WUST (№ 2016xz029) и Программой обучения студентов и новаторов в провинции Хубэй (№ 201610488045).
Список литературы