
УДК 004.021
Хубеджев Д.П., Ситникова О.Д. Решение задачи логистики поставок по нескольким циклическим и радиальным маршрутам с учетом использования различных видов транспорта. В статье формализована задача поставок продукции из одного склада в сеть торговых точек с учетом возможностей транспортных средств с целью минимизации суммарной длинны всех маршрутов. Приведен алгоритм решения этой задачи, являющийся модификацией метода Кларка-Райта.
Ключевые слова: логистика, задача развозки, метод Кларка-Райта, маршрут, грузоподъёмность, транспорт, оптимизация.
Актуальность проблемы выражена в динамичном развитии розничной торговли, связанная с постоянно изменяющимися факторами внешней среды и обострением конкуренции. Товародвижение является достаточно сложной системой, динамически изменяющейся под влиянием внутренних и внешних факторов, имеющих диверсификационные взаимодействия. Таким образом, оптимизации и рационализации товародвижения не всегда достигают наивысших результатов, из-за сложности получения или переработки информации, способности к принятию решений. Преобразования логистических систем товародвижения розничных торговых предприятий в последние годы в значительной степени связаны с трансформацией отношений в контексте элементов логистической системы.
Имеется склад и список торговых точек. На базе склада находится некоторое количество единиц транспорта, которое обслуживает построенные маршруты. Грузоподъемность каждого вида транспортного средства и их количества известна. Каждая из торговых точек имеет свои запросы на товар. Запрос представлен в виде количества товара и желаемой даты получения. Известны все расстояния от склада до торговых точек и между ними. Необходимо распределить груз между транспортными средствами и найти маршруты поставки с целью минимизации общего суммарного расстояния. Следует учесть возможность наличия требования по времени доставки товара, что особенно актуально при доставке продуктов питания.
Перед началом алгоритма нужно рассчитать предел количества маршрутов использующих транспорт с не минимальной грузоподъемностью.
 |
(1) |
где qi – количество требуемого товара на точку i;
ci – грузоподъемность транспорта вида i;
ki – количество транспорта вида i;
kif– предел транспорта вида i в схеме.
Метод Кларка-Райта заключается в получении оптимальной схемы развозки, за счет нахождения маршрута, дающего наибольшее сокращение расстояния путем создания кольцевого маршрута. Для этого вводится понятие – километральный выигрыш.
На рисунке 1 показаны две схемы доставки.

На схеме доставке A отображается доставка грузов по радиальным маршрутам в пункты 1 и 2, а на схеме B – по кольцевому маршруту в те же пункты. Схема B дает результат лучше, если точки не располагаются в противоположных концах.
Километральным выигрышем называют величину, показывающую на сколько меньшее расстояние нужно будет преодолеть, строя маршрут по схеме B по сравнению с маршрутом, построенным по схеме A. Таким образом, его можно рассчитать по формуле:
|
(2) |
В общем случае мы имеем такую формулу:
Sij = li0 + l0j − lij |
(3) |
где Sij – километральный выигрыш;
li0, l0j – расстояние между пунктами i и j и складом соответственно;
lij – расстояние между пунктами i и j.
По заданной формуле строится матрица километральных выигрышей.
Описание алгоритма
Шаг 1 – находим ячейку с максимальным значением на матрице километральных выигрышей:
Smax = max (Sij) |
(4) |
Обозначим координаты точки в матрице, как i*и j*
При поиске максимального элемента нужно учесть ряд условий:
а) точки i*и j*не входят в состав одного и того же маршрута;
б) точка i*или j*является начальным или конечным пунктом, того маршрута, в который он войдет, а другая точка не используется в других маршрутах;
в) точки i*и j* является начальным и конечным пунктом, тех маршрутов, которые они объединяют;
г) ячейка с координатами (i*, j*) или (j*, i*) не использовались ранее.
Если удалось найти такую ячейку, которая удовлетворяет четырем указанным условиям, то переход к следующему шагу. Если нет, то к шагу 4.
Если точки i*и j* не использовались в других маршрутах, то создать новый.
Шаг 2 – проверить выполнения условия грузоподъемности на протяжении всего маршрута и выбрать транспорт, подходящий для маршрута:
| Qi + q ≤ cn | (5) | ||
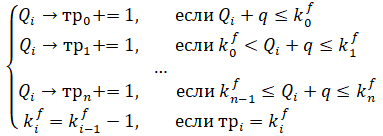 |
(6) |
где Qi – общее количества груза требуемого маршрутом;
q – количество требуемого товара на добавляемую точку;
cn – максимальная грузоподъемность.
При необходимости добавления временного лимита T для специфического груза, необходимо проверить, не превышает ли время, необходимое на маршрут, заданное ограничение:
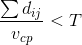 |
(7) |
где
– протяженность маршрута до точки в километрах;
vср – средняя скорость выбранного транспорта по городу.
Если условие выполняется, то переход к шагу 3, если нет – к шагу 1.
Шаг 3 – добавляем полученную точку в начало/конец маршрута и возвращаемся к шагу 1.
При добавлении нового маршрута, транспорт добавляется в очередь с приоритетом, где первому в очереди необходимо минимальное количество времени для обслуживания выделенного ему маршрута.
Если лимит использования транспорта достигает максимума, то для обслуживания следующего маршрута берется первый транспорт из очереди. При этом вся очередь пересчитывается с вычетом первого, который добавляется в очередь со временем, необходимым для обслуживания нового маршрута.
Шаг 4 – рассчитываем суммарное расстояние, которое необходимо пройти для покрытия всех маршрутов.
Используя данный алгоритм в реальной системе можно добиться уменьшения количества буферных складов и значительно уменьшить расходы на логистику. Алгоритм проверен на тестовых примерах, показывающих, что с данными изменениями вычислительная сложность алгоритма не увеличивается.
Гери, М. Вычислительные машины и труднорешаемые задачи / М. Гери, Д. Джонсон. – Москва: Мир, 1982 – 416 с.
Логистика [Электронный ресурс] // Википедия – Режим доступа: https://ru.wikiversity.org/wiki/Логистика – Загл. с экрана.
Навигационная система [Электронный ресурс] // Википедия – Режим доступа: https://ru.wikipedia.org/wiki/Навигационная_система– Загл. с экрана.
Метод Кларка-Райта. Оптимальное планирование маршрутов грузоперевозок [Электронный ресурс] // Инфостар – Режим доступа: https://infostart.ru/public/443585/– Загл. с экрана.