Hindawi Publishing Corporation
ISRN Обработка сигналов
Том 2013, ID статьи 156540, 5 страниц
http://dx.doi.org/10.1155/2013/156540
Исследовательская статья
Прогнозирование погоды с использованием алгоритма скользящего окна
Piyush Kapoor1 and Sarabjeet Singh Bedi2
1 Kvantum Inc., Gurgaon 122001, India
2 MJP Rohilkhand University, Bareilly 243006, India
Корреспонденцию следует направлять в Piyush Kapoor; piyushkapoor7@yahoo.com
Получено 7 июня 2013 года; принято 19 августа 2013 года
Академические редакторы: W.-L. Hwang and G. A. Tsihrintzis
Авторское право © 2013 P. Kapoor and S. S. Bedi. Это статья открытого доступа, распространяемая в соответствии с указаниями Creative Commons. Лицензия разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии, что оригинальная работа должным образом цитируется.
Чтобы предсказать будущие погодные условия, необходимо использовать изменение условий в прошлые годы. Вероятность того, что погодные условия рассматриваемого дня будут совпадать с тем же днем предыдущего года, очень мала. Но вероятность того, что будет совпадение в пределах соседних двух недель предыдущего года, очень велика. Таким образом, для двухнедельного периода, рассмотренного в предыдущем году, выбирается скользящее окно, равное размеру недели. Затем каждую неделю скользящего окна сопоставляют с неделей текущего года. Окно, которое лучше всего подбирается, предназначено для участия в процессе прогнозирования погодных условий. Прогноз сделан на основе алгоритма скользящего окна. Ежемесячные результаты рассчитываются за три года для проверки точности. Результаты этого подхода показали, что метод, используемый для прогнозирования погодных условий, является достаточно эффективным со средней точностью 92,2%.
1. Введение
Прогнозирование погоды в основном связано с прогнозированием погодных условий в заданное время в будущем. Прогнозы погоды предоставляют важную информацию о погоде в будущем. Существуют различные подходы к прогнозированию погоды — от относительно простых наблюдений за небом до весьма сложных компьютеризированных математических моделей. Прогнозирование погодных условий имеет большое значение для различных применений. Некоторые из них — мониторинг климата, выявление засухи, прогнозирование суровых погодных условий, сельское хозяйство и производство, планирование в энергетике, авиационной промышленности, связи, распространение загрязнения и т.д. [1]. В ходе военных операций имеется значительный исторический опыт, свидетельствующий о том, что погодные условия изменили ход боевых действий. Точный прогноз погодных условий является сложной задачей в связи с динамической природой атмосферы, погодные условия в любом случае могут быть представлены некоторыми переменными величинами. Из этих переменных величин выбираются наиболее значимые для участия в процессе прогнозирования. Выбор переменных зависит от места, для которого будет сделан прогноз. Переменные и их диапазон всегда меняются от места к месту. Погодные условия любого дня имеют некоторую связь с погодными условиями, существовавшими в тот же период предыдущего года и на предыдущей неделе.
Разработана статистическая модель [2], которая может прогнозировать количество осадков и температуру с помощью прошлых данных, используя нейронную сеть с временной задержкой и прямой связью. Искусственная нейронная сеть была объединена с генетическим алгоритмом, чтобы получить более оптимизированный прогноз [3]. Улучшенная методика, в которой используется искусственная нейронная сеть с фотоэлектрической системой, была предложена ISA и другими. [4], в которой используется модель персептрона с алгоритмом Левенберга Марквардта. Помимо нейронной сети, нечеткая логика также используется в моделях прогнозирования погоды. Количество осадков было разделено на три нечетких набора, которые можно предсказать, используя простые нечеткие правила [5]. Кроме того, Лу Фенг и Сюй Сяо Гуан [6] предложили нечеткую модель саморегрессии, которая использует форму собственного порядкового номера в соответствии с наблюдаемым числом. Коэффициенты, связанные с самим собой, были рассчитаны с использованием нечеткой логики [7]. Для системы прогнозирования погоды предлагается комбинированный подход нейронной сети с нечеткой логикой. В работе применен метод анализа основных компонентов для нечетких данных с использованием автоассоциативных нейронных сетей.
Основной недостаток в методах, предложенных выше, заключается в том, что они использовали предыдущие погодные условия, чтобы предсказать их в будущем, но основополагающая связь, которая существует между предыдущими данными, не была математически описана и проанализирована. Методы, использующие искусственные нейронные сети (ИНС), были связаны только с корректировкой весов, чтобы получить правильный результат от заданного ввода. Но никакие отношения между данными не были определены математически. Также методы ИНС страдали от таких аномалий, как локальные минимумы, переоснащение и так далее. Другая проблема заключается в том, что трудно определить, какой объем обучающих данных достаточен для корректировки весов, чтобы можно было достичь оптимальной точности прогнозируемых погодных условий. Ряд других методов прогнозирования погоды, использующих регрессию с алгоритмами машинного обучения, был предложен в источниках [8, 9]. Но математическая модель, которая могла бы представлять связь между предыдущими данными, которые могли бы использоваться для прогнозирования, все еще желательна. В этой работе предлагается новый подход к скользящему окну для прогнозирования погоды.
2. Предлагаемая работа
2.1. Методология. Погодные условия всегда немного различаются, что может зависеть от последних семи дней или около того. Здесь изменение относится к разнице между параметром предыдущего дня и параметром текущего дня. Также существует зависимость между погодными условиями, сохраняющимися в течение текущей недели, и прошлыми годами. В этой работе предлагается методология, которая могла бы математически моделировать эти два типа зависимости и использовать их для прогнозирования будущих погодных условий. Для прогнозирования погодных условий на день, эта работа будет учитывать условия, преобладающие на предыдущей неделе, то есть за последние семь дней, которые, как предполагается, известны. Также учитываются погодные условия семи предыдущих дней и семи последующих дней за предыдущий год. Например, если прогноз погоды на 16 ноября 2012 г. будет сделан, то мы примем во внимание условия с 9 ноября 2012 г. по 15 ноября 2012 г. и условия с 09 ноября по 22 ноября 2011 г. в пошлые годы. Теперь, чтобы промоделировать вышеупомянутые зависимости, изменение текущего года в течение недели сопоставляется с изменениями предыдущих лет путем использования скользящего окна. Лучше всего подобранное окно, выбрано для прогнозирования. Выбранное окно и еженедельные изменения текущего года вместе используются для прогнозирования погодных условий. Причиной применения сопоставления скользящих окон является то, что погодные условия, преобладающие в течение года, могут не совпадать или не совпадать с той же датой, какой они могли существовать в предыдущие годы. Вот почему рассматриваются семь предыдущих и семь текущих дней. Следовательно, общий период в две недели проверяется в предыдущем состоянии, чтобы найти аналогичный период в будущем. Скользящее окно — неплохая техника для захвата изменений, которые могут соответствовать изменениям текущего года.
2.2. Алгоритм скользящее окно
. В работе предлагается прогнозировать дневные погодные условия. Для этого учитывается погода предыдущих семи дней, а также двухнедельные погодные условия прошлых лет. Предположим, нам нужно спрогнозировать погоду 23 августа 2013 года, а затем мы примем во внимание погодные условия с 16 августа 2013 года по 22 августа 2013 года вместе с погодными условиями, преобладающими в период с 16 августа по 29 августа в прошлые годы. Затем вычисляется ежедневное изменение текущего года. Разница также рассчитывается на основе данных за две недели предыдущего года. В этой работе будут учитываться четыре основных параметра погоды: максимальная температура, минимальная температура, влажность и количество осадков. Следовательно, размер изменения текущего года будет представлен матрицей размером 7 × 4. И аналогично для прошлого года размер матрицы будет 14 × 4. Теперь, первый шаг - разделить матрицу размера 14 × 4 на скользящие окна. Таким образом, 8 скользящих окон могут быть выполнены размером 7 × 4 каждое. Концепция скользящего окна показана на рисунке 1.
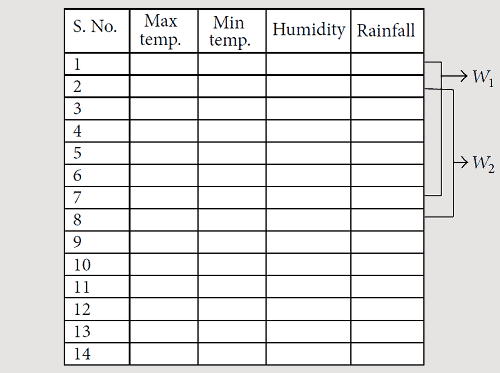
Рисунок 1: Концепция скользящего окна, где W1 представляет окно №1,
а W2 представляет окно №2.
Теперь следующим шагом является сравнение каждого окна с изменением текущего года. Для прогноза выбрано наиболее подходящее окно. Подход Евклидова расстояния используется для соответствия. Причиной взятия Евклидова расстояния является его способность представлять сходство, несмотря на свою простоту. Ниже приведены параметры, используемые для прогнозирования погодных условий:
- среднее значение: средние дневные погодные условия, то есть максимальную температуру, минимальную температуру, влажность и количество осадков. После добавляется каждое отдельно, и делится на общее количество дней
- отклонение: вычисление изменений день ото дня после определения разницы каждого параметра. Это говорит о том, как погода следующего дня связана с погодой предыдущего дня;
- Евклидово расстояние: сравнивнение изменения данных текущего и предыдущего года.
Среднее значение = Сумма парметров ÷ Колличество дней, (1)
Тем самым мы можем математически моделировать вышеупомянутые определенные зависимости. То, что соотношение между данными за предыдущий год и предыдущую неделю определяется математически, может использоваться для прогнозирования будущих условий. Скользящее окно, используемое для прогнозирования количества погодных условий n
(WC1, WC2, WC3, ... , WCn) Показано в алгоритме 1.

Алгоритм 1
Основная логика использования метода скользящего окна состоит в том, что погодные условия, преобладающие в определенный промежуток времени в году, могли не существовать в течение того же периода в предыдущем году. Например, погодные условия в первую неделю февраля 2010 года, возможно, не существовали в первую неделю февраля 2009 года. Аналогичные погодные условия могли преобладать в предыдущем году, но не обязательно на той же неделе, а через несколько дней. Вероятность нахождения подобных погодных условий максимальна при рассмотрении двухнедельного диапазона.
3. Итоги и обсуждения
Предыдущий алгоритм тестируется на основании данных о погоде за период с 2006 по 2010 годы в городе Чампават, Уттаранчал. Данные взяты из Центра прогнозирования погоды в Пантнагаре. Алгоритм был выполнен и протестирован в версии Matlab 2010a. Таким образом, при рассмотрении алгоритма данные предыдущего года используются для прогнозирования погодных условий. Следовательно, алгоритм тестируется для прогнозирования погодных условий в течение трех лет, то есть 2008–2010 гг., что проверяется по имеющимся данным. Также можно сделать вывод, что подход к обучению, используемый в алгоритме, контролируется. В тесте учитываются четыре погодных условия, то есть минимальная температура, максимальная температура, влажность и количество осадков. Температура, как правило, может быть измерена с более высокой степенью точности по сравнению с любой другой переменной погоды. Данные этих четырех факторов взяты в течение дня на протяжении ранее упомянутых четырех лет. Алгоритм также тестируется ежедневно.
На рисунках 2, 3, 4 и 5 показано изменение фактических и прогнозируемых четырех погодных условий для дня 2010 года.
Эти графики четко показывают наименьшие различия между фактическими и прогнозируемыми погодными условиями. Месячная точность прогнозируемых погодных условий приведена в таблице 1.
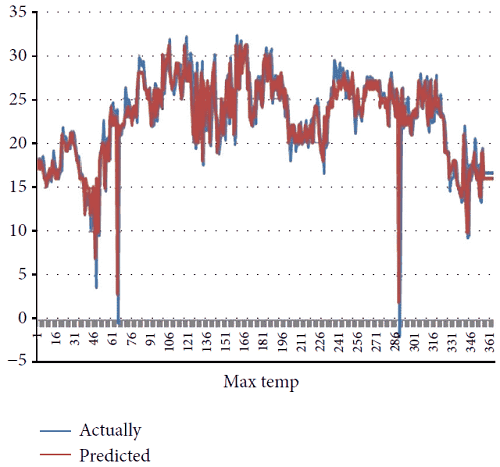
Рисунок 2: График, представляющий прогнозируемую и фактическую максимальную
температуру для 2010 года.
Таблица 1
| Месяц | Точность прогнозируемых данных |
|---|---|
| Январь | 97.24% |
| Февраль | 88.94% |
| Март | 92.25% |
| Апрель | 98.17% |
| Май | 93.49% |
| Июнь | 99.02% |
| Июль | 87.19% |
| Август | 78.83% |
| Сентябрь | 79.23% |
| Октябрь | 94.35% |
| Ноябрь | 98.78% |
| Декабрь | 95.73% |

Рисунок 3: График, представляющий прогнозируемую и фактическую минимальную
температуру для 2010 года.

Рисунок 4: График, представляющий прогнозируемую и фактическую
влажность для 2010 года.
Вышеуказанный результат погодных условий был из индийского города. В Индии типично тропический тип погоды, то есть погода, которая имеет все разновидности. Город Чампават находится в штате Уттаранчал, который лежит в плоскостях Ганга. Ежемесячная точность в Таблице 1 может быть понята из следующих фактов. Апрель, май и июнь считаются летом с высокой температурой. Ноябрь, декабрь и январь — это зимы с низкими или холодными температурными условиями. Таким образом, такие факторы, как температура, довольно постоянны в эти месяцы, и, следовательно, точность для них также высока. Напротив, месяцы, такие как февраль, март, август и сентябрь, считаются месяцами, когда погода меняется, то есть фаза перехода от одного сезона к другому. В феврале и марте зимний сезон сменяется на летний. А в августе и сентябре лето кончается, и начинается зима.
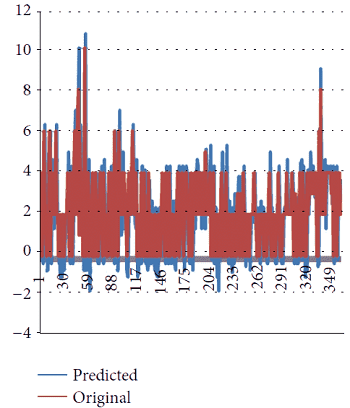
Рисунок 5: График, представляющий прогнозируемый и фактический
дождь в 2010 году.
И, следовательно, погодные условия становятся крайне непредсказуемыми в эти месяцы. Также отмечается, что погодные условия сильно различаются в эти месяцы из года в год. Это также отражается на результатах.
4. Заключение и будущая работа
Было найдено, что сравнение изменений погодных условий с использованием скользящего оконного подхода является очень точным, за исключением месяцев сезонных изменений, когда условия крайне непредсказуемы. Результаты могут быть изменены путем изменения размера окна. Точность непредсказуемых месяцев может быть увеличена путем увеличения размера окна до одного месяца. Поскольку методы ИНС очень хороши для отображения входов и выходов, алгоритм скользящего окна, если он включен в ИНС, может значительно улучшить результаты даже в течение месяцев сезонных изменений.
Ссылки
- Y. Radhika and M. Shashi,
Atmospheric temperature prediction using support vector machines,
International Journal of Computer Theory and Engineering, vol. 1, no. 1, pp. 1793–8201, 2009. - L. L. Lai, H. Braun, Q. P. Zhang et al.,
Intelligent weather forecast,
in Proceedings of the International Conference on Machine Learning and Cybernetics, pp. 4216–4221, Shanghai, China, August 2004. - J. Gill, B. Singh, and S. Singh,
Training back propagation neural networks with genetic algorithm for weather forecasting,
in Proceedings of the 8th IEEE International Symposium on Intelligent Systems and Informatics (SIISY ’10), pp. 465–469, September 2010. - I. S. Isa, S. Omar, Z. Saad, N. M. Noor, and M. K. Osman,
Weather forecasting using photovoltaic system and Neural Network,
in Proceedings of the 2nd International Conference on Computational Intelligence, Communication Systems and Networks, pp. 96–100, July 2010. - L. Zuoyong, C. Zhenpei, and L. Jitao,
A model of weather forecast by fuzzy grade statistics,
Fuzzy Sets and Systems, vol. 26, no. 3, pp. 275–281, 1988. - L. F. Lu Feng and X. X. G. Xu xiaoGuang,
Aforecastingmodel of fuzzy self-regression,
Fuzzy Sets and Systems, vol. 58, no. 2, pp. 239–242, 1993. - T. Denoeux and M. -H. Masson,
Principal component analysis of fuzzy data using autoassociative neural networks,
IEEE Transactions on Fuzzy Systems, vol. 12, no. 3, pp. 336–349, 2004. - R. Collobert and S. Bengio,
SVMTorch: support vector machines for large-scale regression problems,
Journal of Machine Learning Research, vol. 1, no. 2, pp. 143–160, 2001. - P. -S. Yu, S. -T. Chen, and I. -F. Chang,
Support vector regression for real-time flood stage forecasting,
Journal of Hydrology, vol. 328, no. 3–4, pp. 704–716, 2006.