УДК 004.942

РЕАЛИЗАЦИЯ АЛГОРИТМА ПОИСКА ПУТИ ДЛЯ ТРАНСПОРТНОГО СРЕДСТВА

Аннотация

В данной работе выполнен анализ существующих алгоритмов поиска рационального пути. Рассмотрены проблемы, связанные с автоматизацией движения транспортных средств. Выявлены основные сложности построения реалистичных маршрутов с помощью эвристических методов, определены способы улучшения результатов. Выполнен анализ математической модели алгоритма А* и разработана программа моделирования на языке высокого уровня. Намечены направления дальнейших исследований.

Ключевые слова: алгоритм, транспортное средство, траектория движения, А*.

IMPLEMENTATION OF A PATH SEARCH ALGORITHM FOR A VEHICLE

Kravchenko Mikhail, Kryvosheyev Sergey, Malcheva Raisa
Donetsk national technical university, Donetsk, Donetsk People's Republic

Abstract

In this paper the existing algorithms for searching of the rational path are analyzed. The problems associated with the rational automatic movement of vehicles are considered. The main difficulties in realistic routes creation with the help of heuristic methods are revealed. The ways of the results improving are determined. The mathematical model of the algorithm A * is analyzed and a simulation program is developed in a high-level language. Directions for further research are outlined.

Keywords: algorithm, vehicle, direction analysis, trajectory, А*.

Введение

В настоящее время количество транспортных средств непрерывно растет. Актуальными становятся проблемы, связанные с составлением маршрутов и анализом трафика. Рационально спланированный маршрут и автоматизация управления позволят сэкономить затраты топлива и, соответственно, уменьшить вред экологии, а также свести к минимуму аварии и катастрофы [1]. Все больше различных исследовательских центров по всему миру развивают это направление.

Задача поиска пути сводится к анализу препятствий, которые могут встретиться на траектории движения, и их рациональному обходу.

Для данной задачи разработано множество алгоритмов, которые активно используются в прокладке сетей, разводке печатных плат, движения объектов в компьютерных играх. Создание симуляторов, позволяющих моделировать поведение транспортного средства в условиях изменяющейся обстановки снижает потребность в дорогостоящих экспериментах [1, 2].

Большой проблемой остается быстродействие, с которым будут выполняться расчеты движения и анализ выбора маршрута, что накладывает определенны ограничение на выбор оптимального алгоритма поиска пути. Актуальной остается задача реализации поиска пути с использованием минимально возможного количества памяти и времени расчета.

Постановка задачи

Анализ направления движения транспортного средства (ТС) подразумевает наличие данных об его местонахождении и окружающей обстановке. ТС имеет четко фиксированный набор вариантов продолжения движения: продолжить движение, уменьшить скорость, увеличить скорость, задний ход, повернуть вправо/влево.

Проведенный анализ существующих алгоритмов показал, что не все из них подходят для данного типа задач. Системы, работающие в режиме реального времени, ограничены по скорости на ответ допустимым порогом 100 мс [3]. Необходимо так же учитывать тот факт, что ТС не может мгновенно изменить курс. Скорость «реакции» на изменение положения рулевого механизма зависит от массы ТС, его сцепления с поверхностью и других факторов.

Исходя из вышеперечисленного, задачу поиска пути можно условно разделить на 2 этапа:

– построение оптимального маршрута по алгоритму, удовлетворяющему необходимые ограничения на

использование ресурсов и времени;

– постобработка результатов первого этапа для получения реалистичных показателей.

В зависимости от выбора алгоритма эти два этапа могут быть объединены в один, если предусмотрена оптимизация данных во время поиска пути. Второй этап необходим, поскольку ТС не может мгновенно изменить траекторию движения. И, следовательно, крутых поворотов в предоставленном маршруте первым этапом необходимо избежать.

Описание алгоритма поиска пути

Алгоритм А* является одним из лучших алгоритмов поиска пути. Он находит маршрут от стартовой вершины к финальной с наименьшей стоимостью [4]. Был разработан в 1968 году Питером Хартом, Нильсом Нильсоном и Бертрамом Рафаэлем. Данный алгоритм, по сути, является расширением алгоритма Дейкстры, но достигает более высокой производительности за счет введения в работу алгоритма эвристической функции [5]. Типичная формула эвристики выражается в виде:

f(n) = g(n) + h(n), (1)

где f(n) — значение оценки, назначенной узлу n;

g(n) — наименьшая стоимость прибытия в узел n из точки старта;

h(n) — эвристическое приближение стоимости пути к цели от узла n

Т.о. алгоритм в себе учет длины пути и эвристическую оценку стоимости перехода [6]. Суть алгоритма заключается в том, что на каждом шаге происходит анализ всех соседних ячеек. В случае разбиения исходного поля на сетку ячеек получается не более 8 потомков и для каждого вычисляется стоимость перехода по формуле (1). Пример приведен на рис.1.

Как видно из примера, в закрытый список попадет ячейка со стоимостью 40, хотя для оптимального маршрута логично было бы взять одну из ячеек со стоимостью 54. Этот недостаток будет исправлен на следующем шаге, когда произойдет пересчет стоимости перехода.

На рис.2 показан полный маршрут ячеек, попавших в «закрытый список» (выделенные ячейки) и «открытый список» (не выделенные ячейки со стрелочками).

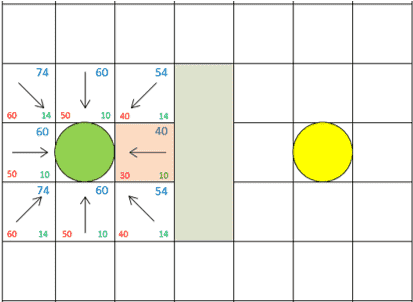
Рисунок 1 — Пример заполнения открытого списка на первом шаге

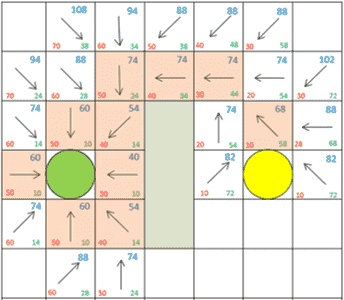
Рисунок 2 — Пример нахождения маршрута по алгоритму А*

Анализ известных модификаций алгоритма

В случаях прокладки маршрута для реальных систем данный алгоритм имеет ряд недостатков.

Во-первых, в случае, когда поле будет достаточно большим и занимать тысячи ячеек может возникнуть проблема с количеством используемой памяти списками.

Во-вторых, время на поиск пути может превзойти предельно допустимое время ответа.

В-третьих, алгоритм находит не самый короткий путь.

Для устранения данных недостатков разработаны следующие модификации.

Beam search (поиск по лучу).

В классическом А* в открытый список сохраняются все вершины, которые могут потребоваться для выполнения поиска. Данная модификация предусматривает наложение ограничений на размер этого списка. То есть после того, как открытый список полностью заполняется для добавления в него очередных ячеек, сначала удаляются те, вероятность использования которых меньше всего. Применяя данную модификацию можно избежать проблемы с количеством используемой памяти.

Iterative deepening (итеративное погружение).

Идея этого метода заключается в том, чтобы проверить следующие несколько шагов алгоритма и в случае, если не наблюдается улучшение результата – прекратить поиск в данном направлении. Продолжение поиска, пока не было улучшения производится на величину f, которое и задает величину погружения. Таким образом при первом проходе будет проведено малое количество узлов, а при последующих проходах их количество будет увеличиваться. Следовательно, в случае, когда нет препятствий или их обход не превзойдет величину погружения f количество задействованных ячеек в анализе будет меньше, чем в обычном алгоритме А*. Эта модификация в определенных случаях даст значительный выигрыш по времени и количеству используемой памяти.

Dynamic weighting (использование переменных весов).

Данная модификация предполагает, что в начале поиска требуется как можно быстрее достичь области, содержащей финальную ячейку пути. В конце поиска более важно дости- жение конкретной ячейки. Предлагается следующая модификация функции веса:

f(n) = g(n) + w(n) × h(n), (2)

где w(n) – весовой коэффициент, назначенный узлу n.

При приближении к финальной ячейке вес уменьшается. Это снижает значимость эвристики и увеличивает относительную важность фактической стоимости пути.

Bidirectional search (двунаправленный поиск).

Исходя из названия понятно, что поиск будет происходить одновременно из двух ячеек на встречу друг к другу. Это позволит вместо одного большого списка использовать два поменьше. Главным недостатком данной модификации является то, что не во всех случаях место встречи поиска будет оптимальным.

Theta*.

Основной проблемой поиска пути является отдаленность выбранного маршрута от оптимального обхода препятствий. Отличием данной модификации является то, что Theta* позволяет в качестве «родителя» для каждой ячейки выбрать любую, в отличии от А*, где «родителем» может быть только соседняя ячейка. Применение данной модификации позволит получить более реалистичные показатели поиска пути, но требует больше времени и дополнительных расходов памяти [4].

Разработка стратегии поиска рационального пути

В качестве получения оптимальных результатов поиска пути можно использовать следующую комбинацию алгоритмов:

шаг 1: при помощи алгоритма А* найти маршрут;

шаг 2: удалить точки, лежащие на одной прямой;

шаг 3: для каждой пары точек из небольшого количества применить алгоритм проверки наличия пути по прямой и в случае возможности изменить маршрут.

На настоящий момент выполнены реализация и тестирование первого этапа с использованием языка программирования С++.

Разработка программы моделирования алгоритма

В качестве используемого языка программирования был выбран язык С++. Это обусловлено планируемой реализацией алгоритма как части общей системы моделирования движения транспортного средства с использованием параллельных архитектур вычислительных систем, таких, как технология CUDA, для ускорения выполнения поиска оптимального пути. На рис.3. показаны результаты моделирования при использовании классического алгоритма и А*.

Рисунок 2 — Пример поиска пути:
а) классическим алгоритмом А*;
б) оптимальный маршрут

В качестве доработки введено ограничение на срез углов вблизи препятствия. Данное ограничение реализовано функцией, возвращающей булевое значение, листинг которой представлен ниже.

Листинг 1

prebool  SrezUglov(Node  **Matr,  Point  Start,  Point  End)
{
  if  (Start.x  !=  End.x  &&  Start.y  !=  End.y)  //  переход  по  диагонали
  {
    if(Matr[Start.x][End.y].Znach  ==  1  ||  Matr[End.x][Start.y].Znach==  1) 
      return  true;
  }
return  false;
}

В случае, когда переход происходит по диагонали и соседней ячейкой является препятствие, необходимо запретить возможность такого перехода.

Проведенное тестирование показало явные ошибки в нахождении пути и подтвердило необходимость применение модификаций.

Выводы

Выполненный анализ показал, что не существует универсального алгоритма поиска пути. Для каждой отдельной задачи необходимо применять модификации к алгоритму. В ходе моделирования были выявлены недостатки алгоритма А* и намечены способы их устранения. В дальнейшем планируется адаптировать рассмотренный алгоритм к реализации с применением технологий параллельных вычислений.

Литература

1. Кривошеев С.В. Исследование эффективности параллельных архитектур вычислительных систем для расчета параметров движения транспортного средства // Научные труды Донецкого национального технического университета. Выпуск № 1(10)-2(11). Серия «Проблемы моделирования и автоматизации проектирования». — Донецк, ДонНТУ, 2012. С. 207–214.

2. Мальчева Р.В., Кривошеев С.В., Завадская Т.В. Разработка симуляторов транспортных средств с использованием операционной системы Android // Информатика и кибернетика. 2015. № 2. С. 76–81.

3. Eric Hansen, Terry Huntsberger and Les Elkins. Autonomous maritime navigation: developing autonomy skill sets for USVs // Proc. SPIE 6230, 62300U (2006).

4. Басараб М.А., Домрачева А.Б., Купляков В.М. Алгоритмы решения задачи быстро-го поиска пути на географических картах // Инженерный журнал: наука и инновации, 2013. № 11. — URL: http://engjournal.ru/ catalog/it/hidden/1054.html

5. Изотова Т.Ю. Обзор алгоритмов поиска кратчайшего пути в графе // Новые информационные технологии в автоматизированных системах, 2016. С. 341–344.

6. Bryan Stout. The Basics of A* for Path Planning. In Game Programming Gems. // Charles River Media, 2000. PP. 254–263.