УДК 630 *0.383
ОБОСНОВАНИЕ ВЫБОРА АЛГОРИТМА ПОИСКА КРАТЧАЙШЕГО ПУТИ ДЛЯ ПОСТРОЕНИЯ СХЕМЫ СЕТИ ЛЕСОВОЗНЫХ ДОРОГ
Р.А. Черных
ГОУ ВПО «Сибирский государственный технологический университет»
660049 Красноярск, ул. Мира 82, e-mail: hydra1isk@ya.ru
Приводится анализ существующих алгоритмов поиска кратчайших путей в графах. Рассмотрены методики определения и освоения экономически доступных лесных ресурсов. Проанализирован алгоритм проектирования схем сети лесных дорог на основе алгоритма Флойда-Уоршелла. Предлагается в этот алгоритм внести дополнительные вершины, позволяющие учесть особенности компонентов местности (рельеф, реки, болота и т.п.) и оптимизировать расположение разветвлений дорог. Кроме того, предлагается выполнять поиск кратчайших путей с помощью алгоритма Дейкстры.
Ключевые слова: аалгоритм поиска кратчайших путей, сеть лесных дорог, алгоритм Флойда-Уоршелла, алгоритм Дейкстры
The analysis of existing algorithms of search of the shortest ways in columns is resulted. Techniques of definition and de- velopment of economically accessible forest resources are considered. The algorithm of designing of schemes of a net of forest roads on the basis of Floyd-Uorshell's algorithm is analyzed. It is offered to bring the additional tops in this algorithm, allowing to consider features of ingredients of district (a land forms, the rivers, bogs, etc.) and to optimize an arrangement of branching of roads. Besides it is offered to carry out search of the shortest ways by means of Dijkstra's algorithm.
Key words: algorithms of search of the shortest ways, net of forest roads, Floyd-Uorshell's algorithm, Dijkstra's algorithm
ВВЕДЕНИЕ
Одним из важнейших условий, способствующим высокой эффективности работы автомобильного транспорта, является наличие благоустроенных дорог на территории предприятий лесной промышленности. Эффективное использование лесных ресурсов невозможно осуществить без решения задачи оптимизации дорожно-транспортной схемы, с учетом очередности введения в эксплуатацию отдельных ее участков. На данный момент в России на одну тысячу гектаров леса приходится всего лишь 0,35 километра лесовозных дорог, что является недостаточным и снижает эффективность работы лесного комплекса. Это в 10–15 раз меньше чем в Германии, Швеции или Канаде. С целью исправления данной ситуации в краевой администрации была разработана программа развития лесного комплекса на ближайшие 10 лет, принятая в 2007 году. Одним из основных разделов программы является развитие транспортной инфраструктуры. Одним из главных факторов оптимизации транспортной схемы и оценки экономической доступности ресурсов лесосырьевой базы является оптимизация схемы сети лесных дорог, связывающей отдельные лесоучастки с нижним складом сырья, с учетом существующих транспортных путей, основных природно-климатических и технико-экономических факторов. Различные авторы предлагают разные способы определения экономически доступных лесных ресурсов и рассматривают разные способы построения схемы лесных дорог. В работе (Андреева, 2007) разработан методический подход для определения экономической доступности лесных ресурсов. Авторы определяют экономическую доступность без проектирования схемы сети дорог, определяя затраты по существующим нормативам, и учитывают только приближенное расстояние вывозки. В результате подобного подхода экономическая доступность определяется приближенно. В своей работе (Чижов, 2001) тоже не проектирует схему лесных дорог, а ограничивается определением зон экономической доступности. Сам автор отмечает, что такой метод является приближенным, но простым. В работе (Гуров, 1996) авторами предлагается методика планирования транспортной системы лесного предприятия по критерию максимума эколого-экономического эффекта, но в опубликованных в печати данных не приводится непосредственно метод оптимизации сети лесных дорог. Эта задача может быть решена с помощью графоаналитической модели, основанной на теории графов. Более того, в большинстве работ, где решается эта задача, применяется графо – аналитический метод. По этому методу каждый отдельный лесоучасток представляется в виде одной из вершин графа, а все возможные дороги, соединяющие лесоучастки – ребра графа (Болотов, 2005; Мохирев, 2007). В работах, где проекти-руется транспортная схема участка лесного фонда, экономическая доступность определяется наиболее точно по сравнению с остальными методиками.
Особенности данной задачи:
– для построения сети дорог используем полный неориентированный граф;
– в графе большое количество вершин;
– в графе нет ребер с отрицательным весом;
– изначально нет сети дорог, либо существует ее незначительная часть;
– все вершины, включенные в схему, должны быть соединены с первой вершиной путями минимальной
«длины»;
– в конечной схеме дорог не может быть циклов;
– каждое вновь добавленное ребро влияет на мат-рицу весов графа;
– после добавления очередного ребра в схему, необходимо пересчитывать матрицу весов графа;
– в конечную схему дорог могут быть включены не все вершины графа;
– при построении сети дорог необходимо знать, не только «длину» кратчайшего пути до вершины, но
список вершин, через которые он проходит;
– на вес ребра влияют два несвязанных параметра: затраты на строительство дороги и затраты на вывозку
всего сырья с выдела.
Основной частью любого алгоритма, позволяющего построить схему сети дорог, является процесс поиска кратчайшего пути между нижним складом и центрами выделов. Следует уделить особое внимание выбору этого алгоритма, так как именно он выполняет основную часть работы программы и во многом определяет эффективность и время работы программы. Исходя из особенностей задачи, следует, что алгоритм поиска кратчайшего пути должен обладать определенными свойствами. К ним следует отнести эффективную работу с полными графами, малую сложность алгоритма (это одна из важнейших характеристик подобных алгоритмов). Кроме того, алгоритм должен искать пути между одной вершиной графа и всеми остальными и в нем должна быть возможность сохранения информации о маршруте между вершинами. Для нахождения кратчайших путей в графах разработано и реализовано на различных языках программирования много различных алгоритмов. К ним можно отнести алгоритмы: Дейкстры, Дейкстры–Грибова, Левита, Йена, Флойда–Уоршелла, Форда–Беллмана, Джонсона. Рассмотрим коротко все эти алгоритмы. Алгоритм Дейкстры – алгоритм на графах, изобретенный Э. Дейкстрой. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. В процессе работы алгоритма поддерживаются три множества:
– М0 – вершины, расстояние до которых уже вычислено (но, возможно, не окончательно);
– М1 – вершины, расстояние до которых вычисляется;
– М2 – вершины, расстояние до которых еще не вычислялось.
В простейшем случае, сложность алгоритма составляет O(n2 + m). Здесь n – количество вершин графа, m – количество ребер графа. Эффективность метода Дейкстры существенно зависит от того, как организован поиск во множестве М1 вершины с наименьшим текущим расстоянием. Модификация Грибова заключается в том, что вершины разбиваются на подмножества с близкими, отличающимися меньше чем на минимальную длину дуги, значениями кратчайшего пути в текущую вершину на данном шаге (такие подмножества называются ведрами). Затем на каждой итерации берется непустое ведро, соответствующее минимальному значению расстояния. Алгоритм Левита позволяет найти кратчайшие пути от заданной вершины до всех остальных вершин. Алгоритм Левита напоминает метод Дейкстры – в процессе работы поддерживаются три множества (M0, M1, M2) Вершины, входящие в множество М1, делятся на два упорядоченных множества – основную и приоритетную очередь. Каждой вершине сопоставляется неотрицательное значение длины кратчайшего из известных на данный момент путей в нее из начальной вершины. В сравнении с методом Дейкстры метод Левита проигрывает на том, что некоторые вершины приходится обрабатывать повторно, а выигрывает на более простых алгоритмах включения и исключения вершин из множества M1. Эксперименты показывают, что для графов с «геометрическим» происхождением, т.е. для графов, построенных на основе транспортных сетей и реальных расстояний, метод Левита оказывается наиболее быстрым. Он выигрывает и по размеру программы. Метод Левита обладает еще и тем преимуществом перед методом Дейкстры, что он применим в случае отрицательных длин дуг. Сложность алгоритма составляет O(n*m) (Романовский, 2003; Левитин, 2007). Алгоритм Йена предназначен для нахождения нескольких путей минимальной суммарной длины во взвешенном графе с неотрицательными весами между двумя вершинами. Алгоритм Беллмана–Форда решает задачу о нахождении кратчайших путей из одной вершины во все остальные для случая, когда веса ребер могут быть отрицательными. Кроме того алгоритм контролирует отсутствие циклов отрицательного веса, достижимых из исходной вершины. Если в графе нет циклов отрицательного веса, алгоритм находит кратчайшие пути из заданной вершины во все остальные, если же в графе есть циклы отрицательного веса, то, по крайней мере, для некоторых вершин кратчайшего пути не существует. Идея алгоритма, также как и алгоритма Дейкстры, основана на последовательной релаксации ребер, пока не будут найдены кратчайшие расстояния. Время работы алгоритма Форда–Беллмана есть O(n*m), стоимость инициализации есть O(n), а стоимость проверки на цикл отрицательного веса – O(m).
Алгоритм Джонсона позволяет найти кратчайшие пути между любыми двумя вершинами графа за O(n2log(n)+n*m). Следовательно, для достаточно разреженных графов, он эффективнее альтернативных алгоритмов возведения в квадрат матрицы весов и алгоритма Флойда–Уоршелла.
Этот алгоритм основан на идее изменения весов ребер графа. Если для ребер найти такую функцию, которая изменяет их веса, обеспечивая их неотрицательность и оставляя кратчайшие пути такими же (то есть состоящими из тех же ребер).
Алгоритм Флойда–Уоршелла это динамический алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенного ориентированного графа. Его очень легко реализовать на любом языке программирования. Сложность алгоритма O(n3), т.е. алгоритм имеет кубическую сложность. Тем не менее, алгоритм определяет только кратчайшие расстояния между всеми парами вершин, но не сохраняет информации о кратчайших путях (Левитин, 2007). Из рассмотренных выше алгоритмов можно сразу исключить алгоритм Йена, так как он предназначен для поиска путей равных по длине кратчайшему. В данной задаче до точки может быть только один путь. Алгоритм Джонсона эффективен только для разреженных графов, а при построении сети дорог используется полный граф. Остальные алгоритмы рассмотрены в книге И.В. Романовского. В ходе рассмотрения этих методов автором были сделаны такие выводы:
– «...Эффективность метода Дейкстры существенно зависит от того, как организован поиск вершины с наименьшим текущим расстоянием...»
– «...Несмотря на очень высокую эффективность метода Дейкстры–Грибова, в практических задачах с «географической» системой расстояний еще более эффективен метод, принадлежащий Б. Ю. Левиту... В сравнении с методом Дейкстры метод Левита проигрывает на том, что некоторые вершины приходится обрабатывать повторно, а выигрывает на более простых алгоритмах включения и исключения вершин из множества М3. Эксперименты показывают, что для графов с –геометрическим» происхождением, т.е. для графов, построенных на основе транспортных сетей и реальных расстояний, метод Левита оказыва-ется наиболее быстрым». В данной задаче ребра имеют значительный вес и несильно различаются между собой по величине и разбиение вершин на группы по принципу Дейкстры–Грибова может оказаться неэффективным, так как в одну группу может попасть одновременно много вершин или даже все. Что же касается алгоритма Левита, то он не имеет ни каких преимуществ в данном случае с алгоритмом Дейкстры, так как исходный граф строится не на основе транспортной сети, дуг с отрицательным весом нет, вес ребер графа определяется не только на основе расстояний между вершинами. В итоге из всех перечисленных алгоритмов лучше всего использовать алгоритм Дейкстры. Для решения данной задачи в рабо-тах (Болотов, 2005; Мохирев, 2007) был предложен алгоритм на основе алгоритма Флойда–Уоршелла, блок–схема которого изображена на рисунке 1. Этот алгоритм обладает рядом недостатков: во-первых, в качестве вершин графа использовались только центры выделов, что снижает точность расчета, во-вторых, использование в качестве алгоритма поиска кратчайших путей алгоритм Флойда–Уоршелла приводит к увеличению сложности алгоритма. Также при выполнении алгоритма не учитывались особенности рельефа местности, эти данные необходимо было корректировать вручную, после выполнения алгоритма. С целью исправления этих недостатков нами был разработан алгоритм, представленына рисунке 2.
Расшифровка блоков алгоритма, представленного на рисунке 1.
1. Присвоение каждому элементу промежуточной матрицы суммы соответствующих элементов матриц стоимостей прокладки и восстановительных работ. 2. Нахождение совокупности маршрутов, составляющих минимальное покрывающее дерево исходного графа. 3. Вычисление суммарной стоимости строительства дорог данных маршрутов с учетом стоимости работ по восстановлению. 4. Сравнение ее с суммарной стоимостью, полученной на предыдущей итерации. Если они равны – переходим к шагу 9, иначе – к шагу 5 итерационной процедуры. 5. Анализ полученного промежуточного решения для поиска повторяющихся участков, а также для определения первого и последнего года использования каждого ребра. 6. Расчет новой матрицы весов. 7. Расчет по алгоритму Флойда–Уоршелла кратчайших маршрутов. 8. Переход к шагу 3. 9. Анализ решения для поиска лесосек, разработка которых экономически неэффективна. Если таких лесосек нет – решение найдено, иначе – переходим к шагу 10. 10. Присвоение статуса "вспомогательных" вершинам, прокладка маршрутов к которым признана экономически нецелесообразной.
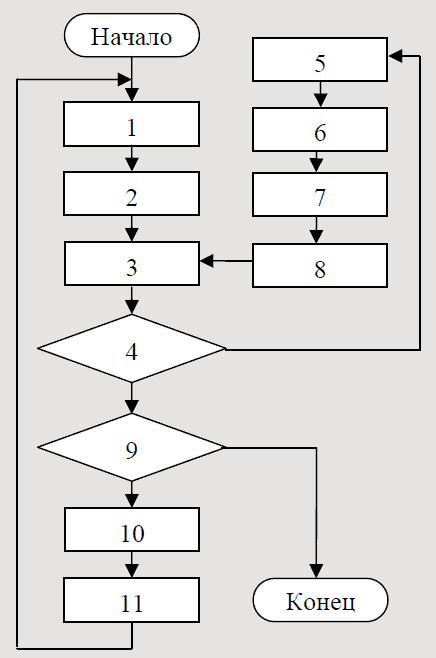
Рисунок 1 – Алгоритм построения оптимальной транспортной схемы
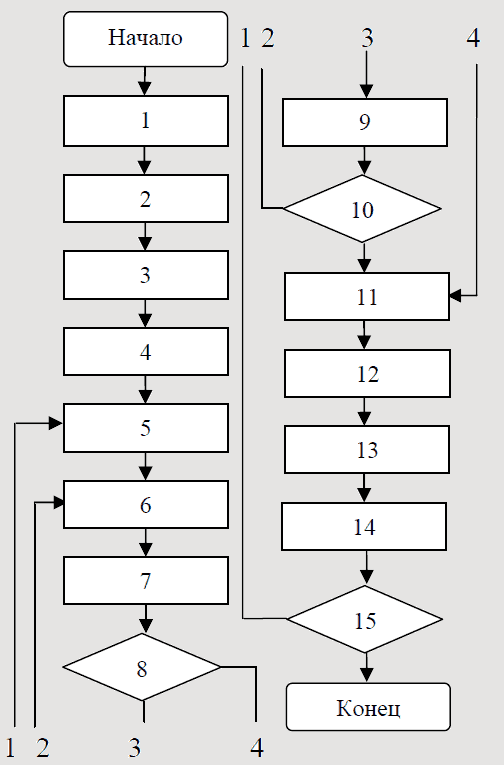
Рисунок 2 – Алгоритм построения схемы сети лесовозных дорог
Расшифровка блоков алгоритма, представлен-ного на рисунке 2.
1. Ввод матрицы стоимостей строительства. 2. Ввод матрицы стоимостей восстановления. 3. Ввод данных об уже проложенных дорогах, особенностях рельефа местности, реках, болотах и т.п. 4. Формирование первоначальной матрицы весов ребер. 5. Создание списка неосвоенных выделов, для данного этапа. 6. Построение минимального покрывающего дерева. 7. На всех ребрах графа определяются дополнительные точки, и выполняется поиск длин кратчайших путей до центров всех неосвоенных выделов и определение их рентабельности. 8. Добавление в схему транспортной сети выдела с минимальными транспортными затратами и неотрицательной рентабельностью (также вершина исключается из списка неосвоенных выделов), если таких вершин нет, то переходим к пункту 11. 9. Дорога до него отмечается, как построенная и корректируется матрица весов ребер. 10. Если есть еще неосвоенные выделы, то переход к пункту 6. 11. Определение грузопотока для всех дорог сети. 12. Выбор типа дорожного покрытия для всех дорог, построенных на текущем этапе, и определение всех данных по выделам, освоенным на текущем этапе. 13. Все нерентабельные выделы текущего этапа переносятся в список неосвоенных выделов следующего этапа. 14. Если еще не рассмотрены все этапы, то прейти к рассмотрению очередного временного этапа. 15. Сохранение всех полученных данных.
При построении схемы сети дорог, используя алгоритм, приведенный на рисунке 2, сразу учитываются особенности рельефа местности, реки и т.п. Все эти данные вносятся в расчет вместе с исходными данными и впоследствии учитываются программой при поиске кратчайших путей. Это уменьшает общее время построения схемы сети дорог, упрощает процесс работы и позволяет учитывать географические особенности конкретного арендного участка. Кроме того, в основной части алгоритма происходит добавление дополнительных точек в граф, которые дают возможность строить пути не только по вершинам – выделам графа. Эти точки располагаются на ребрах – дорогах, которые уже включены в схему сети. После нахождения кратчайшего пути, все ненужные вспомогательные вершины удаляются из графа. Это уменьшает длину пути между нижним складом и центром выдела и позволяет приблизить схему сети к реальным условиям. На основе проведенных исследований может быть разработана методика проектирования рациональной схемы сети лесовозных дорог и определения экономической доступности лесных ресурсов.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Андреева, Л.П. Экономические основы устойчивого управления лесным фондом Красноярского края: монография [текст] / Л.П. Андреева, Е.Е. Моисеева, М.С. Селин. – Красноярск: СибГТУ, 2007. – 128 с.
Болотов, О.В. Основы расчета и планирования устойчивого управления лесопользованием: монография [Текст] / О.В.
Мохирев, Е.В. Горяева. – Красноярск: СибГТУ, 2005. – 183 с.
Гуров, С.В. Планирование транспортных систем лесных предприятий в условиях многоцелевого лесопользования [текст] / С.В. Гуров, Р.Н. Ковалев. – Екатиринбург: Урал. гос. техн. акад., 1996. – 250 с.
Кормен, Т. Х. Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS / Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1
Ливитин, А. В. Алгоритмы: введение в разработку и анализ = Introduction to The Design and Analysis of Aigorithms [текст] / А. В. Левитин. — М.: «Вильямс», 2006. — С. 349-353. — ISBN 0-201-74395-7
Мохирев, А.П. Обоснование проектирования сети лесных дорог на примере предприятий Нижнего Приангарья [текст]: дис. … канд. тех. наук: 05.21.01: защищена 15.12.07: утв. 03.10.07 / Мохирев Александр Петрович. - Красноярск: СибГТУ, 2007. – 169 с. - Библиогр.: с 159-169.
Романовский И.В. Дискретный анализ: Учебное пособие для студентов, специализирующихся на прикладной математике и информатике. — 3-е изд., перераб. и доп. — СПб.: Невский Диалект; БХВ - Петербург, 2003
Чижов, А.П. Совершенствование процессов лесопиления на основе картографирования сосняков Нижнего Приангарья [текст]: дис. … канд. тех. наук: 05.21.05: защищена 05.05.01: утв. 03.05.01 / Чижов Александр Петрович. – Красноярск: СибГТУ, 2001. – 200 с. – Библиогр.: с 185-200.