Алгоритм распределения учебной нагрузки между преподавателями кафедры и оценка качества распределения
Тархов С.В., Султанова С.Н.
Введение
Распределение учебной нагрузки между преподавателями кафедры является сложной организационнотехнической задачей. В реальной ситуации решение плохо-формализуемой многокритериальной оптимизационной задачи, какой является задача распределения учебной нагрузки, не позволяет системе работать в автоматическом режиме, поэтому необходимым является использования человеко-машинных процедур.
Основной целью решения данной задачи является обеспечение качественного и рационального распределения.
Для ее решения была разработана постановка многокритериальной оптимизационной задачи. Предложена
математическая модель, которая позволяет, учитывая критерии и ограничения получать множество
допустимых вариантов распределения [1] и функциональная модель (построенная на базе методологии
SADT) дающая возможность последовательно представить компоненты исследуемой автоматизированной
информационной системы поддержки принятия решений Учебная нагрузка
профессорско-преподавательского состава
и саму структуру системы [2].
Математическая и функциональная модели построены таким образом, что они не предусматривают полностью автоматического поиска решений.
Система является человеко-машинной и предусматривает активное участие лица, принимающего решения (ЛПР) в процессе решения задачи распределения учебной нагрузки. Важно, что система позволяет ЛПР поэтапно анализировать проблему и вырабатывать свои предпочтения в процессе интерактивной работы с системой. На наш взгляд, именно такая человеко-машинная система помогают ЛПР наиболее качественно и рационально распределять учебную нагрузку.
В работе [3] был предложен подход к решению задачи распределения учебной нагрузки между преподавателями кафедры, позволяющий представлять полученные варианты распределения в виде нечеткой случайной величины (НСВ) и, исходя из формы НСВ, оценивать их.
В данной работе рассматриваются алгоритмы распределения учебной нагрузки между преподавателями кафедры и подходы к оценке качества распределения на основе разработанными авторами математической модели и функциональной модели.
Алгоритм распределения
Выделим в первую очередь наиболее крупные этапы решения задачи (подзадачи) распределения учебной нагрузки между преподавателями кафедры и изобразим порядок выполнения их в виде схемы, называемой укрупненной (рис. 1).
Решение поставленной задачи состоит из пяти основных этапов:
- ввода исходных данных;
- закрепления за преподавателями видов учебных работ;
- оценка распределения и формирование вариантов распределения;
- сравнение вариантов распределения и выбор наилучшего варианта распределения;
- вывод наилучшего варианта распределения.
Блоки 1 – 10 реализуют первый этап формирования исходных данных для последующего распределения учебной нагрузки.
В блоке 2 вводятся следующие исходные данные для решения задачи:
- учебная нагрузка кафедры по читаемым ей дисциплинам, рассчитанная учебным управлением;
- плановый штат, рассчитанный учебным управлением;
- фактические данные о преподавателях (фактический штат).
В блоке 3 вводятся общие ограничения: ассистент не должен читать лекции; каждый преподаватель может вести нагрузку, не превышающую максимальной нагрузки допустимой трудовым законодательством и т.д. Ограничения могут носить как качественный, так и количественный характер.
В блоке 4 вводятся следующие критерии: максимальная полезность
, минимальное среднее
квадратичное отклонение учебной нагрузки преподавателя, максимальная преемственность,
максимальное предпочтение преподавателей и др. Количество критериев и их содержательная часть
могут изменяться, добавляться по мере необходимости. Критерии и ограничения предписывают
условия выполнения необходимых преобразований.
Блок 5 предназначен для определения средних показателей: средней нагрузки по кафедре, средней
нагрузки по должностям преподавателей, средней нагрузки преподавателей по конкретному виду
учебной
работы, необходимых для распределения нагрузки. Средняя нагрузка по кафедре рассчитывается из
соотношения: учебная нагрузка кафедры к фактическому штату
, а средняя нагрузка по
должностям преподавателей – с учетом принятых коэффициентов.
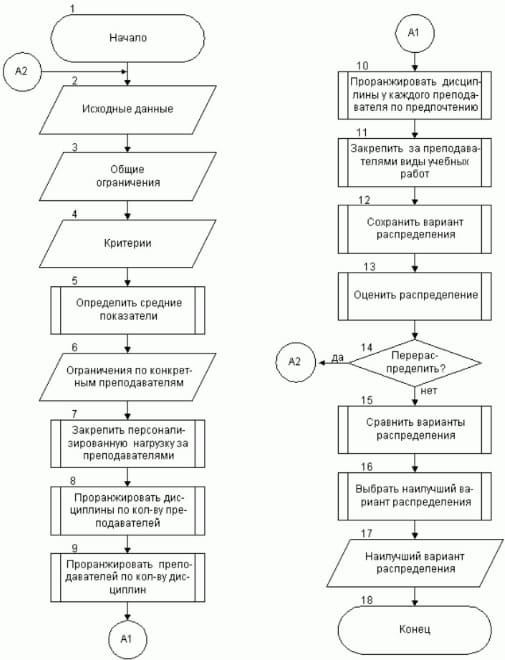
Рис. 1. Укрупненная схема алгоритма распределения учебной нагрузки между преподавателями кафедры
Для того чтобы определить среднюю нагрузку преподавателей по конкретному виду учебной работы необходимо сложить всю учебную нагрузку по конкретному виду работы и разделить на число преподавателей, имеющих право вести занятия по данному виду учебной работы.
Блок 6 позволяет вводить ограничения по конкретному преподавателю (индивидуальные объемы часов), например, у одного из преподавателей учебная нагрузка не должна превышать 500 часов, а другому преподавателю необходимо снизить учебную нагрузку в первом семестре и др.
Одна часть ограничений вводится как исходные данные, другая часть рассчитывается из средних показателей.
В блоке 7 в первую очередь, если есть персонализированная нагрузка, жестко закрепляем ее за преподавателями, которые ее должны вести. Персонализированной является нагрузка по следующим видам учебных работ: руководство всеми видами практик с проверкой отчетов и приемом зачетов; руководство, консультации, рецензирование выпускных квалификационных работ специалистов и магистерских диссертаций и участие в работе ГАК; руководство, консультации, рецензирование выпускных квалификационных работ бакалавров и участие в работе ГАК; руководство магистрантами; руководство аспирантами и докторантами; и т.д. В разных учебных заведениях приведенная структура персонализированной нагрузки может отличаться от описанной выше.
Закрепленная персонализированная нагрузка позволяет однозначно показать, кому из преподавателей она должна быть назначена, так руководство кафедрой – только заведующему кафедрой, руководство аспирантами – за конкретными преподавателями и т.д.
Блоки 8-10 позволяют выявить на основе ранжирования критические параметры.
- По дисциплинам (рис. 2) – дисциплины проранжированы по количеству преподавателей, которые их могут вести.
- По преподавателям (рис. 3) – преподаватели проранжированы по количеству дисциплин количеству, которые они могут вести.
- По учебной нагрузке (рис. 4) – дисциплины у каждого преподавателя проранжированы по предпочтению.
На втором этапе осуществляется закрепление учебной нагрузки за преподавателями по видам работ (блок 11). Он представляет достаточно сложный и самостоятельный фрагмент распределения, поэтому его целесообразно выделить в отдельную задачу. В процессе решения поставленной задачи закрепление выполняется в указанной последовательности:
- закрепления за преподавателями лекций, экзаменов, текущих консультаций и экзаменационных консультаций;
- закрепления за преподавателями практических занятий и практических работ;
- закрепления за преподавателями других видов учебных работ (контрольные работы, курсовые работы и т.д.).
На третьем этапе в блоках 12 – 14 производится оценка распределения и формирование вариантов распределения.
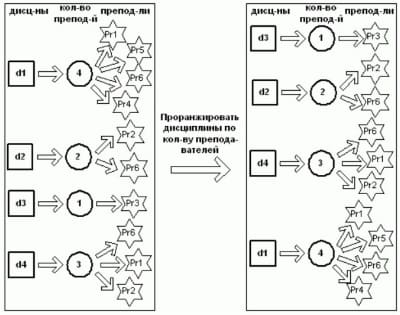
Рис. 2. Ранжирование дисциплин
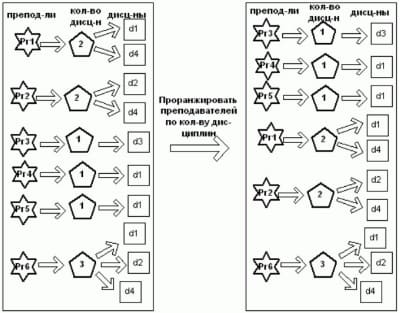
Рис. 3. Ранжирование преподавателей
В блоке 14 проверяется условие о том, нужно ли перераспределить учебную нагрузку (распределение нового варианта). Если хотим получить новое распределение, переходим в блок 2 и, изменяя, например, некоторые предпочтения, ограничения преподавателя, среднюю нагрузку преподавателя, соотношения, фактические данные о преподавателях повторяем все действия до блока 14, если нет, то переходим к блоку 15.
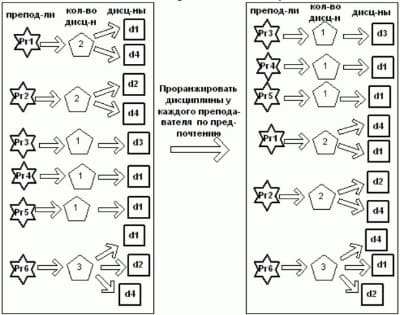
Рис. 4. Ранжирование дисциплин у каждого преподавателя по предпочтению
Условные обозначения, принятые на рис. 2-4:

Четвертый этап позволяет сравнивать варианты распределения и выбирать наилучший вариант распределения из множества допустимых вариантов распределения (блоки 15 – 16).
Наконец, в блоке 17 выводиться наилучший вариант распределения, выбранный экспертом, и завершается алгоритм распределения.
Оценка качества распределения
Использование предлагаемого алгоритма распределения учебной нагрузки между преподавателями кафедры не дает однозначного решения и приводит к некоторому множеству вариантов распределения.
Для сравнительной оценки полученных вариантов введем в рассмотрение следующие критерии:
- Критерий среднего квадратичного отклонения (критерий равномерности) учебной нагрузки преподавателя. Под равномерностью будем понимать как относительно равное количество часов учебной нагрузки каждого преподавателя, как в осенний, так и в весенний семестр, так и относительно равную суммарную учебную нагрузку преподавателей в семестр.
- Критерий
полезности
(по качественному составу). Необходимо учитывать при распределении учебной нагрузки не только профессиональную подготовку преподавателя, но и квалификацию, и опыт работы, связанные с выполнением каждого преподавателя всех видов учебных работ конкретных дисциплин. - Критерий преемственности. Необходимость введения его вызвана тем, что, учитывая опыт работы преподавателей по чтению конкретных дисциплин, позволяет улучшить качество обучения. Он отражает положение о том, что процесс обучения происходит наиболее качественно, так как если преподаватель читал эту дисциплину, то студентам будет намного легче усвоить материал.
- Критерий максимального удовлетворения предпочтений преподавателей при распределении (степень удовлетворенности преподавателей). Принцип наибольшего удовлетворения максимального числа преподавателей, хотя при этом, возможно, что какие-то распределения получатся в ущерб некоторым субъективным интересам преподавателей, отражающие интересы кафедры, за счет других Именно этот принцип в наибольшей степени соответствует содержанию задачи о назначениях [4].
Используя алгоритмы оценки эффективности качества (критерии качества распределения), можно произвести оценку каждого распределения.
Для этого определим с помощью метода линейной свертки критериев связь между полезностью альтернативы и значениями критериев:
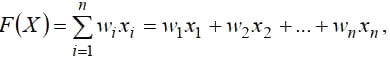
где wi – вес (важность) i-го критерия, назначаемый ЛПР; xi – оценка альтер-нативы X по i-му критерию.
Как правило, веса критериев wi выбираются таким образом, чтобы их сумма равнялась единице. В этом случае оценка альтернативы x i попадает в границы балльной шкалы, в которой измерены критерии. Один из возможных формальных способов решения многокритериальных задач заключается в том, что предварительно упорядочивают критерии по важности, а затем последовательно решают несколько оптимизационных задач (число задач равно числу критериев) в порядке убывания важности критериев.
Если после упорядочивания критериев по важности оказывается, что первый критерий К1 существенно важнее всех остальных, критерий К2 намного важнее всех критериев, кроме К1, критерий К3 существенно важнее всех, кроме К1 и К2, и т. д., то естественно считать, что i-ое решение лучше j-го решения, когда это i-ое решение лучше j-го по критерию К1. Если i-oe и j-ое решения эквивалентны по К1, то предпочтение отдается лучшему по критерию К2, и т. д. Такое упорядочение, называемое лексикографическим, возможно лишь при значительной неравноценности критериев. В приводимой таблице дается пример такого упорядочивания пяти альтернатив А1, ..., A5 по четырем критериям К1, ..., К4. В клетках – значения aij для i-ой альтернативы по j-му критерию.
Таблица 1. Результаты многокритериального оценивания
|
A |
K |
|||
|
K1 |
K2 |
K3 |
K4 |
|
|
A1 |
0,4 |
0,2 |
0,3 |
0,1 |
|
A2 |
0,3 |
0,2 |
0,2 |
0,3 |
|
A3 |
0,3 |
0,4 |
0,1 |
0,2 |
|
A4 |
0,3 |
0,1 |
0,2 |
0,4 |
|
A5 |
0,5 |
0,2 |
0,1 |
0,2 |
Показатели распределения позволят наглядно посмотреть варианты распределения в виде диаграмм или графиков (рис. 5).
На основе полученных показателей качества распределения лицо, принимающее решение (эксперт) выбирает наилучший (наиболее рациональный, приемлемый) вариант распределения учебной нагрузки преподавателей (рис. 6). При этом нет оснований утверждать, что лучший из выбранных вариантов является действительно оптимальным, т.е. лучшим из всех возможных. Более того, обычно получается, что max Ki < max Kj. Поэтому в этой задаче, как и в других многокритериальных задачах, будет говорить не об оптимальных решениях, а об эффективных или наилучших. Под эффективными решениями будем понимать такие решения, которые не могут быть улучшены сразу по всем критериям.
Заключение
Предложенный алгоритм позволяет: наиболее качественно и рационально распределить учебную нагрузку между преподавателями кафедры; сформировать множество вариантов распределения ; используя критерии качества распределения, производить оценку каждого распределения.
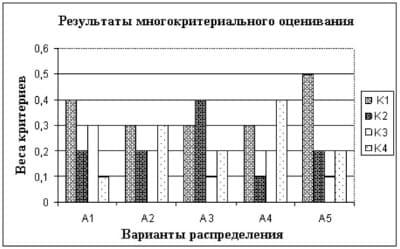
Рис. 5. Показатели качества распределения
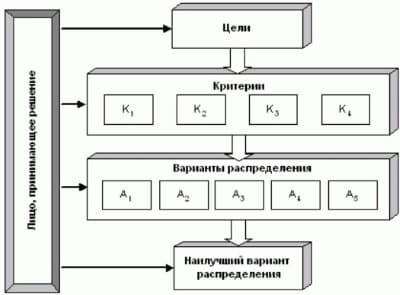
Рис. 6. Поиск наилучшего варианта распределения учебной нагрузки
На основе полученных показателей качества вариантов распределений лицо, принимающее решение (эксперт), выбирает наилучшее с его точки зрения решение по распределению учебной нагрузки преподавателей с учетом ряда критериев и множества ограничений.