УДК 004.021
Оригинал: Comparative Study of Multiobjective Genetic Algorithms
Сравнительный анализ многокритериальных генетических алгоритмов
Авторы: Cîrciu M.S., Leon F.
Перевод: Липова Э.Е.
1. Вступление
Эволюционные алгоритмы
- это общий термин, используемый для обозначения любого
алгоритма стохастического поиска, который использует механизмы, вдохновленные биологической
эволюцией и генетическими операторами, такими как мутация, кроссовер (скрещивание), отбор и
выживание наиболее приспособленных.
Предлагаемые решения оптимизационной задачи играют роль особей в популяции. Решения с высокой приспособленностью будут иметь более высокую вероятность выжить и будут воспроизводить лучшие решения эволюционного процесса.
Существует три основных типа эволюционных алгоритмов: генетические алгоритмы, эволюционные стратегии и эволюционное программирование. Все три были разработаны независимо, но общие принципы одинаковы.
Они развивают популяцию кандидатов для решения поставленной задачи, чтобы найти оптимальные решения, используя операторы, взятыми из естественного генетического разнообразия (создание новых особей через кроссовер и мутацию), естественного отбора и выживания наиболее приспособленных (конкуренция за воспроизводство и ресурсы среди особей).
Однако каждый тип имеет несколько вариаций из-за различных первоисточников и областей решаемых задач. Генетические алгоритмы используют кроссовер и мутацию, и подходят для задач оптимизации.
Эволюционные стратегии используют вещественные параметры. Сначала эволюционные стратегии не использовали оператор кроссовер, позже он был введен. Поэтому их структура аналогична структуре генетических алгоритмов с вещественными параметрами.
Многокритериальной задачи обычно сложнее и находят много применений в реальных жизненных ситуациях.
Статья организована следующим образом. В разделе 2 представлен обзор генетических алгоритмов. В разделе 3 описаны три алгоритма, используемые для сравнения: весовой генетический алгоритм, VEGA и NSGA-II. Наконец, в разделе 4 проиллюстрированы некоторые тематические исследования с тремя специально разработанными задачами многокритериальной оптимизации, используемыми для сравнения производительности исследуемых алгоритмов.
2. Генетический алгоритм
Многие проблемы реального мира предполагают одновременную оптимизацию множества целей, зачастую противоречивых. В задаче многокритериальной оптимизации, невозможно найти наилучшее решение, достигнув всех целей. Решение может быть оптимальным в отношении одной цели, но неудовлетворительным для другой. Цель состоит в том, чтобы найти множество оптимальных решений, известных как Парето-оптимальное множество. Эти решения являются оптимальными потому, что никакие другие решения в области поиска не удовлетворяют все цели. Поскольку ни одно из решений в наборе не является лучшим, чем любое другое решение, в отношении всех целей любое из них является приемлемым решением.
Многокритериальный генетический алгоритм может быть модифицированной версией простого генетического алгоритма, предназначенного для решения многокритериальной задачи оптимизации. Возможность использования эволюционных алгоритмов решения многокритериальной задачи оптимизации была предложена Розенбергом в его диссертации [1]. Он предложил использовать генетический алгоритм в химии для поиска популяции одноклеточных организмов с несколькими свойствами или целями. Поскольку генетический алгоритм работает с популяцией решений-кандидатов, для настройки поиска в сторону Парето-оптимального фронта могут использоваться критерии доминирования, и несколько Парето-оптимальных решений могут быть получены за одну итерацию. Что является основной причиной использования генетических алгоритмов для многоцелевой оптимизации [2].
Генетические алгоритмы работают с набором хромосом, называемого популяцией. Популяция инициализируется случайным образом. По мере работы поиска наилучшего решения популяция включает в себя все лучшие и лучшие решения, а затем она сходится, что означает, что в ней доминирует одно решение [3]. Однако простой может обеспечить только одно решение для данной комбинации весов, в отличие от MOGA, который может предоставить набор решений.
2.1. Структура Генетического Алгоритма
Считается, что длина и число используемых хромосом постоянны и популяция P(t+1) в момент времени t+1 получается путем взятия всех потомков популяции P (t) и последующего удаления хромосом предыдущего поколения [4].
Структура генетического алгоритма следующая:
Шаг 1: t ← 0;
Шаг 2: инициализируйте популяцию P (t) со случайными значениями;
Шаг 3: Оцените хромосомы из популяции P (t). Для этого используется фитнесс-функция для поставленной задачи;
Шаг 4: пока условие остановки не выполнено совершите следующие действия:
Шаг 4.1: выберите хромосомы из P (t) для нового поколения. Пусть P1 - набор выбранных хромосом (промежуточная популяция).
Шаг 4.2: применить генетические операторы к хромосомам из пула рекомбинации P (t) (кроссовер и мутация). Пусть P2 - полученная популяция, т. е. потомство популяции P (t). Удалить из P1 потомство родителей. Хромосомы, оставшиеся в P1, включаются в P2. Построение нового поколения: P(t+1) ← Р2; удалить хромосому от P(t); t ← t+1; оценки Р (t). Обычно условием остановки является достижение заданного числа поколений, хотя существуют и другие условия, которые проверяют сходимость ГА путем оценки фитнесс-функции популяции. Результатом работы алгоритма является лучшая особь из последнего поколения. Нет гарантии, что лучшая особь передаст свои гены следующему поколению. Поэтому полезно сохранить лучшую особь в каждом поколении, такой процесс называется элитизмом.
2.2. Многокритериальные Генетические Алгоритмы
В отличие от однокритериальной оптимизации, в многокритериальной фитнесс-функция и отбор должны удовлетворить несколько целей. Таким образом, многокритериальные алгоритмы отличаются от простого генетического алгоритма тем, как работает функция приспособления и выборка. Было введено несколько различных вариантов многокритериальных алгоритмов. Основываясь на фитнесс-функциях и отборе, многокритериальные алгоритмы можно классифицировать как подход, основанный на агрегации, популяции и Парето [2].
Первый многокритериальный генетический алгоритм, векторный генетический алгоритм (VEGA), был предложен Шаффером [8]. Затем, были разработаны такие многокритериальных эволюционные алгоритмов: Multiobjective Genetic Algorithm (MOGA), Niched Pareto Genetic Algorithm (NPGA), Weight-based Genetic Algorithm (WBGA), Random Weighted Genetic Algorithm (RWGA), Non-dominated Sorting Genetic Algorithm (NSGA), Strength Pareto Evolutionary Algorithm (SPEA), Pareto-Archived Evolution Strategy (PAES), Fast Non-dominated Sorting Genetic Algorithm (NSGA-II). Хотя существует множество вариаций многокритериальных генетических алгоритмов, приведенные алгоритмы хорошо известны и заслуживают доверия. Они использовались во многих приложениях, и их эффективность была проверена в нескольких исследованиях. Как правило, многокритериальные генетические алгоритмы различаются в зависимости от их фитнесс-функции, элитарности или диверсификации [3].
В данном исследовании рассмотрены три алгоритма: весовой генетический алгоритм, VEGA и NSGA-II. Далее описан каждый из трех алгоритмов.
3. Классы многокритериальных генетических алгоритмов
3.1. Весовой Генетический Алгоритм
Поскольку простой генетический алгоритм основан на скалярной функции для управления поиском наилучшего решения, наиболее интуитивным подходом для использования генетического алгоритма для задачи многокритериальной оптимизации является объединение всех целей в одну объективную задачу с использованием одного из традиционных методов агрегирующих функций. Затем для решения задачи используется простой генетический алгоритм. Примером такого подхода является линейная сумма весов, которая состоит из сложения всех целевых функций вместе с использованием различных весов для каждого из них. Таким образом, задача многокритериальной оптимизации преобразуется в скалярную
задачу оптимизации вида: 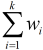 где,
wi-весовые коэффициенты, представляющие относительную значимость целей. Как правило,
где,
wi-весовые коэффициенты, представляющие относительную значимость целей. Как правило, 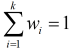 [2].
[2].
Даже если идея алгоритма проста, вводится сложный вопрос. Какие значения весов нужно использовать? Конечно, однозначного ответа на этот вопрос нет. Ответ зависит от важности каждой цели в контексте проблемы. Вес цели обычно выбирается пропорционально ее важности.
Этот метод не требует никаких изменений в механизме простого генетического алгоритма. Поэтому он прост, эффективен и легок в реализации. Он может быть использован для решения простых задач многокритериальной оптимизации с несколькими целевыми функциями и выпуклой области поиска. Метод страдает от следующих проблем [2]: оптимальное решение Парето специфично для параметров фитнес-функции, используемых при преобразовании задачи многокритериальной оптимизации в единую задачу оптимизации. Чтобы найти различные Парето-оптимальные решения, необходимо изменить параметры и решить новую задачу. Таким образом, для нахождения n различных Парето-оптимальных решений необходимо сформировать и решить n различных одноцелевых оптимизационных задач. Другим недостатком является то, что метод чувствителен к выбору весов и требует от пользователя знаний о задаче для генерации правильных параметров.
Основным недостатком является то, что для некоторых задач, которые демонстрируют невыпуклый Парето-оптимальный фронт, этот подход не может найти все решения, независимо от того, как выбраны веса.
Однако этот алгоритм легче реализовать, чем конкретные алгоритмы многокритериальной оптимизации, и если известна важность каждой цели, то подходит такой метод поиска приемлемых решений.
3.2. Векторно-оценочный генетический алгоритм (VEGA)
VEGA является первым генетическим алгоритмом, используемым для аппроксимации оптимального множества Парето множеством не доминированных решений; он был реализован Шаффером [8]. Это название подходит для многокритериальной оптимизации, поскольку алгоритм вычисляет целевой вектор.
VEGA является прямым развитием простого генетического алгоритма для многокритериальной оптимизации. Поскольку ряд задач (M) должен быть обработан, Шаффер в каждой итерации случайным образом делит популяции генетического алгоритма на M равных субпопуляций. Каждой субпопуляции присваивается фитнес-функция, основанная на другой целевой функции. Таким образом, каждая из M целевых функций используется для оценки некоторых членов популяции.
Этот алгоритм выделяет решения, которые оптимальны для отдельных целевых функций. Шаффер использует оператор пропорционального выбора. Чтобы найти промежуточные решения, Шаффер разрешил пересечение между любыми двумя решениями во всей популяции. Таким образом, кроссовер между двумя удовлетворительными решениями, каждое из которых соответствует своей цели, может найти потомство, которое является хорошим компромиссным решением. Мутация применяется к каждой особи, как обычно.
Критика VEGA [7] включает следующие аргументы. VEGA очень проста и легка в реализации, потому что изменяется только механизм отбора. Одним из основных преимуществ является возможность генерировать несколько решений за один запуск алгоритма. Однако, перетасовка и слияние всех субпопуляций, которые выполняет VEGA, соответствует усреднению компонентов приспособления, связанных с каждой из целей. Поскольку Шаффер использует пропорциональное назначение фитнесс-функции, эти компоненты, в свою очередь, пропорциональны самим целям. Таким образом, полученная ожидаемая приспособленность соответствует линейной комбинации целей, где веса зависят от распределения популяции в каждом поколении. Значит, VEGA имеет те же проблемы, что и ранее рассмотренный алгоритм.
3.3. Быстрый недоминируемый генетический алгоритм на основе сортировки (NSGA-II)
NSGA-II был предложен Сринивасом и Деб [9]. В данном исследовании рассматривается усовершенствованная версия NSGA, называемая NSGA-II, которой является быстрым многокритериальным алгоритмом с элитарностью, предложенный Деб и соавторами [6] для устранения недостатков NSGA. Основные особенности NSGA-II, такие как низкая вычислительная мощность, сохранение меньшего разнообразия параметров, элитарность и представление реальных значений, описаны в следующей работе [2].
Низкая вычислительная мощность: NSGA-II требует не более O(mN2) вычислительной мощности, которая ниже по сравнению с O(mN 2) NSGA. Процедура поиска не доминирующего фронта, используемая в NSGA-II, аналогична процедуре сортировки без доминирования, предложенной Гольдбергом [5], за исключением того, что для повышения ее эффективности используется лучшая бухгалтерская стратегия. В этой бухгалтерской стратегии каждое решение от популяции сравнивается с частично заполненной для доминирования популяцией, а не с каждым решением в популяции, как в NSGA. Первоначально первое решение из популяции хранится в множестве P’. Затем каждое решение i сравнивается со всем решением в P’ по одному. Если решение i доминирует над любым решением j из P’, то решение j удаляется из P’. В противном случае, если в решении i доминирует любое решение j в P’, то решение игнорируется. Если в решении i не доминирует какое-либо решение в P’, то оно сохраняется в P’. Поэтому множество P’ растет с не доминирующими решениями. Когда все множество решений проверяется, решения в P’ составляют не доминирующее множество. Чтобы найти другие фронты, не доминирующие решения в P’ будут уменьшены от P, и процедура повторяется до тех пор, пока все решения в P не будут ранжированы.
Сохранение разнообразия: для поддержания разнообразия среди решений, NSGA-II заменяет подход совместного использования приспособления в NSGA с переполненным подходом сравнения, который не требует каких-либо пользовательских параметров. В подходе полного сравнения каждое решение в популяции имеет два атрибута: не доминирующий ранг (irank) и расстояние плотности (idistance). Расстояние плотности решения i служит оценкой размера самого большого кубоида, охватывающего точку i без включения в популяцию другой точки.
Рис. 1 [2] иллюстрирует вычисление расстояния плотности для решения i в его передней части, которое является средней длиной стороны для кубоида, охватывающего решение i (показано с помощью пунктира).
Оператор выбора переполненного турнира, который используется для направления поиска к распределенному
Парето-оптимальному фронту, определяется следующим образом [2]: решение i выигрывает турнир
с другим решением j, если решение i имеет лучший ранг
(irank < jrank) или i
и j имеют тот же ранг, но решение i имеет лучшее расстояние плотности, чем решение
j (irank = jrank и
idistance > jdistance). Если
i и j имеют одинаковый ранг и одинаковое расстояние вытеснения, то один из них
случайным образом выбирается в качестве победителя. 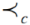 является
оператором сравнения переполнения и формально определяется как i
является
оператором сравнения переполнения и формально определяется как i 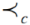 j если (irank <
jrank) или (irank =
jrank и idistance >
jdistance).
j если (irank <
jrank) или (irank =
jrank и idistance >
jdistance).
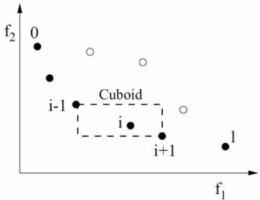
Рис. 1 - Расчет расстояния плотности.
Элитарность в NSGA-II обеспечивается путем сравнения текущей популяции с ранее найденными лучшими не доминирующими решениями (сохраненными в P’) и путем объединения родительской и дочерней популяций для формирования комбинированной популяции с размером 2N. Затем объединенная популяция сортируется в соответствии с не доминированием. Лучшие решения - это решения, принадлежащие потомству без доминирующего фронта F1. Если размер F1 меньше N, то для новой совокупности выбираются все решения в F1. Остальные решения новых популяций выбираются из подпоследовательности не доминирующих фронтов в порядке их ранжирования F2, F3 и так далее. Эта процедура продолжается до тех пор, пока не будут выбраны N решений для новой совокупности. Чтобы выбрать ровно N членов, решения в последнем фронте сортируются с помощью оператора сравнения в порядке убывания.
Рис. 2 [2] иллюстрирует эту процедуру. Новая популяция теперь используется для отбора, скрещивания и мутации, чтобы создать новую популяцию размера N [2], [6].
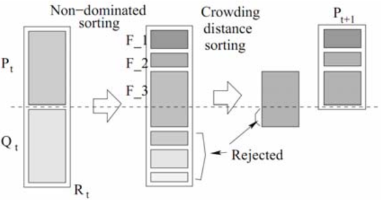
Рис. 2 - Элитарность в NSGA-II
Вещественное представление: NSGA-II поддерживает вещественное представление, в котором хромосома представлена в виде вектора переменных в вещественных числах. Используя вещественное представление, NSGA-II может достичь произвольной точности в полученных решениях (точность будет зависеть от машины), и он может обрабатывать проблемы, имеющие непрерывную область поиска решения. В реальных генетических алгоритмах основная проблема заключается в том, как создать новую пару векторов потомства из пары реально значимых родительских векторов и как их мутировать [2]. NSGA-II использует арифметический кроссовер, который линейно объединяет две родительские хромосомы для получения двух потомков, как показано в следующих уравнениях, где a-действительное число между 0 и 1:
- (1)offspring1 = a parent1 + (1 – a) · parent2
- (2)offspring2 = (1 – a) · parent1 + a parent2
Оператор мутации заменяет значение всех генов равномерно распределенным случайным значением в диапазоне, указанном пользователем.
Разнообразие среди не доминирующих решений вводится с помощью процедуры сравнения плотности, которая используется в отборе турнира на этапе сокращения популяции. Поскольку решения конкурируют с их расстоянием плотности, не требуется никакого дополнительного параметра. Хотя расстояние вытеснения вычисляется в области результата целевой функции, оно также может быть реализовано в области параметров [6].
4. Исследование конкретной ситуации
Есть несколько особенностей, которые могут вызвать трудности для многоцелевых генетических алгоритмов в сходящемся к оптимальному Парето фронту и поддержании разнообразия в пределах популяции. Мультимодальность, обман и изолированные оптимумы - известные проблемы в одноцелевой оптимизации. Определенные характеристики Парето-оптимального фронта могут помешать многокритериальному алгоритму находить разнообразные Парето-оптимальные решения: не выпуклость, дискретность и неравномерность. Предложенные тестовые функции, используемые в данном исследовании, отражают эти проблемы.
Каждый тест рассматривает две цели, каждая из которых требует минимизации другой целевой функции.
4.1. Выпуклый Парето-Оптимальный Фронт
Первый набор тестовых функций имеет выпуклый Парето-оптимальный фронт, когда целью является одновременная минимизация функций f и h:
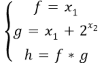
В каждом алгоритме использовались следующие параметры: размер популяции: N=200, количество поколений: G=100, частота мутаций: pm= 0.03 и частота кроссоверов: pc =0.9.
Не доминированные решения, полученные по каждому алгоритму, показаны на рис. 3. Для WBGA веса выбирались в интервале [0,1], и для каждой комбинации выполнялось несколько пробегов.
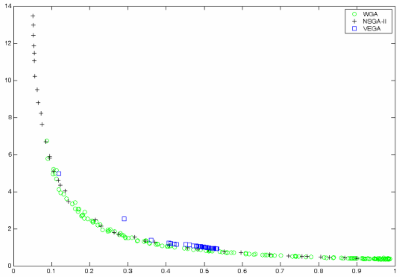
Рис. 3 - Недоминированные решения, полученные для задачи с выпуклым Парето-оптимальным фронтом.
Для выпуклого фронта все алгоритмы получают хорошую аппроксимацию Парето-оптимального фронта.
4.2. Вогнутый Парето-Оптимальный Фронт
Второй набор тестовых функций имеет невыпуклый Парето-оптимальный фронт:
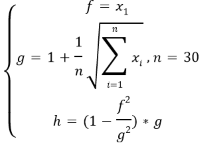
Алгоритмы используют те же параметры, что и раньше. Решения без доминирования, полученные по каждому алгоритму, визуализируются на рис. 4.
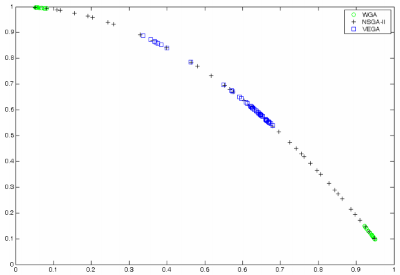
Рис. 4 - Недоминируемых решений, полученных для задачи с вогнутым Парето-оптимальным фронтом.
NSGA-II и VEGA получают хорошее приближение Парето-оптимального фронта. Однако весовой генетический алгоритм не может найти промежуточные решения.
4.3. Прерывистый Парето-Оптимальный Фронт
Третий набор тестовых функций имеет прерывистый Парето-оптимальный фронт:
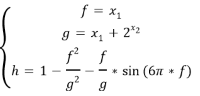
Введение синусоидальной функции вызывает разрыв в Парето-оптимальном фронте, хотя в области параметров разрыва нет. Каждый алгоритм использует те же параметры, что и раньше. Недоминированные решения, полученные по каждому алгоритму, показаны на рис. 5.
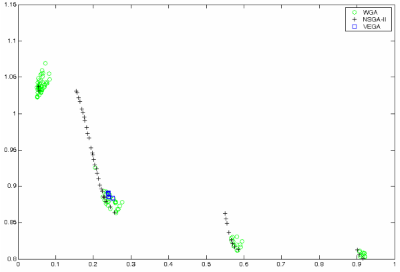
Рис. 5 - Недоминированные решения, полученные для задачи с разрывным Парето-оптимальным фронтом.
Для этой задачи только NSGA-II аппроксимирует правильный Парето-оптимальный фронт. Весовой генетический алгоритм может найти некоторые кластеры решений в окрестности истинных фронтов Парето. В этом случае VEGA не содержит хороших решений.
5. Выводы
Весовой генетический алгоритм хорошо работает на выпуклом фронте, но имеет трудности на неоднородном или вогнутом фронте. Еще одна трудность заключается в выборе весов, что требует от пользователя знания о проблеме. Алгоритм получает одно конечное решение, таким образом, чтобы найти различные оптимальные решения Парето, алгоритмы должны выполняться с несколькими наборами весов.
VEGA превосходит производительность взвешенного генетического алгоритма. Проблема для этого алгоритма заключается в том, что из-за задания фитнес-функции конечные решения имеют тенденцию сходиться к оптимальным значениям каждой задачи и “теряют” средние решения. Отмечается, что среди конечных решений доминируют решения, которые при реализации функции сортировки без доминирования удаляются ложные решения.
NSGA-II является наиболее эффективным алгоритмом, превосходит производительность обоих алгоритмов и получает хорошую аппроксимацию Парето-оптимального фронта независимо от его формы. Практические инженерные задачи включают в себя оптимизацию многозадачности, построенную на компромиссе. Все задачи требуют некоторой настройки генетических алгоритмов. Предполагается, что решения Парето, идентифицированные генетическими алгоритмами, будут сведены к репрезентативному небольшому набору для дальнейшего исследования проектировщиком или инженером. Поэтому для большинства реализаций жизненно важно не находить каждое Парето-оптимальное решение, а эффективно и надежно идентифицировать Парето-оптимальные решения по всему интересующему диапазону для каждой целевой функции.