Математическая модель распределения учебной нагрузки между преподавателями кафедры
Тархов С.В., Султанова С.Н.
Введение
В настоящее время методы и средства планирования и управления учебного процесса являются эффективным инструментом при реализации самых различных задач, таких как составление учебных планов, распределение учебной нагрузки, составлении расписаний и т.д. Распределение учебной нагрузки между преподавателями кафедры является одной из сложных и трудоемких (трудноразрешимых) задач, решаемых на этапе подготовки учебного процесса в вузе.
В зависимости от структуры кафедры, ее учебных занятий этот этап планирования может быть либо очень простым, либо достаточно сложным.
Особенно важен этот вопрос на кафедрах сложной структуры, ведущих большое число дисциплин с видами учебных занятий, имеющих много потоков по одной и той же дисциплине, большое число обслуживаемых факультетов, представительств, филиалов и видов обучения. Умение как можно более просто и оперативно распределять учебную нагрузку становится актуальным в наше время в условиях расширения вузов и многообразия форм обучения. В этом случае и возникают проблемы с распределением учебной нагрузки. Достигать этих целей на кафедрах со сложной структурой – достаточно трудоемкий процесс, и многое здесь зависит от того, какой метод положен в основу распределения учебной нагрузки.
Существуют два подхода к решению этой проблемы [1, 2]. Общими недостатками того и другого подхода являются выбор только одной целевой функции, что приводит к сужению нахождения оптимального варианта распределения, то, что они не учитывают различные ограничения, которые в свою очередь позволяют выбирать множество допустимых решений, расширяя возможность нахождения оптимального варианта распределения и т.д.
Один из подходов [1] предполагает решать задачу распределения учебных поручений между преподавателями кафедры с помощью метода целочисленного программирования. Такой подход обладает целым рядом явных недостатков. Вопервых, ограничение категориями должностей преподавательского состава: доцент (старший преподаватель) и ассистент (преподаватель) и требованиями к распределению учебных поручений между преподавателями кафедры, что влияет не только на качество распределения, но и на рациональность распределения учебных поручений по преподавателям. Вовторых, поиск оптимального плана распределения, не формируя множество допустимых вариантов. В-третьих, использование одного критерия при выборе оптимального решения, тем самым, сужая выбор оптимального варианта распределения и т.д.
Второй подход [2] предполагает использование дискретного квадратичного программирования. Он в основном отвечает концепциям организации образовательного процесса не в высших, а в средних специальных учреждениях. При распределении в вузе объем нагрузки считается на семестр, они же используют недельную нагрузку, так обычно происходит в школах, техникумах, колледжах. Предложенный алгоритм расчета субоптимального плана распределения между профессорскопреподавательским составом кафедры не позволяет определить какой метод используется при распределении нагрузки. При формировании оптимального плана распределения используют один из критериев, что сужает выбор наилучшего решения.
Для того чтобы решить данную задачу недостаточно одного критерия оптимальности. В случае однокритериальной задачи всё решилось бы относительно просто: с использованием какого-либо хорошо отработанного математического метода. Постановка проблемы, соответствующая реальной ситуации, требует рассмотрения целого ряда критериев. Критерии, согласно которым выбирается оптимальный вариант распределения учебной нагрузки. Таких как качество обучения, равномерность распределения учебной нагрузки по семестрам, преемственность, предпочтения преподавателей.
Имеются множества разнородных целей, каждая из которых должна быть учтена при выборе оптимального решения. Поэтому наша задача сводиться к многокритериальной задаче о назначениях, а значит, для ее решения можно воспользоваться методами многокритериальной оптимизации [3]
Построение математической модели
Цель решения данной задачи – наиболее качественно и рационально распределить учебную нагрузку между преподавателями.
Определим математическую модель системы распределения учебной нагрузки между преподавателями
кафедры. Пусть за кафедрой закреплено s дисциплин и на кафедре работают n преподавателей. Каждая
дисциплина в свою очередь состоит из j видов учебных занятий. Известна для каждого преподавателя
полезность
(профессиональная подготовка преподавателя, квалификация, опыт работы)
witj , связанная с
выполнением t-го преподавателя j-го вида учебного занятия i-й дисциплины 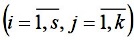 .
.
Обозначим xijt назначение j-го вида учебной нагрузки i-й дисциплины t -му преподавателю:

где 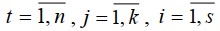
Требуется закрепить виды учебных занятий всех дисциплин за преподавателями так, чтобы при
максимальной полезности
, максимальной преемственности и максимальном предпочтении
минимизировать среднее квадратичное отклонение учебной нагрузки преподавателя при условии, что
из каждой дисциплины виды учебных занятий могут закрепляться только за одним преподавателем.
Таким образом, математическая модель поставленной задачи имеет следующий вид:
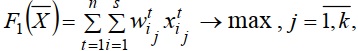 (1)
(1)
где wtij - комплексная оценка, связанная с выполнением t-го преподавателя j-го вида учебного занятия i-й дисциплины; xtij - назначение j-го вида учебного занятия i-й дисциплины t-му преподавателю.
Минимизировать среднее квадратичное отклонение учебной нагрузки преподавателя:
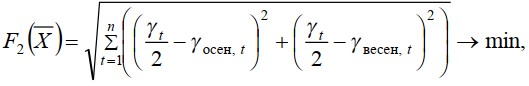
где γ t - нагрузка t-го преподавателя на учебный год; γосен, t - нагрузка t-го преподавателя в осенний семестр (период); γвесен, t - нагрузка t-го преподавателя в весенний семестр (период).
В каждом в вузе в основном учебный год подразделяется на два периода: осенний и весенний семестр, но в некоторых из них традиционно используется три периода. Применительно к нашему вузу мы имеем дело с двумя семестрами, хотя это не означает, что нашу модель нельзя будет использовать и с тремя периодами.
Или с тремя периодами:
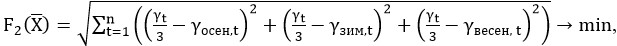 (2)
(2)
где γ зим, t - нагрузка t-го преподавателя в зимний период.
Если преподаватель читал эту дисциплину, желательно чтобы он про-должал ее читать (преемственность):
 (3)
(3)
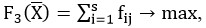
Для того чтобы максимизировать предпочтения преподавателей введем в рассмотрение степень предпочтения t-го преподавателя - lt
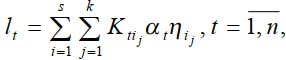
где Kti j - весовой коэффициент возможности t-го преподавателя вести j-й вид учебного занятия i-й дисциплины; αt - показатель индивидуальных особенно-стей t-го преподавателя; ηij - показатель желания вести j-й вид учебного занятия i-й дисциплины.
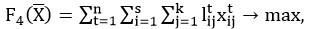 (4)
(4)
Ограничения:
Из каждой дисциплины виды учебных занятий могут закрепляться только за одним
преподавателем
:
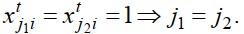 (5)
(5)
Каждый преподаватель может вести нагрузку, не превышающую максимальной нагрузки
допустимой трудовым законодательством
:
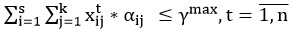 (6)
(6)
где αi j - норматив соответственно для чтения лекций, проведения практических занятий, лабораторных работ, зачета, экзамена, курсовой работы, дипломной работы и др. i-й дисциплины; γmax - рекомендуемая максимально допустимая нагрузка преподавателя по трудовому законодательству.
Доля нагрузки t-го преподавателя c-й категории должна находиться исходя из диапазонов
минимальной и максимальной нагрузки
:
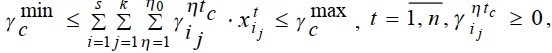 (7)
(7)
где γminc - рекомендуемая минимальная нагрузка
преподавателя c-й категории; 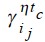 - доля нагрузки t-го
преподавателя c-й категории; γmaxcмаксимально
допустимая нагрузка преподавателя c-й категории.
- доля нагрузки t-го
преподавателя c-й категории; γmaxcмаксимально
допустимая нагрузка преподавателя c-й категории.
Один и тот же лекционный курс на одном потоке читается только одним
преподавателем
:
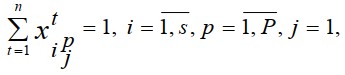 (8)
(8)
где p - индекс потока.
Аналогично записывается ограничение: желательно, чтобы практические занятия и
лабораторные работы на одном потоке назначались одному преподавателю
:
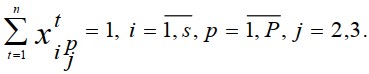 (9)
(9)
Можно предоставить преподавателю возможность самому задавать весовой коэффициент своих возможностей по каждому виду учебного занятия той или иной дисциплины. За него это может сделать лицо, принимающее решение в данном случае это заведующий кафедрой (заместитель по учебной работе) или созданная им экспертная группа. Хотя в принципе, возможно, что какие-то распределения получаться в ущерб некоторым субъективным интересам преподавателей, отражающие интересы кафедры.
Алгоритм принятия решения
Алгоритм принятия решения при наличии многих критериев можно представить так:
- Уяснение цели принятия решения.
- Определение множества допустимых альтернатив.
- Сравнение допустимых альтернатив и выбор наилучшего варианта решения.
Определим множество альтернативных вариантов решений Y = (Y1, Y2,…, Ym), из которых выберем оптимальное решение Y*.
Для осуществления выбора среди альтернативных вариантов сформулируем множество целей F =
(F1, F2,…, Fk). Характеристиками целей являются
критерии достижения целей и показатели достижения целей, например,
F1-максимальная полезность
, F2 – минимальное
среднее квадратичное отклонение учебной нагрузки преподавателя, F3 - максимальная
преемственность, F4 – максимальное предпочтение преподавателей и т.д.
Принятие решения по выбору преподавателя всегда осуществляется в условиях различных ограничений. Поэтому мы сформулировали четко множество ограничений (5)-(9) (A = (A1, A2,…, A5)), позволяющее еще на этапе формирования вариантов решений отбросить те из них, которые явно неприемлемы с точки зрения поставленных целей. Ограничения могут носить как качественный, так и количественный характер. Таким образом, множество альтернативных решений сужается до множества допустимых решений.
Для решения данной математической модели необходимо определить опорный план X = { xitj } → max (min). Для того чтобы некоторый план полученной задачи распределения был оптимальным, будем использовать методы многокритериальной оптимизации и метод ветвей и границ. Для задач такого типа такие методы наиболее эффективны.
Метод ветвей и границ позволяет выбирать из множества альтернативных решений по определенным признакам наиболее перспективные варианты распределения, отбросив бесперспективные. На основе них, используя методы многокритериальной оптимизации и эвристические процедуры, лицо, принимающее решение (эксперт), находит компромиссные, и наиболее приемлемые с его точки зрения, варианты распределения учебной нагрузки. На основе чего и выбирается наиболее качественное, рациональное решение.
Заключение
Рассмотренная математическая модель позволяет наиболее качественно рационально распределить учебную нагрузку между преподавателями кафедры. Приведенные ограничения дают возможность в процессе распределения получать множество допустимых решений, отбросив еще на этапе формирования вариантов те из них, которые явно неприемлемы с точки зрения поставленных целей, что позволяет расширить возможность нахождения оптимального варианта распределения.