УДК 519.8

Оптимизационные задачи являются частью многих областей современной науки и техники. Большинство таких задач на практике являются многокритериальными, при этом количество факторов настолько велико, что требует применение вычислительной техники, поэтому развитие процедур многокритериальной оптимизации имеет большое значение.

Многокритериальная оптимизация, также известная как векторная оптимизация [1], может быть определена как задача нахождения вектора переменных – решений, которые доставляют оптимум вектор-функции, чьи элементы представляют собой целевые функции. Эти функции формируют математическое описание представления критериев, которые обычно находятся в конфликте друг с другом. Основной сложностью решения таких задач является то, что критерии, как правило, противоречат друг другу.

В общем виде многокритериальная задача оптимизации включает набор N параметров (переменных) и множество K целевых функций. Целевые функции являются функциями многих переменных. Таким образом, при решении многокритериальной задачи необходимо найти оптимум по K критериям, а сама задача формально записывается следующим образом:

где x = (x₁, x₂ ,..., x_N ) ∈ X –     вектор     решений, y = ( y₁, y₂ ,..., y_K ) ∈Y – вектор целевых функций. При этом X обозначает пространство решений, а Y – пространство целей или критериальное пространство.

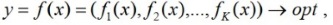
Существует несколько методов решения таких задач генетическими алгоритмами [2]. В данной работе рассмотрены два метода: SPEA (Strength Pareto Evolutionary Algorithm) [3] и VEGA (Vector Evaluated Genetic Algorithm) [4].

Метод VEGA относится к категории селекции по переключающимся целевым функциям. Это означает, что селекция производится по пригодности индивидов для каждого из K критериев в отдельности. Тем самым промежуточная популяция заполняется равными порциями индивидов, отобранных по каждому из частных критериев.

Метод SPEA в корне отличается от других методов, так как в нем:

• для назначения индивидам скалярного значения пригодности используется концепция Парето-доминирования;
• индивиды, недоминируемые относительно других членов популяции, хранятся внешне в специальном внешнем множестве;
• для уменьшения количества индивидов, хранящихся во внешнем множестве, выполняется кластеризация, что в свою очередь никак не влияет на приобретенные в процессе поиска свойства индивидов.

Уникальность и преимущества метода SPEA заключаются в том, что:

– пригодность каждого индивида популяции в данном методе определяется только относительно индивидов внешнего множества, независимо от того, доминируют ли индивиды популяции друг друга;

– несмотря на то, что лучшие индивиды, полученные в предыдущих поколениях, хранятся отдельно – во внешнем множестве, все они принимают участие в селекции;

– для предотвращения преждевременной сходимости, в методе SPEA используется особый механизм образования ниш, где деление общей пригодности осуществляется не в смысле расстояния между индивидами, а на основе Парето-доминирования.

После разработки и реализации алгоритмов, правильность их работы была проверена на тестовых примерах, в которых критерии целевой функции противоречат друг другу:

1. f₁ (x, y) = (x − 6)² + ( y − 4)² → min,

   f₂ (x, y) = (x + 2)² + ( y − 5)² → min

   f₁ (x, y) = (x − 6)² + ( y − 4)² → min,

2. f₂ (x, y) = (x + 2)² + ( y − 5)² → min,

   f₃ (x, y) = (x − 4)² + ( y + 4)² → min,

   f₁ (x, y) = (x −1)² + ( y +1)² → min,

3. f₂ (x, y) = (x + 2)² + ( y − 2)² → min,

   f ₃ (x, y) = (x − 3)² + ( y − 4)² → min,

   f ₄ (x, y) = (x − 4)² + ( y − 2)² → min.

Так как алгоритмы являются стохастическими процедурами, тестирование их заключалось в многократном прогоне на этих тестовых задачах и последующем усреднении результатов. Основной проблемой при нахождении решения является правильная настройка генетического алгоритма, так как при различных параметрах одна и та же задача может иметь противоположные решения. В результате тестирования выяснилось, что алгоритм SPEA показал более точное решение относительно VEGA, однако VEGA более простой в реализации и менее ресурсоемкий.