УДК 519.8

Большое число практических задач поддержки принятия решений в различных областях науки и техники сводятся к решению задачи выбора на множестве альтернатив. Такие задачи возникают на всех этапах поддержки принятия решений: при построении аналитических моделей (выбор структуры и параметров модели), генерировании множества допустимых альтернатив, непосредственно при выборе наилучшей альтернативы в соответствии с некоторыми критериями. В реальных задачах число критериев, по которым оцениваются альтернативы, почти всегда больше одного.

Формально задача выбора сводится к задаче параметрической оптимизации некоторого функционала, где независимые переменные определяют альтернативы, а значение функционала – оценку качества выбора [1]. В случае с единственным критерием существует возможность нахождения наилучшего решения, обеспечивающего экстремум функционала. В случае многих критериев объективного решения не существует, так как необходимо обеспечить компромисс между конфликтующими критериями, а лицо, принимающее решение (ЛПР), должно осуществить субъективный выбор [2]. На практике исследователи часто упрощают многокритериальную задачу выбора до однокритериальной путем определения важности и свертки критериев. Не трудно понять, что компромисса можно достичь разными способами, а потому нет гарантии, что единственное решение по свертке будет приемлемо для ЛПР. Математически множество эффективных решений многокритериальных задач выбора определяется через понятие оптимальности по Парето [3]. Именно из множества Парето должен осуществляться финальный субъективный выбор, так как любое решение вне множества Парето является менее предпочтительным с математической точки зрения. При этом чем точнее и равномернее локализовано (аппроксимировано) множество Парето, тем эффективнее решена формальная задача многокритериальной оптимизации.

Практические задачи оптимизации обладают такими свойствами, как алгоритмическое задание функций, многоэкстремальность, сложная конфигурация допустимой области, наличие нескольких типов переменных, множества постоянства и т. д. Подобные задачи почти не решаются традиционными методами оптимизации. Проблема усугубляется необходимостью учета требования равномерности покрытия множества Парето. Наиболее перспективным подходом к решению подобных задач являются методы интеллектуальных информационных технологий, к которым, в частности, относятся генетические алгоритмы (ГА) [4– 6].

Идея коэволюционного многокритериального генетического алгоритма.

В последние годы предложено множество различных генетических алгоритмов, показавших высокую эффективность при решении многих сложных задач оптимизации. Для решения задач многокритериальной оптимизации наибольшее признание в мировом научном сообществе получили следующие алгоритмы: VEGA (Vector Evaluated Genetic Algorithm) [7], FFGA (Fonseca and Fleming’s MultiObjective Genetic Algorithm) (иногда встречается под названием MOGA (MultiObjective Genetic Algorithm) [8], NPGA (Niched Pareto genetic algorithm) [9], NSGA2 (NonDominated Sorting Genetic Algorithm) [9], SPEA (Strength Pareto Evolutionary Algorithm) [10].

Каждый из алгоритмов обладает своими преимуществами и недостатками. В частности, алгоритмы VEGA и FFGA обладают лучшей сходимостью, но не имеют механизмов обеспечения равномерности покрытия множества Парето, алгоритмы NPGA, NSGA и SPEA обеспечивают хорошее покрытие, но требуют больше вычислительных затрат, а механизмы поддержания разнообразия решений часто выкидывают решения за пределы области Парето. В целом большинство исследователей отмечают алгоритм SPEA как наиболее универсальный [11].

Процесс настройки и контроля параметров конкретного ГА существенно влияет на эффективность решения задачи. Однако этот процесс слабо формализован и часто зависит от опыта и интуиции исследователя. В последние годы наблюдается развитие эволюционных подходов, способных к самонастройке параметров. Одним из подходов к построению самоорганизующихся (самонастраивающихся) процедур является использование коэволюционного подхода [11; 12].

Большинство работ, связанных с построением коэволюционных схем для многокритериальных ГА, используют схему кооперативной коэволюции [13–15]. Цель подобных алгоритмов – провести декомпозицию исходной задачи по переменным, по критериям, по функциональному назначению популяций и т. д. Оценка пригодности индивидов частного алгоритма (подзадачи) происходит с учетом оценок других индивидов. Подобные схемы коэволюционных ГА демонстрируют весьма высокие результаты, но требуют тщательной настройки как параметров частных алгоритмов, так и схем декомпозиции задачи и кооперации.

При использовании схемы конкурирующей коэволюции различные алгоритмы (популяции) развиваются параллельно и независимо в течение некоторого периода. После происходит оценка их эффективности, вычислительные ресурсы перераспределяются от менее эффективных (на данном временном интервале) в пользу более эффективных. Также присутствуют элементы кооперативной коэволюции, в частности, миграция лучших индивидов. Таким образом, при использовании конкурирующей коэволюции нет необходимости определять наилучший для данной задачи (класса задач) алгоритм или его настройки – выбор алгоритма (настроек) осуществляется автоматически в ходе работы.

Очевидно, что использование коэволюционой схемы при решении многокритериальных задач позволит решить проблему конфигурирования алгоритма под задачу. А поскольку различные алгоритмы обладают принципиально различными свойствами, то их совместная работа должна усилить использование индивидуальных сильных сторон и уменьшить влияние слабых. В предложенном подходе в ходе работы поискового алгоритма кроме адаптации численных параметров алгоритма (адаптация алгоритма), но и происходит выбор конкретной конфигурации алгоритма, эффективной на текущем этапе поиска. Такой подход можно назвать самоконфигурируемым многокритериальным ГА.

Авторы назвали такой алгоритм самоконфигурируемым многокритериальным генетическим алгоритмом SelfCOMOGA (Selfconfiguring Coevolutionary MultiObjective Genetic Algorithm).

Общая схема коэволюционного алгоритма SelfCOMOGA.

Схема имеет следующий вид:

Этап 1. Задание множества алгоритмов, участвующих в коэволюции.

Этап 2. Параллельная работа алгоритмов в течение заданного времени – периода адаптации.

Этап 3. Оценка эффективности индивидуальных алгоритмов в адаптационном периоде.

Этап 4. Перераспределение ресурсов и переход к очередному адаптационному периоду – на этап 2.

Рассмотрим эти этапы подробнее.

На первом этапе определяется множество конфигураций алгоритмов, включенных в коэволюцию. Можно выделить как минимум три стратегии:

• детерминированный выбор алгоритмов, свойства которых априори известны и могут быть использованы для решения задачи;
• включение всех возможных комбинаций алгоритмов и их параметров;
• случайный выбор некоторого числа алгоритмов из множества всех возможных комбинаций алгоритмов и их параметров.

Первая стратегия требует привлечения знаний об алгоритмах и решаемой задаче, что не применимо для сложных задач, и противоречит идее самонастройки ГА. Вторая стратегия – весьма затратна, так как число комбинаций может быть большим (сотни вариантов). Третья стратегия, как показывают численные эксперименты, обеспечивает приемлемую эффективность в среднем и при этом нет необходимости привлекать дополнительные сведения об алгоритмах и их свойствах на задаче (классе задач), а значит, этот вариант лучше всего обеспечивает концепцию самонастройки ГА.

Период адаптации является настраиваемым параметром. Эксперименты показали, что значение этого параметра индивидуально для каждой задачи и зависит от критериев, по которым оцениваются алгоритмы. Например, увеличение параметра дает улучшение по критерию расстояния до множества Парето, но ухудшает показатели покрытия множества Парето и наоборот. Более того, значение параметра определяется ограничением числа вычислений целевых функций (вычислительным ресурсом). Можно отметить, что при достаточном вычислительном ресурсе алгоритм в среднем малочувствителен к данному параметру. Тем не менее, данный вопрос необходимо дальнейшем исследовать отдельно.

Ключевым моментом любой коэволюционной схемы является оценка эффективности индивидуальных алгоритмов. Поскольку эффективность оценивается по Парето, то нет возможности прямого сравнения алгоритмов и известные подходы не могут быть использованы. В различных работах предлагаются следующие основные критерии: близость найденного множества решений к истинному множеству Парето и равномерность распределения найденных решений. Очевидно, что для практических задач первый критерий теряет смысл, так как множество Парето неизвестно. Поэтому в данной статье для оценки индивидуальных алгоритмов, включенных в SelfCOMOGA, используются следующие критерии, объединенные в две группы.

Первая группа – статические критерии (оценка по результатам только текущего периода адаптации) – включает в себя два критерия:

• процент недоминируемых решений. Для вычисления создается общий пул решений из решений частных алгоритмов и проводится недоминируемая сортировка [8], а затем определяется, какому алгоритму принадлежат недоминируемые решения;
• равномерность распределения (разброс) недоминируемых решений. Для вычисления используется среднее значение дисперсии расстояний между индивидами по координатам (для множества Парето) или по критериям (для фронта Парето).

Вторая группа – динамические критерии (оценка в сравнении с результатами предыдущих периодов адаптации) – включает в себя еще один критерий – улучшение недоминируемых решений. Для вычисления необходимо сравнить недоминируемые решения алгоритма на прошлом и текущем периоде адаптации. Если текущие недоминируемые решения доминируют прошлые недоминируемые, то произошло улучшение решения задачи, даже если процент недоминируемых решений уменьшился.

Последний этап – этап перераспределения ресурсов. Для этого определяются новые размеры популяций. Все алгоритмы отдают алгоритмупобедителю некоторый процент от своих размеров популяции. При этом каждый алгоритм имеет минимальный гарантированный ресурс, который не распределяется.

В известных коэволюционных схемах каждый новый этап адаптации начинается с одинаковых стартовых точек и используется правило лучший вытесняет худшего. Для многокритериального алгоритма данный подход не пригоден изза требования обеспечения разнообразия Паретооптимальных решений. А поскольку лучшие решения обеспечивают сходимость к множеству Парето, то для перераспределения ресурсов используется схема вероятностного отбора замещение по ранговой селекции: решения с высоким рангом после недоминируемой сортировки имеют большую вероятность быть переданными лучшим алгоритмам, с уменьшением ранга вероятность отбора линейно падает, но шанс быть отобранным остается у всех решений.

Критерии останова коэволюционного алгоритма аналогичны критериям стандартных ГА: ограничение на вычислительный ресурс, отсутствие улучшений (стагнация) и др.

Тестовые задачи и численные эксперименты.

Авторами было проведено исследование эффективности алгоритма SelfCOMOGA на 19 тестовых функциях, которые условно можно объединить в две группы:

• функции 1–6 представляют собой различные тестовые задачи двух переменных. Критерии включают в себя как простые квадратичные функции, так и сложные – (Растригина, Розенброка). Число критериев – от двух до четырех. Данные функции удобны тем, что помимо численных оценок с их помощью можно визуализировать множества и фронт Парето;
• функции 7–19 приняты международным сообществом специалистов по оптимизации на конференции CEC (2009) в качестве сложных задач и рекомендованы для оценки многокритериальных ГА [16]. Это функции FON, POL, KUR, ZDT14, ZDT6, F2, F5, F8, UP4, UP7.

Некоторые результаты тестирования алгоритмов приведены в табл. 1 и 2. Тестирование алгоритма проводилось при следующих условиях. В коэволюцию включены пять различных алгоритмов VEGA, FFGA, NPGA, NSGAII и SPEA, параметры которых выбирались случайно из множества:

Тип скрещивания: одноточечное, двухточечное, равномерное.

Вероятность мутации: высокая, средняя, низкая. Максимальный размер множества Парето (для SPEA): 30, 50, 70.

Радиус ниши (для FFGA и NPGA): 1, 3, 5.

Размер множества сравнения (для NPGA): 3, 5, 7.

Также в таблицах представлены результаты индивидуальной работы базовых алгоритмов, для которых приведены оценки при лучших параметрах, найденных при индивидуальном тестировании.

На каждой задаче для оценки эффективности проводилось 100 независимых запусков алгоритмов. Частные результаты усреднялись. Статистика обрабатывалась с помощью метода дисперсионного анализа – метода непараметрической оценки Манна–Уитни. Различия результатов, представленных в табл. 1, статистически значимы.

В качестве критериев для сравнения эффективности работы алгоритмов выбраны следующие два набора метрик:

Для задач с аналитически заданным множеством и фронтом Парето (F2, F5, F8, UP4, UP7) использовались общепринятые метрики: Generational Distance (GD), Maximum Spread (MS), Spacing (S).

Критерий GD характеризует различие между найденным (PF) и истинным (PF^*) фронтом Парето:

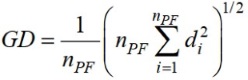
где n_PF = |PF|; d_i – евклидово расстояние (в пространстве критериев) между iм членом PF и ближайшим членом PF^*. В идеальном случае GD = 0.

Критерий MS – характеризует то, насколько хорошо PF^* покрыто PF, большие значения MS показывают, что большая часть PF^* покрыта PF:

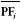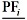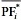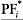где и - максимальное и минимальное значение i-й целевой функции в PF; и – максимальное и минимальное значения iй целевой функции в PF^*; M – количество целевых функций.

Критерий S – характеризует равномерность распределения недоминируемых решений по фронту Парето:

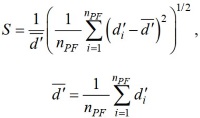
где n_PF = |PF|, d_i – Евклидово расстояние (в пространстве критериев) между iм членом PF и ближайшим членом PF^*.

Для остальных задач сравнение алгоритмов проводилось относительно друг друга на основе недоминируемой сортировки. Для вычисления значений по критериям решения всех исследуемых алгоритмов объединились в общий пул и проводилась недоминируемая сортировка.

Критерий минимального ранга алгоритма K1 – наименьший ранг, который имеет алгоритм после недоминируемой сортировки в общем пуле.

Критерий доли решения с минимальным рангом K2 – процент популяции, имеющий ранг, определённый критерием K1.

Критерий разброса решений с минимальным рангом K3 – дисперсия расстояний в пространстве критериев для решений, имеющий ранг, определённый критерием K1.

Таблица 1. Оценки эффективности алгоритмов на задачах, для которых неизвестны аналитические выражения множества и фронта Парето (набор метрик 1)

Задача	Критерий	SPEA	VEGA	FFGA	NPGA	NSGAII	Self COMOGA	MEAN
F2 (Schaffer’s function)	GD	0,849	1,468	3,334	1,699	0,263	0,460	1,522
	MS	0,750	0,768	2,928	0,730	0,850	0,832	1,205
	S	1,289	0,446	0,096	0,400	0,525	1,483	0,551
UP4	GD	0,421	0,441	0,616	0,616	0,426	0,266	0,504
	MS	0,928	0,933	1,127	0,905	0,928	0,973	0,964
	S	0,368	0,612	0,218	0,279	0,340	0,464	0,363
UP7	GD	1,149	1,881	4,683	2,274	0,305	0,629	2,058
	MS	0,719	0,757	1,571	0,713	0,785	0,792	0,909
	S	1,459	0,444	0,092	0,358	0,556	1,735	0,582

Таблица 2. Оценки эффективности алгоритмов на задачах, для которых неизвестны аналитические выражения множества и фронта Парето (набор метрик 2)

Задача	Критерий	SPEA	VEGA	FFGA	NPGA	NSGAII	Self	MEAN
F2(Schaffer’s function)	K1	2	1	26	2	1	1	7
	K2	0,349	0,357	0,610	0,365	0,424	0,330	0,421
	K3	0,000002	0,000002	0,143085	0,000002	0,000001	0,000001	0,029
4 квадратичные функции	K1	1	1	48	2	1	1	11
	K2	0,208	0,158	0,813	0,147	0,277	0,273	0,321
	K3	0,000005	0,000006	0,407079	0,000013	0,000005	0,000005	0,081422
FON	K1	1	1	27	1	1	1	6
	K2	0,196	0,084	0,631	0,087	0,330	0,353	0,266
	K3	0,455	0,504	1,002	0,547	0,394	0,374	0,580
POL	K1	1	1	10	1	1	1	3
	K2	0,228	0,083	0,214	0,062	0,344	0,316	0,186
	K3	0,198	0,202	0,324	0,125	0,133	0,169	0,196
KUR	K1	1	1	21	2	1	1	5
	K2	0,190	0,158	0,620	0,101	0,344	0,358	0,283
	K3	0,691	0,699	0,395	0,676	0,743	0,741	0,641
ZDT1	K1	3	9	26	10	2	1	10
	K2	0,158	0,115	0,318	0,297	0,578	0,993	0,293
	K3	0,239	0,521	0,758	0,455	0,206	0,159	0,436
ZDT6	K1	4	21	48	12	1	1	17
	K2	0,210	0,235	0,627	0,230	0,162	0,948	0,293
	K3	0,458	0,703	1,100	0,655	0,380	0,311	0,659

В табл. столбец MEAN определяет среднее значение критерия по пяти индивидуальным алгоритмам (для сравнения с результатами алгоритма SelfCOMOGA).

Можно отметить, что на множестве задач эффективность коэволюционного алгоритма в среднем может оказаться хуже лучшего из индивидуальных алгоритмов, но всегда выше средней эффективности по индивидуальным алгоритмам. Поскольку в реальных задачах исследователь не знает заранее, какой алгоритм выбрать и какие настройки использовать, то применение самоконфигурируемого коэволюционного ГА кажется весьма перспективным.

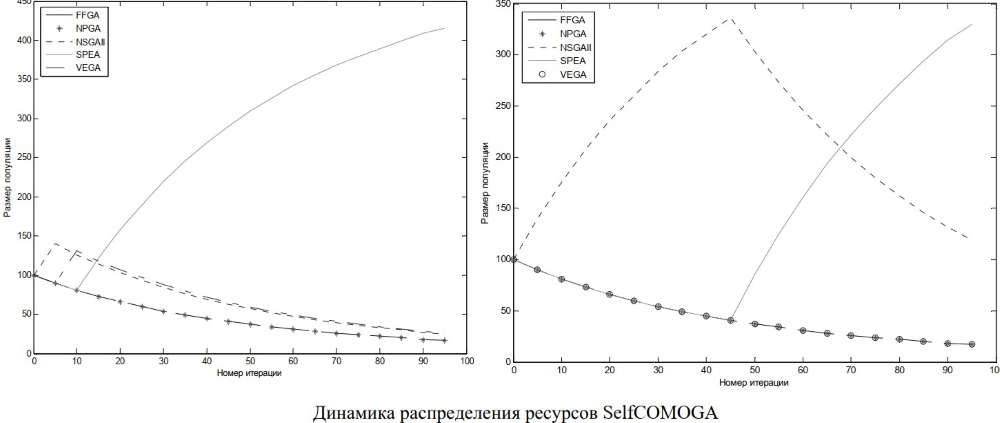
Ниже представлены две примера динамики перераспределения ресурсов: для условно простой задачи (квадратичные критерии) – на рисунке слева – и для сложной – справа.

Как видно из графиков, для простых задач метод SPEA может доминировать на протяжении всего времени работы. Однако эффективность коэволюционного алгоритма в среднем оказывается выше, чем у SPEA отдельно. Более того, в коэволюционном алгоритме параметры SPEA выбираются случайно (не оптимально), а значит несмотря на его победу на всех этапах адаптации, общий эффект достигается за счет совместной работы различных алгоритмов.

Предложенный в данной статье подход позволяет эффективно решать сложные задачи многокритериальной оптимизации, обеспечивая репрезентативную аппроксимацию множества Парето, а использование конкурентной коэволюции позволяет автоматизировать конфигурирование алгоритма под задачу.

Для достаточно простых задач наибольший вклад в коэволюционную динамику вносит алгоритм SPEA, однако эффективность коэволюционного алгоритма в среднем оказывается выше, чем у SPEA самостоятельно, так как при распределении ресурсов все алгоритмы имеют минимальный гарантированный ресурс и дополняют SPEA различными поисковыми стратегиями.

Для более сложных задач преимущества SPEA менее очевидны. В основном этот алгоритм получает больший ресурс на завершающих стадиях, когда требуется поддержка равномерности покрытия множества Парето. На этапе локализации множества Парето ресурс достается алгоритмам, которые с большей скоростью сходятся к паретооптимальным решениям (в частности, алгоритм VEGA).

В дальнейшем авторы планируют расширить область применения предложенного подхода для автоматизирования проектирования интеллектуальных информационных технологий в задачах интеллектуального анализа данных [17], в которых равномерность покрытия множества Парето обеспечивает разнообразие представлений моделей знаний.