Обзор алгоритмов кластеризации, используемых в задачах поиска изображений по содержанию

Поиск изображений по содержанию (CBIR, Content-Based Image Retrieval, в англоязычных источниках также известен как query by image content (QBIC) или content-based visual information retrieval (CBVIR)) [1] является разделом компьютерного зрения и решает задачу поиска изображений на основе анализа присущих ему характеристик. Впервые термин content-based image retrieval был использован Като в 1992 г. для описания проведенного им эксперимента в области автоматического поиска изображений в базе данных на основе особенностей цвета и формы [2]. Данное направление исследований нашло широкое применение в таких областях науки, как медицина, география, безопасность, архитектура, дизайн и пр. [3, 4]. Несмотря на множество работ [5–8], посвященных поиску изображений, данные задачи актуальны и сегодня, за счет возникающих проблем в формализации задачи поиска, разработке методов решения и оценки их качества. Основными проблемами CBIR являются:

• сложность задачи с точки зрения зрительного восприятия человека, т.н. семантический разрыв - человек при сравнении изображений в первую очередь обращает внимание на смысл (семантику), а машина – на заданные характеристики изображения, т.е. различия между представлением изображений в системе и восприятием пользователя; [9];
• необходимость работы с большими объемами данных [10];
• точность получения изображений из БД с использованием сети интернет [2];
• повышение скорости выполнения алгоритмов [5];
• повышение близости искомых образов объекта к эталонному изображению не только по структуре, но и по смысловому содержимому [8].

Алгоритмы поиска изображений по содержанию постоянно совершенствуются, поэтому их периодический обзор является актуальной научной задачей.

Альтернативой CBIR является поиск изображений по ключевым словам и текстовым аннотациям (рис. 1). Таким алгоритмом является DBIR (Description Based Image Retrieval) [11], к плюсам которого можно отнести его применимость при поиске текстов, соответствующих семантике изображения. Сложность использования DBIR заключается в сложности исполнения и субъективном характере составления аннотаций поиска. К плюсам CBIR относят автоматическое построение объективного индекса. К минусам относят наличие семантического разрыва и сложность построения запросов для пользователей.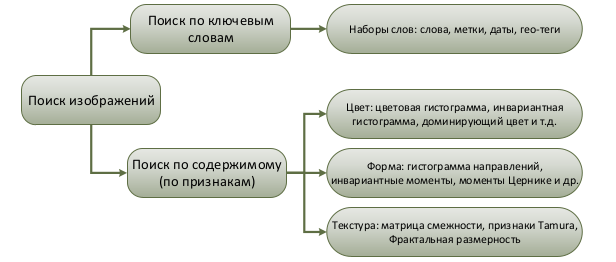

Поиск изображений по содержанию основывается на распознавании анализируемых объектов. Проблема распознавания является весьма общей, хотя она и возникла в связи с решением частных задач – задач распознавания фигур (цифр, букв, изображений), звуков (речи, шума), диагностики заболеваний или неисправностей и т.п. Распознавание представляет первую и важную ступень обработки информации, получаемой нами при помощи органов чувств и приборов. Распознавание образов – это отнесение исходных данных к определенному классу путем выделения существенных признаков или свойств, характеризующих эти данные (из общей массы несущественных деталей). Под классом образов понимается некоторое подмножество, определяемое рядом свойств, общих для всех элементов этого класса. То общее, что объединяет объекты в класс, называют эталоном. Например, на рис. 2 находится принятое за эталон изображение для поиска автобуса, где линиями справа показаны зоны поиска.

В качестве эталона выбирают образ, обладающий минимальной изменчивостью значений признаков на множестве возможных представлений данного образа. Предполагается, что образу (эталону) соответствует компактное множество точек в пространстве признаков (гипотеза компактности), образующих разделимые классы. Однако шумы, помехи (организованные и неорганизованные), структурные вариации одного и того же представителя класса приводят к значительному увеличению указанного объёма и, как следствие, перекрытию классов, а значит, к снижению достоверности классификации [12]. При поиске по содержанию каждое изображение коллекции описывается в системе векторами признаков (feature vector) (или просто признаками) - наборами числовых параметров, отражающих свойства низкоуровневых характеристик изображения. Вектора признаков принимают значения в пространстве признаков. Задав метрику на таком пространстве, можно сравнивать изображения друг с другом, вычисляя расстояние между соответствующими им векторами. Алгоритмы построения векторов признаков являются ядром любой системы поиска по содержанию. От выбора признаков и метрик для их сравнения зависит качество поиска [5]. При запросе искомого вектора признаков поиск идет до совпадения с хранящимися векторами признаков в БД, что замедляет работу при наличии большого объема хранимых изображений.

Для повышения скорости выполнения запросов и получения оптимального результата используется кластерные алгоритмы для поиска изображений по содержанию. Определение кластеризация данных (data clustering) впервые был применен в публикации 1954 года, посвящённой обработке антропологических данных [14]. Термин кластеризация данных имеет такие синонимы: типизация, стратификация, группировка, таксономия, классификация с самообучением и пр. [15]. Кластеры изображений формируются на основе признаков, извлеченных из изображений:

• По признакам цвета. В этом способе из изображения извлекается цвет, который далее рассматривается как вектор признака. Признак цвета может быть извлечен множеством способов, таких как Histogram, Color moments, Color Correlogram, color coherence vector и др [13]..
• По признакам текстуры. В этом способе за вектор признака принимается текстура изображения [16-18].
• По признакам формы. В этом способе форма (ее границы) используются как вектор признаков. Robert, Sobel, Prewitt, Kirsch, Robinson, Marr-Hildreth, LoG и Canny – виды методов выделения границ, использующегося для создания вектора признаков [19–26].

Рассмотрим более подробно следующие алгоритмы: K-средних, нечеткая кластеризация, биоинспирированные алгоритмы.

Метод k-средних

Самым популярным среди статистических считается метод кластеризации k-средних (k-means) [27–29], состоящий следующих этапов.

Изображение сегментируется на блоки заданного размера (чаще всего квадратные). Для каждого блока происходит вычисление средней цветовой характеристики. Блоки изображения случайным образом распределяются на n кластеров, при этом начальное значение количества кластеров принимается равным двум.

Производится расчет центра для каждой из характеристик каждого кластера по формуле 1.

(1)

R_j – количество точек j-го кластер, X_i – значения характеристик блоков, входящих в кластер

Вычисление расстояния у каждого блока до центра (формула 2) каждого из кластеров – перегруппировка блоков внутри кластеров, т.е. соотнесение блока к тому из кластеров, для которого расстояние по всем характеристикам минимальное.

(2)

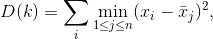
Пересчет центров кластеров каждый раз после включения нового блока в кластер.

Инкремент n и повтор п.1-4 до тех пор, пока:

диапазон значений D(n) внутри каждого из кластеров не станет меньшим некоторого экспериментально подобранного числа K;

увеличение количества кластеров перестает значительно менять результат группировки: D(n)-D(n-1) < K;

n выходит за пределы экспериментально установленного числа [27, 28] кластеров.

Базовый кластерный алгоритм k-средних является очень чувствительным к начальной кластеризации, выбросам и шуму [30, 31], зависим от начальных условий, что существенно снижает его применимость в чистом виде для решения задач поиска изображений по содержанию.

Нечеткая кластеризация

Одним из направлений модификации k-means алгоритма являются методы fuzzy- или нечеткой кластеризации. Их авторы [32, 33] принимают изображение в виде нечетких множеств и используют функции принадлежности, на основании которых происходит определение по кластерам блоков изображения. Нечеткая кластеризация позволяет разделить вектор признаков между несколькими кластерами, что соответствует смешанным векторам признаков, существующим при наличии посторонних данных на изображении, аналогичном искомому. Вектор измерений каждого из кластеров может принадлежать всем кластерам с коэффициентом принадлежности u_ij ∈ [0;1] , определяющим степень принадлежности j-го вектора i-му кластеру, формулы 3, 4:

(3)

(4)

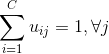
где С – число кластеров, L – количество векторов признаков.

Значения функции уровней принадлежности, принимают значение от 0 до 1, где близость к 1 означает высокую степень сходства вектора с кластером. Далее, в зависимости от поставленной задачи, возможно применение методов C-средних (Fuzzy C-means, FCM) [34, 37] или кластеризации с регуляризацией (Possibilistic C-means, PCM). Основным отличием FCM от PCM является снятие ограничения на элементы матрицы принадлежности по кластерам. В алгоритме PCM членство вектора в кластере является относительным, а в FCM – абсолютным, независящим от значений членства этого вектора в других кластерах. Для выполнения алгоритма PCM на некотором наборе данных является предварительное выполнение алгоритма FCM на этом же наборе [35]. Основная работа данных алгоритмов заключается в итерационном перестроении матрицы уровней принадлежности векторов признаков некоторым кластерам и перерасчете центров кластеров. Условия окончания действия алгоритмов:

выполнение заданного числа итераций;

достижение состояния стабильности, увеличение количества кластеров перестает значительно менять результат группировки: D(n)-D(n-1) < K.

Данные алгоритмы в чистом виде требуют больших временных затрат, что обуславливает разработку комбинированных или новых методов.

Реализация нечетких запросов к базам данных при помощи лингвистических переменных рассмотрена в [41, 42].

Биоинспирированные алгоритмы

Более удобными в применении являются биоинспирированные алгоритмы [40]. Рассмотрим комбинированный алгоритм муравьиной колонии и метода роя частиц (ACPSO) для кластеризации изображений в задаче CBIR. Пусть в некоторой системе цветные и обработанные изображения хранятся в базе данных. Вектор характеристик генерируется на основе признаков формы и хранится в базе данных. Используя алгоритм кластеризации, изображения группируются и создаются кластеры. Введенное изображение для поиска передается в качестве входных данных, и в зависимости от сходства ему назначается наиближайший кластер. На рис. 3 отображены основные этапы данного подхода [36].

На этапе получения признаков используется метод выделения границ Собеля. Начальный градиент изображения вычисляется по осям X и Y, величина градиента – по формуле (5). Полученный градиент представляется как коэффициент мощности, затем на его основе формируется вектор признаков. Сокращенный набор вектора признаков представляет собой матрицу изображения.

(5)

где G_x – градиент изображения по оси X, G_y – градиент по оси Y, G – величина градиента изображения.

После получения все векторы признаков сохраняются в базе данных. Затем для группировки изображений применяется алгоритм ACPSO. Муравьиный алгоритм применяется для инициализации центроида кластера, а метод роя частиц – для поиска квазиоптимума кластеризации.

При помощи CBIR извлекаются характерные особенности (признаки изображений). Набор данных передается на вход в алгоритм ACO, распределяются случайным образом в двухмерную сетку. Сначала все части данных, которые были извлечены с помощью техники выделения границ, передаются через двухмерное пространство в сетке. Каждый муравей случайным образом движется по сетке, подбирая и отбрасывая части данных, Решение подобрать или бросить данные случайно, но зависит от того, являются ли части данных ближайшими соседями муравья. Вероятность отброса данных увеличивается, если муравьи окружены схожими данными по соседству. И наоборот, вероятность подбора данных увеличивается, если данные окружены непохожими данными или когда нет данных по соседству, чтобы собрать центроид кластера, муравьи распределяются случайным образом. С каждым новым шагом позиция муравья изменяется.

Основанная на вычислении каждая муравьиная позиция упрощена для каждого повтора, который будет давать новый результат до тех пора, пока не будет достигнуто n повторений. Последняя итерация дает набор центроида, который передается в PSO алгоритм.

Начальный набор центроидов, полученный из ACO алгоритма, является p решением, т.е хорошим с точки зрения оценки стоимости. Оно задается как первая популяция частиц для PSO кластеризации. Здесь, каждое решение (частица) это набор центроидов входных данных. Следовательно, объем популяции PSO кластеризации это p X (k*d) матрица и стоимость скорости установлена в ноль. Затем, для каждого результата, пригодность вычисляется, основываясь на многоцелевой функции, то есть задача минимизации или максимизации для корректной кластеризации.

Заключение

В процессе анализа установлено что основными проблемами CBIR являются: сложность задачи с точки зрения различия между представлением изображений в системе и восприятием пользователя, необходимость работы с большими объемами данных. Перспективными направлениями развития CBIR является: повышение точности получения изображений из БД с использованием сети интернет, повышение скорости выполнения алгоритмов, увеличение степени близости искомых образов объекта и эталонного изображению не только по структуре, но и по смысловому содержимому.

По причине сложности проблем реализации CBIR алгоритмы поиска изображений по содержанию постоянно совершенствуются в том числе дополняются новыми математическими и алгоритмическими инструментами такими как: нечеткая логика, биоинспирированные алгоритмы и т.д.

В статье были перечислены извлекаемые из изображений признаки, по которым формируются кластеры изображений. Указаны способы извлечения данных признаков и рассмотрены следующие алгоритмы: статистический метод кластеризации k-средних, нечеткая (fuzzy) кластеризация, комбинированный алгоритм муравьиной колонии и метода роя частиц (ACPSO).

Благодарность

Работа выполнена при финансовой поддержке грантов РФФИ No 15-01-05129-а, No 16-01-00390-а и No 16-01-00391-а.

Литература

1. Manning, C.D., Raghavan, P., Schütze, H. Introduction to Information Retrieval. Cambridge, UK:Cambridge University Press. 2008. P.496.
2. A Sketch Retrieval Method for Full Color Image Database. Kato, T., Kurita, T., Otsu, N., Hirata, K. Query by Visual Example, Proc. of Int. Conf. on Pattern Recognition, 1992. pp. 530-533.
3. Image retrieval: Ideas, influences, and trends of the new age. R. Datta, D. Joshi, J. Li, and J. Z.Wang. ACM Computing Surveys (CSUR). Vol. 40. No. 2. 2008. — P.2.
4. Kondekar, V. H., Kolkure, V. S., Kore, S.N. Image Retrieval Techniques based on Image Features: A State of Art approach for CBIR. (IJCSIS) International Journal of Computer Science and Information Security, Vol. 7. No. 1. 2010. p.7.
5. Васильева, Н. С. Построение и комбинирование признаков в задаче поиска изображений по содержанию: дис. ... канд тех. наук: 05.13.11. - СПб., 2010. C.164.
6. Левашкина, А.О. Разработка методов поиска изображений на основе вычислительных моделей визуального внимания: автореф. дис. ... канд. тех. наук: 05.13.17. Новосибирск, 2009. C.24.
7. Пименов, В.Ю. Метод распознавания сверхбольших выборок изображений: дис. ... канд. физ.-мат. наук: 05.13.01. СПб., 2010. C. 110.
8. Лыонг Хак Динь. Аналитические и процедурные модели для информационной системы распознавания графических объектов в условиях неопределенности: дис. ... канд. тех. наук: 05.25.05. Тамбов, 2014. c. 120.
9. Мельниченко, А., Гончаров А. Методы поиска изображений по визуальному подобию идетекции нечётких дубликатов изображений. Труды РОМИП 2009. – СПб.:НУ ЦСИ. 2009. С. 108-121.
10. Гулаков, В. К., Трубаков А.О. Проблема большого объема векторов характеристик в задаче многомерного индексирования графической информации. Известия Волгоградского государственного технического университета. Волгоград, 2010. No 11. С. 133-137.
11. Anna Saro Vijendran, S. Vinod Kumar. A New Content Based Image Retrieval System by HOG of Wavelet Sub Bands. International Journal of Signal Processing, Image Processing and Pattern Recognition Vol. 8, No. 4 (2015), pp. 297-306
12. Десятников, И.Е. Поиск изображений по визуальному подобию в сети Интернет. Материалы Международной научно-технической конференции Информационные системы и технологии (ИСТ-2013), 19 апреля 2013 г. Н. Новгород: НГТУ, 2013. С. 240-241.
13. Roy K., Mukherjee J. Image Similarity Measure using Color Histogram, Color Coherence Vector, and Sobel Method. Acm Computing Surveys, International Journal of Science and Research (IJSR). 2013. Vol 2. pp. 2319-7064.
14. Jain, A.K. Data clustering: 50 years beyond K-means. A.K. Jain. Patt. Recogn. Lett. 2010. Vol. 31. Is. 8. pp. 651–666.
15. Айвазян С. А., Бухштабер В. М., Енюков И. С., Мешалкин Л. Д. Прикладная статистика: классификация и снижение размерности. М: Финансы и статистика, 1989. C. 607.
16. Coggins J.M. A Framework for Texture Analysis Based on Spatial Filtering Ph. D. Computer Science Department. Michgan: Michigan State University, 1982. P.168.
17. Tamura, H., Mori, S., Yamawaki, Y. Textural Features Corresponding to Visual Perseption. IEEE Transactions on Systems, Man and Cybernetics. 1978. No 8. pp. 460-473.
18. Haralick, R.M. Statistical and Structural Approaches to Texture. Proc. of the IEEE. 1979. Vol. 67. pp. 786-804
19. Робертс, Л. Автоматическое восприятие трехмерных объектов. Интегральные роботы: сб. Вып. 1. под ред. Г.Е. Поздняка. М.: Мир, 1973. с.162-208.
20. Sobel, I.E. Camera Models and Machine Perception. Ph.D. Thesis. Palo Alto, Calif., Stanford University. 1970. P.60.
21. Prewitt, J. M. S., Object Enhancement and Extraction. Eds. B. S., Lipkin, A., Rosenfeld. Picture Processing and Psychopictorics Academic Press, New York. 1970. pp.75-149.
22. Kirsch, R. Computer Determination of the Constituent Structure of Biological Images. Computers and Biomedical Research. 1971. Vol. 4. pp. 315- 328.
23. Robinson, G. S., Color Edge Detection. Proceeding SPIE Symposium on Advances in Image Transmission Techniques. San Diego, California. 1976. Vol. 87. pp. 126-133.
24. Marr, D., Hildreth, E. Theory of Edge Detection. Proceedings of the Royal Society of London. Series B, Biological Sciences. 1980. Vol. 207. No. 1167. pp. 187–217.
25. Canny, J. F. A computational approach to edge detection. IEEE Trans. Pattern Anal. Machine Intell. 1986. Vol. PAMI-8. No. 6. pp. 679-697.
26. Argyle, E. Techniques for edge detection. Proc. IEEE. 1971. Vol. 59. pp. 285-286.
27. Wang, J. Z., Li, J., Wiederhold, G. SIMPLIcity: Semantics-Sensitive Integrated Matching for Picture Libraries. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2001. Vol. 23. No. 9. pp. 947-963.
28. Wang, J. Z., Du, Y. Scalable Integrated Region-based Image Retrieval using IRM and Statistical Clustering. Proc. ACM and IEEE Joint Conference on Digital Libraries, Roanoke, VA, ACM. 2001. pp. 268-277.
29. Hartigan, J. A., Wong, M. A. Algorithm AS136: a k-means clustering algorithm. Applied Statistics. 1979. Vol. 28. pp. 100-108.
30. Optimization CBIR using K-Means Clustering for Image Database. Rejito, J., Retantyo Wardoyo, Sri Hartati, Agus Harjoko. International Journal of Computer Science and Information Technologies. . 2012. Vol. 3. pp. 4789-4793.
31. Taher Niknam, Babak Amiri. An efficient hybrid approach based on PSO, ACO and k-means for cluster analysis. Applied Soft Computing, Elsevier. 2010. Vol. 10. pp. 183-197.
32. Baraldi, A., Blonda, P. A Survey of Fuzzy Clustering Algorithms for Pattern Recognition – Part I. IEEE Transactions on systems, man, and cybernetics – Part B: Cybernetics. 1999. Vol. 29. No. 6. pp. 778-785.
33. Deer, P. Change Detection using Fuzzy Post Classification Comparison: PhD thesis. Department of Computer Science, the University of Adelaide, 1998. p.284.
34. Bezdek J.C. Pattern recognition with fuzzy objective function algorithms. Plenum Press, New York, 1981. pp. 65-95
35. Krishnapuram, R., Keller, J.M. A possibilistic approach to clustering. IEEE Transactionson Fuzzy Systems. 1993. Vol 1. pp. 98 –110.
36. Hybrid Swarm Intelligence Method for Post Clustering Content Based Image Retrieval. Shubhangi, P., Meshrama, Anuradha, D., Thakareb, Santwana Gudadhe. 7th International Conference on Communication, Computing and Virtualization. 2016. pp. 509 – 515
37. James Z. Wang, Jia Li, Gio Wiederhold. SIMPLIcity: Semantics-sensitive Integrated Matching for Picture Libraries. IEEE Trans. on Pattern Analysis and Machine Intelligence. 2001. Vol. 23. No.9. pp. 947-963.
38. Jia Li, James Z. Wang. Automatic linguistic indexing of pictures by a statistical modeling approach. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2003. Vol. 25. No. 9. pp. 1075-1088.
39. Миркин, Б. Г. Методы кластер-анализа для поддержки принятия решений: обзор: препринт WP7/2011/03/ М.: Изд. дом Национального университета Высшая школа экономики, 2011. C. 88.
40. Гладков Л.А., Курейчик В.В., Курейчик В.М., Сороколетов П.В. Биоинспирированные методы оптимизации. М.: Физматлит, 2009. 384 с.
41. Венцов, Н.Н., Долгов, В.В., Подколзина, Л.А. Об одном способе построения запросов к базе данных на основе аппарата нечеткой логики. // Инженерный вестник Дона, 2015, No3 URL: ivdon.ru/ru/magazine/archive/n3y2015/3172
42. Венцов, Н.Н. Разработка алгоритма управления процессом адаптации нечетких проектных метаданных // Инженерный вестник Дона, 2012, No1 URL: ivdon.ru/ru/magazine/archive/n1y2012/630