A Fast Approach for Integrating ORB Descriptors in the Bag of Words Model
Abstract. In this paper we propose to integrate the recently introduces ORB descriptors in the currently favored approach for image classification, that is the Bag of Words model. In particular the problem to be solved is to provide a clustering method able to deal with the binary string nature of the ORB descriptors. We suggest to use a k-means like approach, called k-majority, substituting Euclidean distance with Hamming distance and majority selected vector as the new cluster center. Results combining this new approach with other features are provided over the ImageCLEF 2011 dataset.
Keywords: Image Retrieval, BOW, Color descriptor
1. Introduction
One of the most interesting trends in multimedia retrieval, side by side with the improvement of the representation accuracy of descriptors by quantizing even more efficiently visual information, is the decrease of the computational demands of the algorithms. Improving the retrieval performance while reducing the computational effort demanded to the processing devices is a great engineering challenge. Often this problem is solved by finding approximatded solutions and a performance reduction that guarantee the most significant decrease in processing time. This trend is also highly supported by the variety of multimedia devices which are mainly sold to customers, such smartphones and tablets. These devices in fact have lower computational capabilities, lower memory and the strong constraint of the battery life, therefore require a careful algorithmic design.
This problem is even more significant considering that the current trend in multimedia retrieval is to apply some sort of local description, composed by a region detection and a region description, which is usually computationally demanding. Moreover, they are good candidates for object detection tasks, but if we want to perform similarity retrieval or content classification (therefore creating a global representation of the content itself), we have to employ the bag-of-words model to construct a visual vocabulary. Again, this procedure is computationally very expensive since it requires a clustering step, often k-means.
Considering the ImageCLEF 2011 Photo Annotation dataset (Fig.1) as the reference throughout the manuscript, we can see that the last years best performance has been obtained by University of Amsterdam’s Concept Detection System, [1] combining 3 SIFT with Harris-Laplace corner detector, plus 3 SIFT with dense multiscale sampling every 6 pixels, and a training with SVM using χ2 kernel. Therefore, authors obtained a 24000-dimension feature vector, with a training time of several days on an high end PC. The process is complex even in testing, requiring descriptors extraction, nearest neighbor computation for every word of the vocabulary and the classification with SVM.
In this work, we propose a solution to reduce the computational effort of this entire paradigm, accepting a certain loss of performance but a significant gain in speed. We move towards much more easy to compute features, covering gradient and color information. In particular, we exploited a class-based optimized histogram, the CENTRIST feature expressing an histogram of local binary patterns [2] and ORB [3], a binary local descriptor. For the latter, we propose a novel vocabulary creation technique designed for binary data, by exploiting a majority voting to define the centroid. In the following, we will detail how the combined use of these fast descriptors and some optimizations on the binary nature of the data can lead to impressive processing speedup yet maintaining good classification performance.
2. Lightweight features
The SIFT keypoint detector and descriptor [4], although over a decade old, have proven to be remarkably successful in a number of applications using visual features, including object detection and recognition, image stitching, scene classification, etc. This descriptor has been also extended to color images in the form of RGB-SIFT, Opponent-SIFT and C-SIFT, as described by van de Sande et al. in [5]. However, it requires an intensive computational effort, especially for real-time systems, or for low-power devices such as cellphones. This has led to an increased research for replacements with simpler descriptors with lower computation demands. This trend started with SURF [6], but since then a lot of other descriptors have been proposed in literature, always focusing not only on performance but also on speed: we can refer to VLAD [7], BRIEF [8], DAISY [9] among the most recent proposals. There has also been research aimed at speeding up the computation of SIFT, most notably with GPU devices [10], or the exploitation of approximate nearest neighbor techniques, starting from LSH [11] up to product quantization [12].
Also a great variety of global features has been proposed to tackle the retrieval problem, for example color histograms, GIST [13] and HOG [14]. Usually these features are easier to compute and do not require the quantization step typical of the bag-of-words model which is necessary to create a global representation (an histogram of visual words) from the aforementioned local descriptors.
Here we would like to explore a set of lightweight features, both local and global, in order to define a retrieval strategy able to combine good performance and very low computational demands. We have in mind the straightforward application of such algorithms in mobile devices, but we do not investigate this aspect in this work.
2.1 ORB descriptor
In a recent paper, Rublee et al. [3] propose a very fast binary descriptor based on BRIEF, called ORB, which is rotation invariant and resistant to noise. They demonstrate through experiments how ORB is up to two orders of magnitude faster than SIFT, while performing as well in many situations. The efficiency is tested on several real-world applications, including object detection and patch-tracking on a smart phone. The investigation of variance under orientation was critical in constructing ORB and decorrelating its components, in order to get good performance in nearest-neighbor applications. An interesting aspect is that the authors have also contributed a BSD licensed implementation of ORB to the community, via OpenCV 2.3.
The ORB descriptor (Oriented FAST and Rotated BRIEF) builds on the well-known FAST keypoint detec- tor [15] and the recently-developed BRIEF descriptor [8].
The original FAST proposal implements a set of binary tests over a patch, by varying the intensity threshold between the center pixel and those in a circular ring around the center. The Harris corner measure [16] has been used to provide an evaluation of the corner intensity. In ORB the missing orientation information of FAST are instead complemented with Rosin’s corner intensity [17]. In particular, the moment mpq of a patch Ip can be computed as:
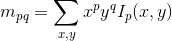
We can further compute the centroid C as:

and by constructing a vector from the patch center O to the centroid C, we can define the relative orientation of the patch as:
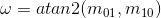
The patch description has been provided starting from the BRIEF operator [8], a bit string representation constructed from a set of binary intensity tests. Given a smoothed image patch Ip of an intensity image I, a binary test τ can be performed as:
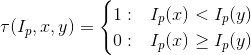
The final feature is defined as a vector of n binary tests:
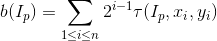
The intra-patch locations for the tests, therefore the choice of the vector
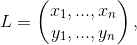
influences the quality of the descriptor itself. A solution could be a grid sampling based set of sets by taking into consideration the patch orientation, so multiplying these locations with the rotation matrix. However, by analyzing the distribution of the tests, this solution brings a loss of variance and increase the correlation among the binary tests (since tests along the edge orientation statistically produce similar outcomes). This heavily impacts the descriptor effectiveness, describing redundancy more than distinctiveness. To solve the problem, the authors 3 employed a learning algorithm, sampling tests from 5 × 5 subwindows of the 31 × 31 patch window chosen for the descriptor, running each test against all training patches. The result is a predefined set of 256 tests called rBRIEF.
2.2 Centrist descriptor
Census Transform (CT) is a non-parametric local transform originally designed for establishing correspondence between local patches [18]. Census transform compares the intensity value of a pixel with its eight neighboring pixels, as illustrated in Eq. 7. If the center pixel is larger than (or equal to) one of its neighbors, a bit 1 is set in the corresponding location. Otherwise a bit 0 is set.

The eight bits generated from intensity comparisons can be put together in any order, but we follow the convention described by Wu et al. [2] and collect bits from left to right, and from top to bottom). This is the Census Transform value (CT value) for this center pixel. Census Transform is robust to illumination changes, gamma variations, etc.
A histogram of CT values for an image or image patch can be easily computed defining the CENTRIST descriptor (CENsus TRansform hISTogram)[2]. Only 16 operations are required to compute the CT value for a center pixel (8 comparisons and 8 additional operations to set bits to 0 or 1). The cost to compute CENTRIST is linear in the number of pixels of the region we are interested in. There is also potential for further acceleration to the computation of CENTRIST, because it mainly involves integer arithmetic that are highly parallel in nature.
2.3 Color histogram descriptor
Working on large datasets for search and classification purposes fixed length signatures are often adopted, being more easily used in different hashing and indexing tasks. Color histograms are a common solution, and using a non uniform division of the color space could better describe the distribution of color aspects in the dataset. Since we aim at exploiting color for visual object classification, we would like to employ a dynamic binning which emphasizes the classes peculiarities. This is different from extracting a set of colors based on the data only (for example by clustering in the color space), but is a task of feature selection by incorporating data classification information in the definition of the color signature.
A color in a color space C is denoted by c. Given an image I, the color distribution for the image is
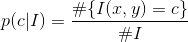
Given a class of images Cj, with j = 1,...,J, described by a training set of images I, we can define pj(c) as the L1-normalized sum of the color distributions of all images in that class. We approach the problem of finding a class optimized binning with a greedy procedure inspired to the median cut algorithm [19].
A box is the set of colors contained within a parallelepiped defined by two extreme colors low (l) and high (h), with l, h ∈ C:
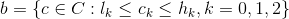
To simplify the equations, from now on we will assume a three channels color space. We will equivalently write b = (l, h). We call mj(b) the mass of box b in class j, such as
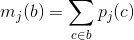
The total mass of b is

We also denote C(b) as the class associated to box b, that is the class with maximum mass for the box:
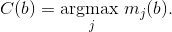
The error induced by considering colors in b to be all of class Cj is defined as:

We define a split of a box as s = (v, k), meaning that we divide the box along channel k at position v. Splitting a box has the purpose of better describing the colors of that box, thus it is reasonable to assume that this will lower the error. We call δ(b, s) the difference between the current error caused by the box b and the one obtained after the splitting s. δ(b) = maxs δ(b, s) is the error induced by the best split. We will then choose to split the box which maximizes its δ.
The algorithm employs a list of boxes, initially containing a single box enclosing the whole 3D color space, described as b0. For example in an 8-bit RGB color space b0 = ((0, 0, 0), (255, 255, 255)). At each iteration step we extract from the list the box which has the maximum delta value, then it is split such as to minimize the sum of the errors after the split. The resulting boxes are put back in the list. The algorithm proceeds until the required number of boxes/histogram bins is obtained. Pseudo code is given in Algorithm 1. A fast technique to perform this computation, namely 3D Integral Histograms, has been proposed by Grana et al [20].
A bag of words model for binary descriptors
While histogram based features are directly ready to be used in image classification or retrieval tasks, local features require an additional quantization step to be transformed into global image features. The classic approach is to employ k-means clustering using Euclidean distance between feature vectors, and this has proved to be effective, even if computationally demanding during the training phase.
Unfortunately when dealing with a vector of binary features, Euclidean distance is not the metric of choice, and the average vector is undefined. A reasonable and effective distance between binary vectors is the Hamming distance (the number of different bits in corresponding positions), but still no average is provided. We could tackle the problem reverting to k-medoids (PAM algorithm), 21 but this would require the computation of a full distance matrix between the elements to be clustered, even worsening the problem. Therefore, to compute the centroid of a set of binary vectors based on the Hamming distance, we have introduce a voting scheme. In particular, corresponding elements of each vector vote for 0 or 1. For determining each element of the centroid, the majority rule is used, with ties broken randomly. We call this variation of the Lloyd algorithm “k-majority algorithm” and we resume it in Algorithm 2.
The algorithm processes a collection of D binary vectors and seeks for a number k of good centroids, that will become the visual dictionary for the Bag-Of-Words model. Initially, these k centroids are determined randomly (line 2). At each iteration, the initial step (lines 4-6) is the assignment of each binary vector to the closest centroid: the current binary vector d is therefore labelled with the index of the closest centroid. This part is essentially shared by many common clustering algorithms. The second step (lines 7-12) is the majority voting used to redefine the vector clustering. For each cluster c, we take into consideration every binary vector d belonging to it. Every bit of an accumulator vector v is increased by 1 if the corresponding bits in d is 1. At the end, the majority rule is used to form the new centroid c′: for each element v i in v, if the majority of vectors voted for 1 as bit value in v i , then c′i takes 1, otherwise c′i takes 0. The algorithm iterates until no centroids are changed during the previous iteration.
A fundamental advantage of the k-majority approach is that both the Hamming distance and the majority voting step can work on the byte packed vector string. In particular the Hamming distance may be implemented leveraging both SSE instructions and specific bitwise hardware instructions. An example optimized version of an Hamming distance function is provided in Fig. 2 (If specialized hardware instructions are not available, it is still possible to employ some smart bitwise operations as
those proposed in http://graphics.stanford.edu/~seander/bithacks.html#CountBitsSetParallel).unsigned HammingDistance (__m128i *x, __m128i *y) {
__m128i xorValue = _mm_xor_si128(*x,*y);
unsigned __int64 *xorValue1 = (unsigned __int64 *)(&xorValue);
return (unsigned)__popcnt64(*xorValue1) + (unsigned)__popcnt64(*(xorValue1+2));
}
By using Hamming distance and majority voting in the cluster assignment step, which has to go through all elements to be clustered, we can obtain a speedup in the order of 100.
4. Experiments
The ImageCLEF 2011 Photo Annotation and Concept-based Retrieval Tasks pose the challenge of an automated annotation of Flickr images with 99 visual concepts and the retrieval of images based on query topics. The participants were provided with a training set of 8,000 images including annotations, EXIF data, and Flickr user tags. The annotation challenge was performed on 10,000 images. In our experiments we focused only on the visual part of the challenge, ignoring the tag based additions, which is known to provide fundamental improvements on the performance, but is outside the scope of this article.
As a reference comparison we selected the University of Amsterdam concept detection system, which is an improved version of the system from the ImageCLEF book [22], where they have performed additional experiments which give insight into the effect of different sampling methods, color descriptors and spatial pyramid levels within the bag-of-words model. Their runs roughly correspond to Harris-Laplace and dense sampling every 6 pixels (multi-scale) with 4-SIFT and Harris-Laplace and dense sampling every pixel (single-scale) with 4-SIFT. However, instead of 4-SIFT, they only consider three ColorSIFT variants in 2011. One of these three is an optimized color descriptor which allows these three to perform as good as 4-SIFT.
We implemented and tested the concept detection system using 3 color SIFT descriptors (namely RGBSift, Opponent Sift and C-Sift) computed with multiscale dense sampling. The descriptors have been quantized with the k-means algorithm and 99 SVMs have been trained with the concatenation of the 3 BoWs descriptors. Parameters of the SVMs have been optimized with 4-fold cross validation and grid search. This was compared with the single features performance and their combination and the results are summarized in Table 1. Results have been evaluated with MiAP (Mean interpolated Average Precision), using the ImageCLEF provided tools.
| Descriptor | MiAP |
|---|---|
| Color Histogram | 0.17 |
| CENTRIST (3 channels) | 0.21 |
| Harris + RGB SHIFT | 0.23 |
| Harris + 3 SHIFT | 0.27 |
| Harris + 3 SHIFT + Hist + CENTRIST | 0.29 |
| Dense + 3 SHIFT + Hist + CENTRIST | 0.30 |
| ORB (3 channels) | 0.21 |
| Dense + ORB | 0.22 |
| Dense + ORB + Hist + CENTRIST | 0.26 |
Looking at the results in Table 1 it is clear that the ORB descriptor is providing much less information, when compared with the SIFT counterpart. Moreover we naively extracted the descriptor separately for the RGB channels, in order to incorporate color information, but this falls way behind the color studies and the optimization available in the color SIFT descriptor. Nevertheless it is interesting to note that the performance are still significant and there is space to improve the descriptor performance.
The main result is instead related to the computational time required by the technique. The color descriptor software available from the ISIS group (www.colordescriptors.com) has this caveat: “Clustering with 250,000 descriptors on 384D (ColorSIFT) descriptors will take at least 12 hours per iteration of k-means. By default, 250,000 descriptors will be extracted (no matter how many training images; the number of descriptors per image is computed automatically so the total of 250,000 is reached). This is the number of descriptors needed to construct a codebook of size 4,096.” Our experiments with their tool required around 8 hours per iteration, probably because of better processors. The main point to stress is that the time required to complete a k-majority iteration with 250,000 ColorORB descriptors (again with a codebook of size 4,096) required on average 16 seconds. This is 1800 times faster. Of course we still need to train the SVM classifiers, which require days to be trained.
The fast computation of the ORB descriptor distances, may be observed also at classification time, because the descriptor quantization step for the image under analysis is done with Hamming distance.
Conclusions
We described a technique to employ fast lightweight features in image description tasks, using concept detection as our benchmark application. Even if the retrieval performance are lower then state of the art techniques, we still get usable results with significantly lower computational requirements. This makes feasible to apply BoW approaches in cases where its complexity made it impossible, such for example on mobile devices.
References
- K. E. A. van de Sande and C. G. M. Snoek, “The university of amsterdam’s concept detection system at imageclef 2011,” in CLEF (Notebook Papers/Labs/Workshop), V. Petras, P. Forner, and P. D. Clough, eds., 2011.
- J. Wu and J. M. Rehg, “Centrist: A visual descriptor for scene categorization.,” IEEE T Pattern Anal 33(8), pp. 1489–1501, 2011.
- E. Rublee, V. Rabaud, K. Konolige, and G. Bradski, “Orb: An efficient alternative to sift or surf,” in International Conference on Computer Vision, (Barcelona), 2011.
- D. Lowe, “Object recognition from local scale-invariant features,” in IEEE Int Conf Comput Vis, 2, pp. 1150– 1157, 1999.
- K. E. A. van de Sande, T. Gevers, and C. G. M. Snoek, “Evaluating color descriptors for object and scene recognition,” IEEE T Pattern Anal 32(9), pp. 1582–1596, 2010.
- H. Bay, A. Ess, T. Tuytelaars, and L. Van Gool, “Speeded-Up Robust Features (SURF),” Comput Vis Image Und 110(3), pp. 346–359, 2008.
- H. Jegou, M. Douze, C. Schmid, and P. Pérez, “Aggregating local descriptors into a compact image representation.,” in IEEE International Conference on Computer Vision and Pattern Recognition, pp. 3304–3311, IEEE, 2010.
- M. Calonder, V. Lepetit, C. Strecha, and P. Fua, “BRIEF: Binary Robust Independent Elementary Features,” in European Conference on Computer Vision, pp. 778–792, Springer, 2010.
- E. Tola, V. Lepetit, and P. Fua, “Daisy: An efficient dense descriptor applied to wide-baseline stereo.,” IEEE T Pattern Anal 32(5), pp. 815–830, 2010.
- S. N. Sinha, J.-M. Frahm, M. Pollefeys, and Y. Genc, “Feature tracking and matching in video using programmable graphics hardware.,” Mach. Vis. Appl. 22(1), pp. 207–217, 2011.
- P. Indyk and R. Motwani, “Approximate nearest neighbors: towards removing the curse of dimensionality,” in Proceedings of the thirtieth annual ACM symposium on Theory of computing, STOC ’98, pp. 604–613, 1998.
- H. Jegou, M. Douze, and C. Schmid, “Product quantization for nearest neighbor search,” IEEE T Pattern Anal 33, pp. 117–128, 2011.
- A. Oliva and A. Torralba, “Modeling the shape of the scene: A holistic representation of the spatial envelope.,” International Journal of Computer Vision 42(3), pp. 145–175, 2001.
- N. Dalal and B. Triggs, “Histograms of oriented gradients for human detection,” in IEEE International Conference on Computer Vision and Pattern Recognition, pp. 886–893, 2005.
- E. Rosten and T. Drummond, “Machine learning for high-speed corner detection,” in In European Conference on Computer Vision, pp. 430–443, 2006.
- C. Harris and M. Stephens, “A combined corner and edge detector,” in Proceedings of the 4th Alvey Vision Conference, pp. 147–151, 1988.
- P. L. Rosin, “Measuring corner properties.,” Computer Vision and Image Understanding 73(2), pp. 291–307, 1999.
- R. Zabih and J. Woodfill, “Non-parametric local transforms for computing visual correspondence,” in Proceedings of the Third European Conference-Volume II on Computer Vision - Volume II, pp. 151–158, Springer-Verlag, (London, UK, UK), 1994.
- P. Heckbert, “Color image quantization for frame buffer display,” in ACM SIGGRAPH, pp. 297–307, 1982.
- C. Grana, D. Borghesani, and R. Cucchiara, “Class-based color bag of words for fashion retrieval,” in IEEE International Conference on Multimedia and Expo, (Melbourne, Austrialia), July 2012.
- L. Kaufman and P. Rousseeuw, “Clustering by means of medoids,” in Statistical Data Analysis Based on the L1-Norm and Related Methods, Y. Dodge, ed., pp. 405–416, North-Holland, 1987.
- H. Mueller, P. Clough, T. Deselaers, and B. Caputo, ImageCLEF, Experimental Evaluation in Visual Information Retrieval, vol. 32 of Lecture Notes in Computer Science: The Information Retrieval Series, Springer, 2010.