А. Ю. Ковалев, В. И. Степанов, Р. Н. Хамитов – Моделирование переходных процессов асинхронных электрических двигателей

Рассматривается расчет переходных процессов асинхронных электрических двигателей согласно трехконтурной схеме замещения, которая учитывает эффекты насыщения магнитной системы и вытеснения токов в стержнях ротора. Данная задача приобретает существенное значение в связи с широким внедрением преобразовательной техники, реализацией на ее основе сложных режимов управления АЭД, работающих в составе комплексов железнодорожной техники, нефтепромыслового оборудования и т. д., а также с реализацией таких специфичных режимов работы АЭД, как режимы расклинивания, толчка, реверса.

Схема замещения для одной фазы АЭД изображена на рисунке 1.

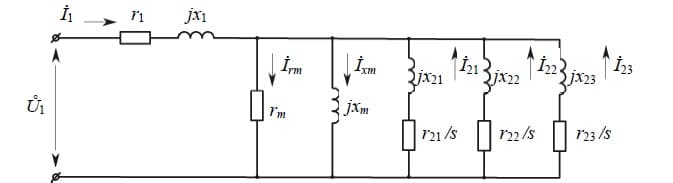
Рисунок 1 – Трехконтурная схема замещения АЭД

На схеме замещения отмечены: rm, r1, r21, r22, r23; xm = ?1Lm, x1 = ?1L1, x21 = ?1L21, x22 = ?1L22, x23 = ?1L23 – активные и индуктивные сопротивления контура намагничивания, цепи статора и трехконтурной схемы замещения ротора соответственно; Lm, L1, L21, L22, L23 – индуктивности, соответствующие потокам рассеяния обмоток статора и ротора; Irm, Ixm, I1, I21, I22, I23 – комплексные действующие значения токов соответствующих ветвей; U1 – фазное напряжение, приложенное к АЭД.

Уравнения математической модели АЭД в рассматриваемом случае содержат следующие элементы: уравнения контуров в соответствии со вторым законом Кирхгофа, узловые уравнения в соответствии с первым законом Кирхгофа, уравнения для потокосцеплений ?s,?r1, ?r2, ?r3, в функции тех токов is, ir1, ir2, ir3, ixms, irms, которые создают рассматриваемые потоки, уравнения для электромагнитного момента Me и момента сопротивления Mn, где индексы s и r обозначают соответствующие фазы статора и ротора: s = {A,B,C}; r = {a,b,c}. В результате математическая модель переходных процессов АЭД приобретает вид смешанной дифференциально-алгебраической системы уравнений. Такого рода математические модели использовались в электромеханике давно, получили признание специалистов, введены в работе [1], носят название математических моделей в канонической форме:

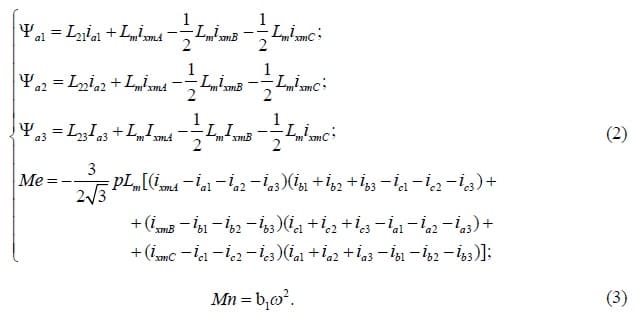
В формулах (1) – (3) ?1 – угловая частота напряжения сети; ?* – относительная частота вращения ротора двигателя; ? – угловая частота вращения ротора двигателя; ? – угол поворота ротора относительно неподвижного статора; p – число пар полюсов; J – динамический момент инерции; b1 – коэффициент. Аналогично записываются системы дифференциально–aлгебраических уравнений для фаз статора B, C и ротора – b, c.

В качестве численного метода расчета переходных процессов согласно каноническим моделям типа приведенной выше (1) – (4) используются адекватные данным моделям численные канонические методы, схема которых приведена в работах [1, 2].

Результаты расчета численными каноническими методами в соответствии с каноническими моделями (1) – (4) приведены на рисунках 2 и 3. Рассматривался погружной асинхронный электрический двигатель ПЭДН–32–117–1000 с параметрами: r1 = 1,359722, x1 = 3,027433515, rm = 413,3696259, xm = 58,47850363, r21 = 2,356210282, x21 = 5,636317755, r22 = 19,64839744, x22 = 13,45779688, r23 = 1,997984871, x23 = 4,927932819, Um = 816,497, ?1 = 314,159, J = 0,455, p = 1, b1 = 0,000803234, определенными согласно методике, предложенной в работе [3].

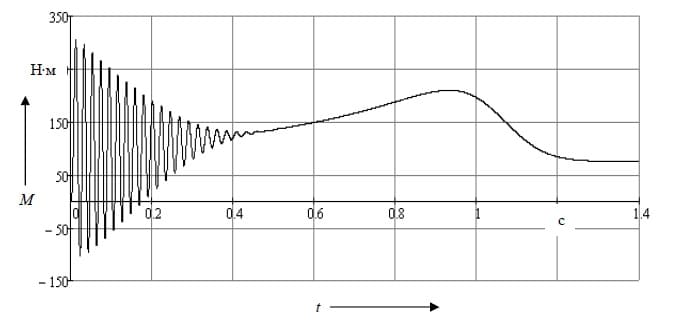
Рисунок 2 – Зависимость электромагнитного момента АЭД от времени в переходном процессе

Рисунок 3 – Зависимость частоты вращения АЭД от времени в переходном процессе

Таким образом, рассмотренная математическая модель в канонической форме, численные канонические методы и результаты вычислительного эксперимента показывают работоспособность предложенного аппарата расчета переходных процессов АЭД для исследовательских целей применительно к установкам электроцентробежных насосов.

Список литературы

Ковалев, Ю. З. Разработка алгоритмов исследования динамики обобщенного электромеханического преобразователя электроэнергии на ЭВМ [Текст] / Ю. З. Ковалев: Автореферат дис. д.т.н. М., 1980. – 32 с.
Ковалев, Ю. З. Методы решения динамических задач электромеханики на ЭВМ: Учебное пособие [Текст] / Ю. З. Ковалев / Омский гос. техн. ун–т. – Омск, 1984. – 84 с.
Ковалев, А. Ю. Электротехнологические установки насосной эксплуатации скважин: Монография [Текст] / А. Ю. Ковалев, Ю. З. Ковалев, А. С. Солодянкин / Нижневартовский гос. гуманитарный ун–т. – Нижневартовск, 2010. – 105 с.