Сравнительный анализ алгоритмов расчета параметров схемы замещения асинхронного двигателя по каталожным данным
Автор: Горячев О.В. Степочкин А.О.
Источник: https://cyberleninka.ru/
Автор: Горячев О.В. Степочкин А.О.
Источник: https://cyberleninka.ru/
Рассматриваются алгоритмы, позволяющие определить параметры схемы замещения по минимальному набору каталожных данных. На основании полученных результатов выполняется моделирование прямого пуска двигателя.
Ключевые слова: асинхронный двигатель, Г-образная схема замещения асинхронного двигателя;каталожные данныеасинхронного двигателя, модель прямого пускаасинхронного двигателя в Simulink.
Как для учебного процесса, так и для прикладных и исследовательских задач очевидна потребность в эффективной методике моделирования режимов работы асинхронного двигателя на основе его математической модели и известных каталожных данных. Система MATLAB с пакетом расширения Simulink дает широчайшие возможности для анализа и синтеза систем управления и их элементов.
Математическая модель асинхронной машины хорошо известна. Она включает в себя модель электрической части, которую можно представить в виде модели пространства состояний четвертого порядка и модель механической части в виде системы второго порядка. Но, вместе с тем, задача выбора простой и точной методики расчета параметров схемы замещения асинхронного двигателя остаётся по-прежнему актуальной, не смотря на большое количество публикаций на эту тему. В данной статье рассматриваются различные алгоритмы такого расчета в применении к конкретной модели асинхронного двигателя, а на основе полученных результатов выполняется визуальное имитационное моделирование прямого пуска двигателя в пакете Simulink.
В каталогах, как правило, приводятся следующие данные двигателя:
–номинальная механическая мощность
–коэффициент полезного действия в номинальном режиме
–коэффициент мощности
–частота вращения в номинальном режиме
–синхронная частота вращения
–номинальное скольжение
–кратность максимального момента
–кратность пускового момента
–кратность пускового тока
Расчетные значения параметров упрощенной Г-образной схемы замещения также являются справочными данными, однако параметры эти присутствуют далеко не во всех каталогах.
–главное индуктивное сопротивление
–активное сопротивление обмотки статора
–приведенное к обмотке статора, активное сопротивление обмотки ротора
–приведенное к обмотке статора, индуктивное сопротивление обмотки ротора
Данные параметры представлены в относительных единицах.
В общем случае, задача расчета параметров схемы замещения (в размерностях системы СИ) может быть поставлена как с известными параметрами Г–образной схемы замещения, так и без них.
Рассмотрим несколько существующих методик расчета.
В [1] представлена достаточно простая и обеспечивающая требуемую точность методика расчета параметров схемы замещения асинхронного двигателя без использования параметров Г–образной схемы замещения и с предполагаемой погрешностью не более 15%. Однако для её реализации требуются исходные данные, которые в каталогах, как правило, отсутствуют. Это энергетические показатели при нагрузке двигателя равной 25, 75, 50 и 125% от номинальной. Соответственно, в нашем случае применение данной методики является затруднительным.
Методика, представленная в работе [2] также позволяет рассчитать параметры схемы замещения двигателя в единицах системы СИ без использования параметров Г-образной схемы замещения.
Для выполнения расчета определяются основные зависимости.
Номинальное фазное напряжение при схеме соединения обмотки звезда (В):
Критическое скольжение (о.е.):
Номинальная угловая частота вращения (рад/c):
Номинальный момент вращения (Нм):
Пусковой момент (Нм):
Делается оценочное допущение о величине механических потерь в двигателе:
Вводится расчетный коэффициент С (о.е.):
И из зависимости для расчета полной потребляемой мощности мы получаем приведенное активное сопротивление ротора (Ом):

и активное сопротивление статора(Ом):
Аналогично, на основе принятых автором [2] допущений получаются зависимости для расчета приведенных индуктивностей рассеяния статора и ротора (Гн):

индуктивности статора (Гн):
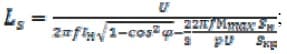
индуктивности цепи намагничивания (Гн):
При выполнении предварительного расчета по предложенной схеме, к сожалению, не удалось добиться желаемой точности, поэтому применение данной методики в наших условиях будем считать нецелесообразным.
Рассмотрим методику расчета с применением известных параметров Г–образной схемы замещения.
Параметры математической модели вычисляются по следующему алгоритму:
Вычисляются значения индуктивного и активного сопротивлений статора:

Определяется номинальный фазный ток статора:
Осуществляется переход к действительным значениям параметров схемы замещения:
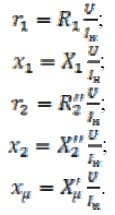
Происходит переход от индуктивных сопротивлений к индуктивностям

Определяем индуктивности статора и ротора
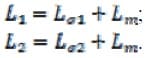
Данный алгоритм является самым простым из перечисленных выше и, одновременно, обеспечивает требуемую в нашем случае точность.
Выполним расчет по данному алгоритму для конкретной марки двигателя.
–номинальная механическая мощность cosf=0,9;
–частота вращения в номинальном режиме nн=1475 об/мин;
–синхронная частота вращения nc=1500 об/мин;
–кратность максимального момента λ=2,5;
–кратность пускового момента Кп=1,4;
–кратность пускового тока Iп=7;
–главное индуктивное сопротивление Xм=4,4;
–активное сопротивление обмотки статора R'1=0,039;
–индуктивное сопротивление рассеяния обмотки статора X'1=0,086
–приведенное к обмотке статора, активное сопротивление обмотки ротора R''2=0,018;
–приведенное к обмотке статора, индуктивное сопротивление обмотки ротора X''2=0,14.
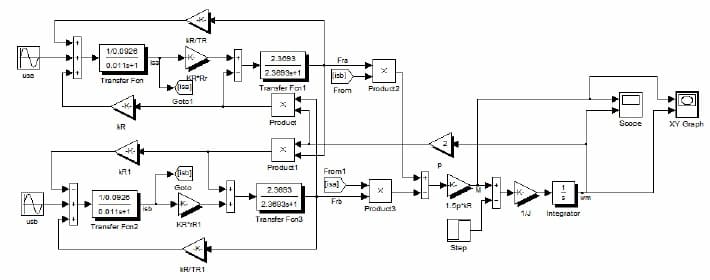
Рисунок 1 – Модель прямого пуска двигателя А200М4У3 в пакете Simulink

Рисунок 2 – Переходные процессы по скорости и моменту на валу двигателя А200М4У3 при прямом пуске
В результате получим следующие параметры схемы замещения двигателя:
–активное сопротивление обмотки статора Rs=0,0739 Ом;
–индуктивность обмотки статора Ls=0,0453 Гн;
–приведенное к обмотке статора, активное сопротивление обмотки ротора Rr=0,0191 Ом;
–приведенная к обмотке статора, индуктивность обмотки ротора Lr=0,0453 Гн;
–индуктивность цепи намагничивания Lm=0,0448 Гн;
После расчета параметров схемы замещения с помощью полученных данных выполним моделирование прямого пуска двигателя А200М4У3 в пакете Simulink согласно методике из публикации [3]. Используем модель двигателя в неподвижной системе координат (рис. 1 и 2).
В заключение отметим, что все представленные методики имеют свои достоинства и недостатки, и основополагающим моментом при выборе будет, прежде всего, являться набор исходных каталожных данных, а точнее – известны ли параметры Г–образной схемы замещения. В случае, если данные параметры заданы, лучшим выбором станет последняя из рассмотренных методик расчета.
Список литературы