Аннотация
В работе рассматриваются вопросы разработки дискретной одноконтурной следящей системы регулирования положения для двигателя постоянного тока с постоянными магнитами. Приведена методика синтеза ПД-регулятора положения в непрерывном виде. Показана эффективность предложенной методики при переходе к дискретной системе регулирования.
Системы регулирования положения делятся на две большие группы: системы позиционирования и следящие системы. Задача первых – перемещение из точки А в точку Б с желаемым характером изменения координат двигателя (ток, скорость, положение). Вторые системы ориентированы на следование заранее неизвестной траектории с минимальным отклонением. Исходя из этого к следящим системам предъявляются повышенные требования с точки зрения быстродействия .
Традиционный метод синтеза трехконтурной системы регулирования положения при работе не даёт достаточного быстродействия системы при работе от внешнего задающего устройства. Следовательно, необходимо применить иной подход к синтезу. В источниках рассматривается синтез пропорционально-дифференцирующего регулятора положения для электропривода одного из звеньев робота манипулятора. Следует отметить, что для такой задачи использовался сервопривод, имеющие более высокие динамические характеристики по сравнению с обычными двигателями постоянного тока. Таким образом, указанную методику необходимо предварительно протестировать на компьютерной модели двигателя постоянного тока.
Основной сложностью при синтезе системы автоматического регулирования для данного двигателя является невозможность точного определения его параметров. Особенно это касается электромагнитной постоянной времени якоря, которая в силу своей незначительности практически не оказывает влияния на форму графиков переходных процессов по скорости.
С целью упрощения математической модели объекта регулирования примем известное допущение, что на начальном интервале времени переходная функция апериодического звена незначительно отличается от таковой интегрирующего звена. Исходя из этого структурную схему объекта регулирования можно представить в виде, показанном на рис.1.

Рисунок 1 – Объект управления
Синтез следящей системы позиционирования осуществляется на основании приведения передаточной функции замкнутой системы к некоторому эталонному виду. Поскольку пропорционально-дифференцирующий регулятор не оказывает влияния на порядок системы, эталонной моделью будем считать колебательное звено с постоянной времени Т, отвечающей требованиям к быстродействию электропривода, и коэффициентом демпфирования:
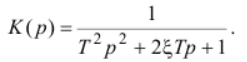
Структурная схема рассматриваемой системы приведена на рис.2.

Рисунок 2 – Следящая система позиционирования с ПД-регулятором
Передаточная функция такой системы имеет вид:

Исходя из требования совпадения в численном виде коэффициентов передаточных функций, получим следующие значения коэффициентов ПД-регулятора:

На рис.3 приведены графики переходных процессов в такой системе при отработке четырех типов задающих воздействий, а на рис.4 – графики ошибки позиционирования. Величина желаемой постоянной времени принято равным 0,5 мс.
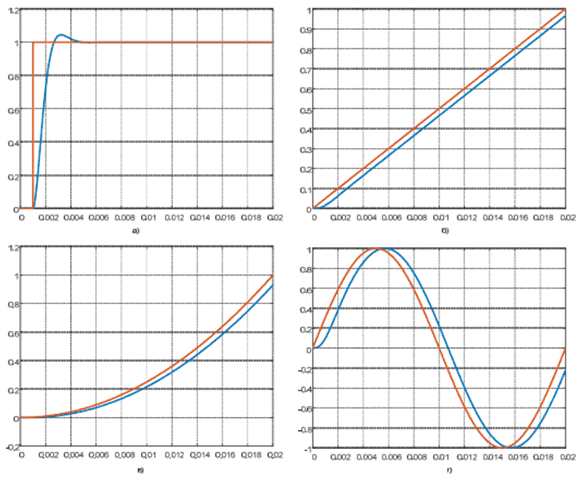
Рисунок 3 – Заданная (красная линия) и реальная (синяя линия) траектории движения при отработке стандартных воздействий
Очевидно, что показатели качества переходных процессов соответствуют ожиданиям. При отработке сигналов сложной формы наблюдается динамическая ошибка, обусловленная суммарным запаздыванием при отслеживании траектории, не превышающим 1 мс.
Проверим качество работы разработанной системы автоматического управления на более реальной модели объекта.
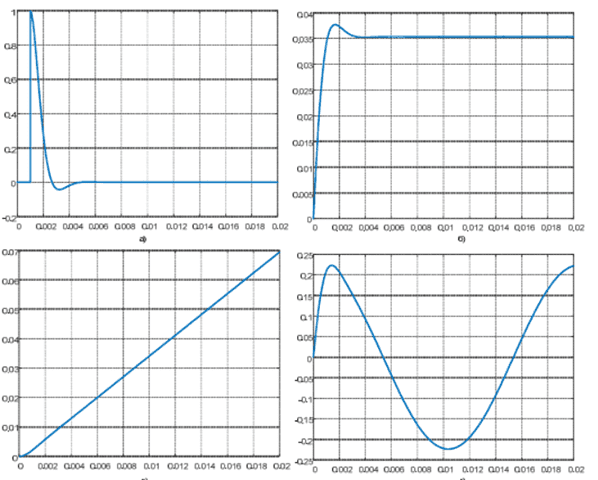
Рисунок 4 – Ошибка отработки стандартных воздействий
Дополним структурную схему рис.1 двумя апериодическими звеньями с постоянной времени, равной 0,1 мс, в качестве имитации силового преобразователя и якорной цепи двигателя. Также учтем влияние ЭДС якоря.
Результаты моделирования приведены на рис.5. Очевидно, что качество переходных процессов ухудшилось несущественно, что говорит о возможности применения указанной методики для синтеза следящих систем позиционирования.
Выводы
В случае, если электромагнитная инерционность значительно меньше механической, модель двигателя постоянного тока можно существенно упростить, применив известные методики синтеза следящих систем позиционирования. Открытым остаются вопросы повышения быстродействия таких систем, а также их восприимчивость к параметрическим неопределенностям и влияниям возмущающих воздействий.
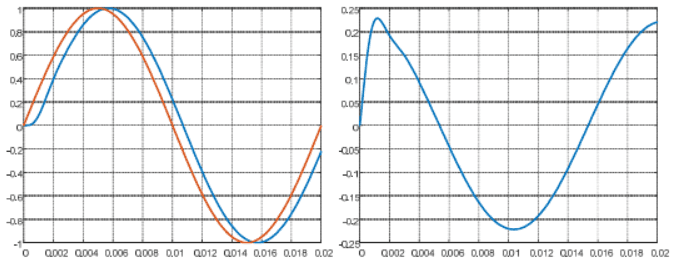
Рисунок 5 – Отработка синусоидального воздействия следящей системой с уточненной моделью объекта управления
БИБЛИОГРАФИЯ
1. Васильев К.К. Теория автоматического управления (следящие системы):
Учебное пособие. 2-е изд. – Ульяновск, 2001. – 98 с
2. Борисов О.И. Методы управления робототехническими приложениями.
Учебное пособие / О.И. Борисов, В.С. Громов, А.А. Пыркин. — СПб.: Университет
ИТМО, 2016. — 108 с.