Реферат по теме выпускной работы
Содержание
- Введение
- 1 Оптимальное управление потоками мощности в неоднородных электрических сетях с дальними электропередачами
- 1.1 Метод формирования законов оптимального управления потоками мощности в электрических системах на основании анализа их неоднородности
- 1.2 Совершенствование метода формирования законов оптимального управления нормальными режимами электрических систем с дальними электропередачами
- 1.3 Особенности реализации системы автоматического управления потоками мощности в эс с децентрализацией функции управления в реальном времени
- 2 Оптимизация потокораспределения активных мощностей
- 3 Оптимальное распределение потоков мощности в замкнутых сетях
- Выводы
- Перечень использованных источников
Введение
Одним из основных показателей эффективности использования электроэнергии являются технологические расходы, связанные с ее транспортировкой от источников питания к потребителям.
Главной причиной повышенного расхода электроэнергии, в частности технической составляющей потерь, является низкая эффективность электросберегающих мероприятий, что, в свою очередь, обусловлено недостаточным уровнем автоматизации контроля и управления режимами магистральных и распределительных электросетей. Учитывая высокий уровень развития современных микропроцессорных систем и широкомасштабное внедрение автоматизированных систем мониторинга режимов, особенно магистральных электросетей, становится возможным использовать информацию из баз данных таких систем в задачах оптимизации управления потоками мощности и взаимовлияния электрических сетей в электрической системе (ЭС).
Автоматизация оптимального управления потоками мощности в современных ЭС, развиваясь на базе существующих автоматизированных систем диспетчерского управления (АСДУ), предусматривает разработку и усовершенствование технического, информационного и программного обеспечения. На сегодняшний день в практике диспетчерского управления энергосистемами используют программно-технические средства оптимизации нормальных режимов ЭС, которые имеют ряд недостатков. Несовершенство математически–программного обеспечения обусловлено, преимущественно, с использованием упрощенных математических моделей процессов транспортировки электроэнергии, которые были актуальными 20 – 30 лет назад и не соответствуют современному уровню аппаратного обеспечения. В составе аппаратного обеспечения практически отсутствуют специализированные информационные устройства связи между регулирующими устройствами и управляемыми электронно–вычислительными машинами (ЭВМ). А без таких устройств невозможно взаимодействие программных средств оптимального управления режимами электрических сетей и регулирующих устройств (РУ). Кроме того, автоматизированные системы, обеспечивающие локализацию отдельных функций централизованного управления, реализуя программное управление с местными параметрами и оперативную коррекцию наладочных параметров локальных систем автоматического управления (САУ), способны повысить надежность функционирования системы в целом и расширить ее функциональность в особых режимах работы.
1 Оптимальное управление потоками мощности в неоднородных электрических сетях с дальними электропередачами
1.1 Метод формирования законов оптимального управления потоками мощности в электрических системах на основании анализа их неоднородности
Компенсировать дополнительные потери мощности и электроэнергии в ЭС, обусловленные ее неоднородностью, можно путем регулирования напряжения в узлах ЭС или введением в контуры уравнительных э. д. с.. При такой постановке задачи управляемыми переменными являются э. д. с., которые необходимо ввести в замкнутые контуры для реализации оптимального токораспределения за счет изменения коэффициентов трансформации трансформаторов, входящих в эти контуры. [1].
Оптимальное значение потерь в ЭС достигается при относительных значениях э. д. с., которые рассчитывают по формулам:
| Е*ур.а(t) = πEa × J*p(t); | (1.1) | |
| Е*ур.р(t) = πEр × J*а(t); |
где Е*ур.а(t), Е*ур.р (t) – векторы активных и реактивных составляющих относительных значений уравнительных ЭДС; J*а(t), J*p(t) – векторы активных и реактивных составляющих относительных значений токов в узлах.
В (1.1) все параметры поданы в относительных единицах. Как базисные принимаются параметры идеального режима, рассчитанного по r–схеме замещения ЭС.
Матрицы критериев подобия определяют по формулам:
 |
(1.2) |
где xк, rк – активная и реактивная составляющие матрицы контурных сопротивлений для системы базисных контуров; Мa, Na – матрицы соединений веток дереве схемы замещения ЭС, соответственно, в узлах контурах [2].
Соотношения (1.1) являются законами оптимального управления, в которых коэффициенты обратной связи по физическому смыслу – критерии подобия. Для реализации законов управления разработана система автоматического управления (САУ) нормальными режимами ЭС, основная функция которой заключается в том, чтобы поддерживать значение комплексного критерия оптимальности F*, в котором учтены факторы надежности и экономичности транспортировки электроэнергии, а также ее качества, в пределах установленной зоны нечувствительности δF* (управляющие воздействия регулирующими устройствами осуществляются после выхода критерия за ее пределы). Результатом действия системы является приближение текущей траектории изменения потерь мощности в ЭС к оптимальной по заданным эксплуатационным условиям. Кроме того, реализация управляющих воздействий, полученных на основании (1.1) [2], обеспечивает оптимизацию взаимовлияния магистральных и распределительных электросетей по потерям и уровням напряжений.
1.2 Совершенствование метода формирования законов оптимального управления нормальными режимами электрических систем с дальними электропередачами
Для компенсации негативного влияния неоднородности параметров электросетей за счет управления РУ в контуры необходимо ввести ЭДС небаланса, за счет чего токи небаланса Iнб частично или полностью компенсируют фиктивные уравнительные токи Iур. В общем случае для j–го контура, принадлежащего таким образом системе базисных контуров, ЭДС небаланса определяют [3]:
 |
(1.3) |
где ki – коэффициент трансформации i–го трансформатора, принадлежащий множеству трансформаторов j–го контура ТРj; Uб – напряжение базисного узла ЭС.
Фиктивные уравнительные ЭДС в неоднородных электросетях, содержащие трансформаторные связи и дальние электропередачи как функции природного и экономического токораспределения, можно определить по выражению (1.5). Выражения для определения векторов при наличии нескольких балансирующих узлов в электросетях могут быть представлены следующим образом [3]:
 |
(1.4) | |
 |
(1.5) |
где NAk – матрица связей веток ЭС в её контурах, построенная с учётом трансформаторных связей и дальних электропередач; ZB – диагональная матрица сопротивлений ветвей схемы замещения, в которой ветки дальних передач представлены постоянными четырёхполюсника В; Iэк – вектор экономических токов в ветвях схемы замещения электросетей, определенный на основании расчёта экономического режима электросетей с дальними ЛЭП; I – вектор токов в ветвях, что соответствует реальному токораспределению с учётом взаимовлияния электросетей различных классов напряжения, которые работают параллельно.
Подставив в (1.5) выражения (1.4), после преобразований и упрощений получим [4]:
| Eзр = E*нбк × Ub − j × (E*нбγUb + Zф.урJ); | (1.6) |
где E*нбк &ndash матрица относительных контурных ЭДС.
Из (1.6) видно, что составляющие E*нбγ и Zф.ур определяются соотношением реактивных и активных сопротивлений ветвей схемы замещения ЭС [5], коэффициентами трансформации и коэффициентами распространения волны дальних передач (в виде постоянных четырёхполюсника А). Следовательно, отсутствие уравнительных ЭДС в замкнутых контурах характерно только для электросетей, в которых коэффициенты трансформации в контурах сбалансированы, все ветки соответствуют классическому условию однородности, а для дальних ЛЭП обеспечивается условие согласованности коэффициентов распространения волны. Исходя из последнего обеспечить однородность электросетей с дальними ДЭП практически невозможно, а для обеспечения режимов их работы, близких к экономическим, необходимо оптимальное управление трансформаторами связи с продольно-поперечным регулированием.
1.3 Особенности реализации системы автоматического управления потоками мощности в ЭС с децентрализацией функции управления в реальном времени
Для реализации системы автоматизированного управления потоками мощности и напряжением в электрических системах, которая обеспечивала бы возможности оперативного управления, целесообразно использовать классическую двухконтурную схему с децентрализацией функций управления в реальном времени [5]. На первом этапе (в контуре централизованного управления) определяют причины неоптимального функционирования ЭС и перечень доступных регулирующих устройств. Для этого выполняют ретроспективный анализ результатов управления режимами на основании краткосрочного планирования, а также оценивают показатели неоднородности ЭС. Далее, используя полную информацию о параметрах ЭС, определяют и корректируют матрицы условно постоянных параметров. С использованием разработанных математических моделей осуществляют адаптацию законов управления в реальных условиях функционирования регулирующих устройств, выполняют ранжирование регулирующих устройств по приоритету управления с учетом надежности и ресурса устройств РПН. Определяют зоны нечувствительности локальных систем управления регулирующими устройствами, что позволяет установить рациональную интенсивность переключений для каждого трансформатора и скоординировать их работу во время оперативного управления таким образом, чтобы снижение потерь мощности достигалось при минимальном количестве переключений.
На втором этапе (в контуре локального управления) полученные математические модели используют для определения расчетного значения управляющих воздействий и принятия решения о целесообразности их реализации. Управление в темпе процесса осуществляют только в контуре оперативного управления. Во внешнем контуре, при необходимости, может осуществляться корректировка пассивных параметров ЭС. Однако такое изменение чаще осуществляется на стадии краткосрочного планирования режимов после значительных изменений нагрузок или существенных отклонений параметров регулирующих устройств от плановых [6, 7].
Подобная схема реализации системы управления позволяет обеспечить децентрализацию части информационных функций без потери принципов централизованного управления, поскольку в течение основного времени (режимы нормальной эксплуатации ЭС) регулирование параметров трансформаторов осуществляется на основании локальных параметров, обеспечивая условный оптимум общесистемного критерия оптимальности. Отклонение пассивных параметров ЭС или параметров режима централизованно контролируют и при необходимости корректируют отдельные параметры моделей. Следовательно, по сути реализуется централизованное оперативное управление режимами ЭС с помощью децентрализированных
подсистем – локальных регулирующих устройств на отдельных трансформаторных подстанциях (электростанциях) [7].
Автоматическое управление РУ ЭС и согласование управляющих воздействий с оперативным управлением выполняют с использованием микропроцессорного устройства автоматического контроля и управления функционированием (АКУФ) РУ (рис. 1.1). Устройство может работать в трех основных режимах:
- получение закона с управляющей ЭВМ и управления согласно ему (при наличии в достаточном количестве достоверной информации о состоянии электрической сети);
- введение из центральной системы управления номера отпайки и установки ее на регуляторе РПН трансформатора (при отсутствии должного информационного обеспечения или дистанционного управления диспетчером энергосистемы);
- автономная работа устройства в режиме стабилизации вторичного напряжения трансформатора или автотрансформатора на заданном уровне с учетом введенной зоны нечувствительности, или автономная реализация встречного регулирования напряжения.

Рисунок 1.1 – Внешний вид устроства АКУФ РУ (вид спереди)
Для перевода АКУФ РУ из состояния ожидания в активное состояние средствами АСУ подстанции через блок связи передают код операции. После этого устройство проверяет параметры РПН для идентификации крайних положений: полученную информацию записывают в оперативное запоминающее устройство (ОЗУ). В зависимости от кода операции устройство переводят в соответствующий режим работы.
При необходимости установить определенную отпайку регулятора РПН сначала через блок связи осуществляют ввод ее номера от управляющей ЭВМ. В случае несовпадения номера новой отпайки с номером установленной, определяют знак управляющего сигнала (направление переключения РПН). Далее управляющие импульсы поступают в регистры блока контроля и управления РПН; соответствующие реле замыкаются – и начинается переключение. Устройство переходит в режим ожидания окончания переключения, контролируя соответствующие каналы блока контроля и управления РПН. После окончания переключения управляющие импульсы снимают, измеряют параметры объекта управления, проверяют соответствие их заданным ограничениям и снова сравнивают номера отпаек. Процесс повторяется, пока на регуляторе РПН не установится необходимая отпайка. Любые нарушения ограничений по параметрам (токи, напряжения), нарушения в работе устройства или регулирующего устройства в виде сообщений направляются в управляющую ЭВМ [8].
Применение АКУФ РУ позволяет ввести в систему управления нормальными режимами ЭС обратную связь, контролировать выполнение управляющих воздействий и оценивать эффективность управления как отдельными трансформаторами, так и энергосистемой в целом. Последнее дает возможность автоматизировать ряд функций оперативного управления и повысить эффективность использования РУ трансформаторов в задачах уменьшения потерь активной мощности в электрической системе.
2 Оптимизация потокораспределения активных мощностей
Современные электрические сети имеют естественное потокораспределение: потоки мощности распределяются по параллельным ветвям соответственно комплексным величинам сопротивлений линий, образующих эти пути.
Экономичным называется потокораспределение, соответствующее минимуму потерь активной мощности в сети. Экономичное потокораспределение совпадает с естественным, возникающим в расчётной схеме после исключения из нее реактивных сопротивлений. При экономичном потокораспределении мощности по ветвям распределяются только в соответствии с активными сопротивлениями.
При естественном потокораспределении оптимизация режима энергосистемы производится в двух направлениях. Оптимизируется распределение активных мощностей между станциями по условию минимума суммарного расхода топлива в энергосистеме. Корректируется реактивная мощность линий по условию минимума потерь в сети с учетом ограничений оборудования, установленного диспетчером профиля напряжения и условий устойчивости. При этом потоки активной мощности не меняются или меняются незначительно [8].
Неблагоприятное потокораспределение в развитых высоковольтных сетях связано с неоднородностью сетей – различием индуктивной добротности. Для линий 110 кВ диапазон ID = 1,37–3,34.
Минимальные потери в сети и соответствующее оптимальное распределение потоков активной мощности были бы при условии равенства индуктивных добротностей всех линий, образующих замкнутые контуры. Следовательно, для оптимизации потокораспределения в развитых сетях транзитные потоки в линиях нижних слоев необходимо снизить в несколько раз.
Оптимизация естественного распределения потоков мощности в замкнутых сетях может быть достигнута следующими путями:
- продольным и продольно-поперечным регулированием; включением в контуры установок продольной компенсации; размыкание части контуров замкнутой сети;
- применением вставок постоянного тока (ВПТ); использованием управляемых линий электропередачи; использование гибких электропередач.
На рисунке 2.1 синусоидальное напряжение (красная линия) и ток (зелёная линия) синфазны – между ними нет фазового сдвига (φ = 0°, cosφ = 1) – нагрузка полностью активная, нет реактивной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия).
Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг φ = 90° (cosφ = 0) – нагрузка полностью реактивная, нет активной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны с коэффициентом мощности, равным 0.
Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг φ = 45° (cosφ = 0,71) – нагрузка имеет и активную, и реактивную составляющие. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны из переменного напряжения и тока с коэффициентом мощности, равным 0,71.
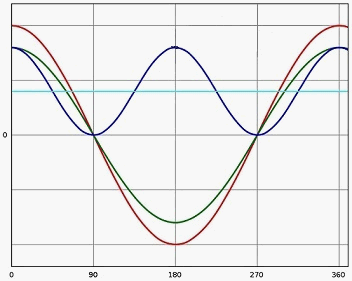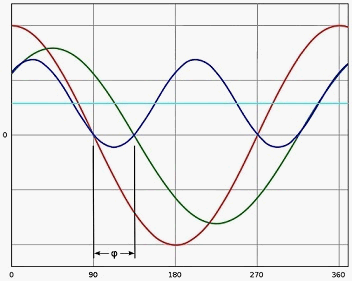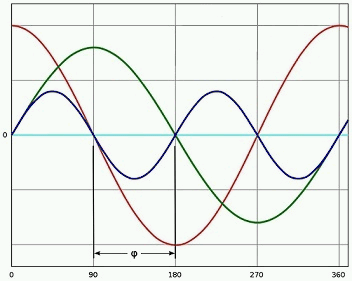
Рисунок 2.1 – Фазовый сдвиг между синусоидальным напряжением и током
(анимация: 3 кадра, 7 циклов повторения, 56 килобайт)
(Красная кривая – напряжение; зелёная кривая – ток; синяя кривая – мощность; голубая кривая – средняя мощность; φ – угол сдвига между фазами)
3 Оптимальное распределение потоков мощности в замкнутых сетях
Оптимизация распределения мощностей в замкнутом контуре – это частная задача оптимизации режима электрической сети. Будем считать, что в узлах сети заданы неизменные токи, т. е. уравнения установившегося режима линейны. Если в узлах заданы неизменные мощности, то они определяются по номинальному напряжению [9]:
 |
(3.1) |
где Sk и Ik – заданные комплексные мощность и ток в каждом узле; Un – номинальное напряжение сети.
При этом ток в ветви kj определяется следующим образом:
 |
(3.2) |
При выполнении условий (3.1) или (3.2) уравнения установившегося режима остаются линейными, то есть вместо заданных комплексных токов в узлах можно использовать комплексные мощности в узлах, а вместо токов в ветвях - мощности в ветвях.
Найдем распределение мощностей в сети на рисунке 3.1, соответствующее наименьшим потерям активной мощности, при выполнении первого закона Кирхгофа для мощностей при условии (3.1). Иными словами, определим такие значения мощностей S12, S13, S23, которые соответствуют минимуму потерь активной мощности в сети.
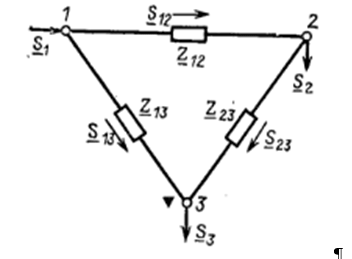
Рисунок 3.1 – Схема замкнутой сети
При выполнении следующих ограничений-равенств первого закона Кирхгофа для активных и реактивных мощностей:
 |
(3.3) |
Потери активной мощности в сети (рис. 3.1) с учётом условия (3.2) равны:
 |
Условие минимума потерь:
 |
(3.4) |
Потери мощности, записанные в виде (3.4), это целевая функция задачи оптимизации режима сети, условия (3.3).
Система ограничений (3.3) содержит четыре уравнения и шесть неизвестных активных и реактивных потоков мощности в ветвях Р12, Р13, Р23, Q12, Q13, Q23.. Она имеет бесконечное множество решений. Можно задать любые значения, например, четырех потоков Р13, Р23, Q13, Q23 и из (2.3) найти значения потоков Р12, Q12, удовлетворяющие первому закону Кирхгофа. Параметры режима имеют две степени свободы. Изменяя параметры режима, можно найти такие их значения, при которых потери мощности ΔР в сети минимальны [8].
Установившийся режим простой замкнутой сети описывается не только двумя комплексными уравнениями первого закона Кирхгофа, но и одним комплексным уравнением второго закона Кирхгофа. Осуществлять регулирование и уменьшать ΔР невозможно.
Определим потоки мощности, соответствующие минимуму потерь. Для этого выразим Р12, Р23, Q12, Q23 из (3.3) через неизвестные потоки Р13, Q13 и заданные нагрузки в узлах:
 |
(3.5) |
Подставим (3.5) в целевую функцию (3.4) и выразим потери через два неизвестных потока Р12 и Q12..
 |
(3.6) |
Получили целевую функцию, которая зависит только от двух неизвестных Р12 и Q12. При этом задача определения условного экстремума функции шести неизвестных сведена к отысканию безусловного экстремума функции двух переменных. Как известно, последний определяется из условия равенства нулю частных производных от ΔР по Р12 и Q12. Решив уравнения, в итоге получим следующие аналитические выражения для оптимальных (экономических) потоков мощности Р12 и Q12 [9]:
 |
(3.7) |
Минимум потерь мощности при выполнении первого закона Кирхгофа соответствует распределению мощностей в простой замкнутой сети только с активными сопротивлениями. Это распределение мощностей называется экономическим [10].
Выводы
Генерация реактивной мощности влияет на режим напряжений и потокораспределение мощностей системы. Следовательно, распределение реактивных мощностей также может быть задачей оптимизации.
При комплексной оптимизации любые изменения потоков мощности влияют на узловые напряжения, а значит, изменение потоков активных мощностей влияет на потоки реактивных и наоборот.
При комплексной оптимизации рассматривается полная задача определения режима активных и реактивных мощностей системы. Электрическая сеть представляется таким образом, чтобы получить активные и реактивные мощности по всем необходимым ветвям и узлам. Так как изменения потоков мощности в сети влияют на узловые напряжения, то, значит, изменение потоков активных мощностей повлияет на потоки реактивных и наоборот. Главные трудности комплексной оптимизации заключаются в том, что сочетаются две задачи: оптимального распределения нагрузки между станциями и оптимального режима сетей.
Электрические системы не являются оптимальными с учетом расхода электроэнергии при ее производстве, транспортировке и распределении. Одной из основных причин неоптимальности состояний ЭС является их неоднородность. Обеспечение оптимальности режимов работы ЭС требует применения соответствующих систем автоматического управления.
Применение устройства АКУФ РУ позволяет реализовать в автоматизированной системе оптимального управления нормальными режимами ЭС обратную связь по параметрам управления и обеспечивает возможность децентрализации отдельных задач оперативного управления таких, как адаптация параметров наблюдения, контроль за выполнением управляющих воздействий, оценки целесообразности управления отдельными трансформаторами и т. п. Последнее дает возможность повысить надежность и эффективность использования регулирующих устройств в ЭС.
Список литературы
- Холмский В. Г. Оптимизация потокораспределения в замкнутых электрических сетях с высокой степенью неоднородности / В. Г. Холмский // Электричество. – 1965. – № 9. – С. 16 – 21.
- Веников В. А. Дальние электропередачи переменного и постоянного тока / В. А. Веников, Ю. П. Рыжов. – М.: Энергоатомиздат, 1985. – 272 с.
- Электрические системы и сети / Н.В. Буслова, В.Н. Винославский, Г.И. Денисенко, В.С. Перхач. – К.: Вища шк. Головное издательство, 1986. – 584 с.
- Справочник по проектированию электроэнергетических систем / Под ред. С.С. Рокотяна, И.М. Шапиро. – М.: Энергоатомиздат, 1985. – 352 с.
- Лежнюк. П. Д. Моделирование компенсации влияния неоднородности электрических сетей на экономичность их режимов / П. Д. Лежнюк, В. В. Кулик, Д. І. Оболонський // Электричество. – 2007. – № 11. – С. 2 – 8.
- Рожкова Л. Д., Козулин В. С. Электрооборудование станций и подстанций. – М.: Энергоатомиздат, 1987. – 648 с.
- Справочник по электроустановкам высокого напряжения / Под ред. И.А. Баумштейна и В.М. Хомякова. – М.: Энергоатомиздат, 1981. – 656 с.
- Электрические системы и сети / Н.В. Буслова, В.Н. Винославский, Г.И. Денисенко, В.С. Перхач. – К.: Вища шк. Головное издательство, 1986. – 584 с.
- Справочник по проектированию электроэнергетических систем / Под ред. С.С. Рокотяна, И.М. Шапиро. – М.: Энергоатомиздат, 1985. – 352 с.
- Идельчик В.И. Электрические системы и сети. – М.: Энергоатомиздат, 1989. – 592 с.
