Аннотация
Будущие разработки более легких, компактных и мощных двигателей, обусловленные соображениями экологии и устойчивости в транспортной отрасли, предполагают более высокие нагрузки, токи и электромагнитные поля. Следовательно, возникнут сильные связи между механическими, тепловыми и электромагнитными эффектами, и для конструкции двигателей потребуется последовательный подход к мультифизическому моделированию. Типичное моделирование - большая часть которого представлена в электротехнической литературе - включает пошаговый процесс, в котором разрешение уравнений Максвелла обеспечивает лоренцеву и магнитные силы, которые впоследствии используются как внешние объемные силы для разрешения уравнений движения Ньютона.
В представленной здесь работе предлагается мультифизическая постановка уравнений, управляющих электродвигателями. Используя прямой подход механики сплошных сред, общая структура, объединяющая электромагнитные, тепловые и механические поля, выводится с использованием основных принципов термодинамики. Особое внимание уделяется выводу связанных материальных уравнений для изотропных материалов при малой деформации, но произвольной намагниченности.
Из-за сложной геометрии типичного электродвигателя численные решения основных уравнений необходимы. Чтобы получить представление, эта теория применяется для получения аналитического решения идеализированного асинхронного двигателя, для которого мы рассчитываем электрический ток, магнитные поля, поля напряжений и температуры в зависимости от приложенного тока и параметра скольжения. Различные компоненты тензора напряжений и вектора объемной силы сравниваются с их чисто механическими аналогами из-за инерции, что позволяет количественно оценить значительное влияние электромагнитных явлений.
Ключевые слова: связанные термомеханические и электромагнитные процессы, электродвигатели, континуум механика, аналитические решения.
1. Введение
Растущее значение и доля рынка гибридных и чисто электрических транспортных средств в стремлении сократить их углеродный след, побуждает электромоторную промышленность разрабатывать продукты с более высокими характеристиками и затраты на производство. Новые цели ставятся различными государственными учреждениями и промышленными ассоциациями (Lopez et al., 2019) с точки зрения эффективности, надежности, потерь мощности, удельной мощности, более высокой скорости вращения и уменьшенный вес. Для решения этих технологических проблем необходимы новые конструкции электродвигателей. Для достижения вышеупомянутых технических целей необходимо разработать соответствующие инструменты моделирования.
В конце 90-х годов в электродвигателях появились расчеты напряжений в результате шума и вибрации. обеспокоенность. Как указано Reyne et al. (1987), первой возникшей трудностью была оценка электромагнитные массовые силы, для которых разные авторы давали разные выражения, из-за отсутствия согласованная континуальная электродинамика. Множественность различных формулировок, прямая как Как и вариационный для термомеханико-электромагнитного континуума, это источник путаницы. Разные (хотя и эквивалентные) выражения для напряжения Максвелла и объемных электромагнитных сил могут быть получены и Таким образом, возникают трудности с правильным моделированием напряжений в электродвигателях. Для дальнейшего При обсуждении этого вопроса заинтересованный читатель отсылает к статье Канканалы и Триантафиллидиса. (2004) и книга Hutter et al. (2007). Использованы первые расчеты FEM для напряжений в электродвигателях. ступенчатый, несвязанный подход: электрические токи и магнитные поля рассчитываются с использованием чисто электромагнитная модель; вектор электромагнитной телесной силы был затем введен как внешнее тело сила в чисто механической модели для расчета результирующего напряженного состояния (например, см .: Reyne et al. (1988); Javadi et al. (1995)).
Целью данной работы является термодинамически согласованная формулировка, связывающая электромагнитные тепловые и механические эффекты для краевой задачи электродвигателей. О теоретическом сторона, общие теории механики сплошных сред, связывающие термомеханические и электромагнитные эффекты в твердых телах началась еще в 1950-х и 1960-х годах. Хотя обзор литературы выходит за рамки данного исследования, некоторые комментарии полезны, чтобы рассмотреть данную работу в перспективе. Как и у Fonteyn et al. (2010а, б) моделирование Применяемый здесь подход представляет собой «прямой» метод, который использует законы сохранения механики сплошной среды и процедура термодинамики, введенная Коулманом и Ноллом (1963), чтобы получить основную уравнения и материальные законы; очень удобочитаемый отчет представлен в книге Ковец (2000). За Для интересующих приложений электродвигателей принято упрощение задачи «вихретоковый» (см. Hiptmair and Ostrowski (2005) для обоснования линейных материалов), в котором не учитывается электрическая поляризация. и токи смещения для электрических полей низкой частоты. Эта теория в дальнейшем используется для получения аналитическое решение идеализированного асинхронного двигателя, для которого мы рассчитываем электрический ток, магнитные, напряженные и температурные поля. Тензор напряжений и вектор объемной силы сравниваются с их чисто механические аналоги из-за инерции, количественно определяющие значительное влияние электромагнитных явлений, новинка в этой области, насколько известно автору.
Результаты и обсуждение
Хотя мы решаем идеализированный двигатель, представленные здесь результаты соответствуют материалам, геометрии и рабочие параметры приведены в электротехнической литературе. Введенные безразмерные величины позволяют напрямую сравнивать результаты с соответствующими физически значимыми величинами.
1.1. Плотность тока ротора, силы Лоренца и телесные магнитные силы
Плотность тока. Безразмерное поле плотности тока, для двигателя в базовом корпусе показано на рисунке 1 для стального (а), медного (б) и алюминиевого (в) роторов, соответственно. Токи для стали образуют тонкие шлейфы у поверхности ротора из-за сильного магнитного поля. Проницаемость, которая концентрирует магнитное поле на границе раздела ротор-воздушный зазор ограничение его проникновение в ротор. Распределение тока для медных и алюминиевых роторов очень похоже, учитывая отсутствие намагниченности. Обратите внимание на рис.1, что максимальные значения тока для стали - это самые низкие, в то время как соответствующие для меди самые высокие, как и ожидалось в зависимости от материала ротора электропроводности.
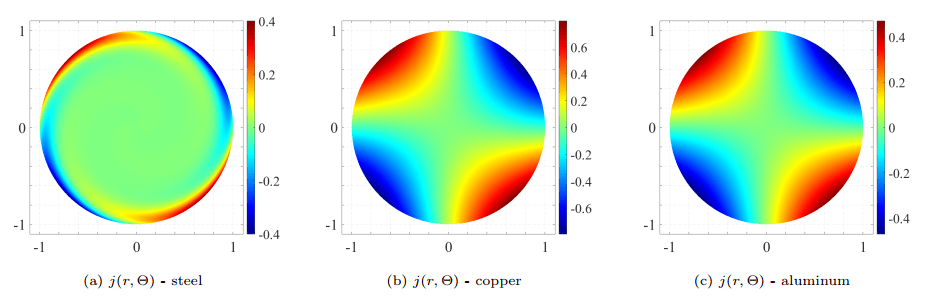
Рисунок 1 – Плотность тока j для двигателя в базовом корпусе: (а) стальной, (б) медный и (в) алюминиевый роторы.
На рисунке 2 показаны амплитуды трех различных составляющих электромагнитной силы (нормированная амплитудой плотности центробежной силы) для базового двигателя со стальным ротором. Первое важное наблюдение состоит в том, что силы Лоренца пренебрежимо малы, а их максимальное значение составляет порядка 1% инерционных сил. Результаты сравнивают силу магнитного тела основного двигателя для различных материалов ротора. Напомним, что сила магнитного тела - это просто сила Лоренца для медные и алюминиевые роторы ввиду их незначительных магнитных свойств. Еще раз подчеркиваем заказы разницы в величине силы магнитного тела между магнитным (стальным) и немагнитным (медь, алюминий) материалы. Силы Лоренца для медного и алюминиевого корпусов ротора сопоставимы, учитывая их близкую электропроводность. Обратите внимание, однако, что хотя максимальная плотность тока выше в меди с лучшей проводимостью, соответствующая максимальная сила Лоренца равна выше для алюминиевого ротора.
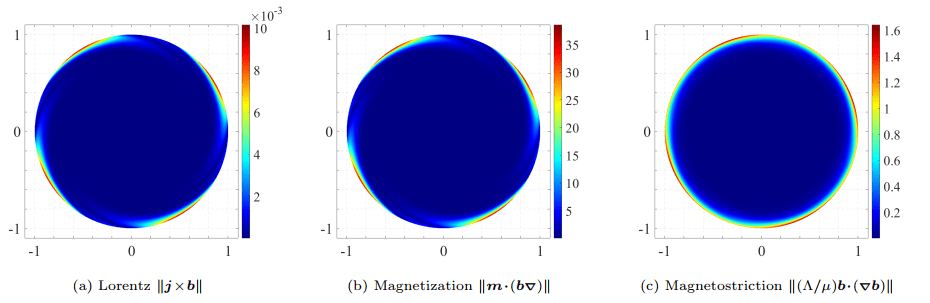
Рисунок 2 – Сравнение различных сил магнитного тела для двигателя в базовом корпусе со стальным ротором.
Обратите внимание, что сила намагничивания больше, чем у ее инерционного аналога (примерно до сорока раз на краю ротора из-за самых высоких градиентов магнитного поля там,указывая на важность учета сил намагничивания в моделях электродвигателей. В магнитострикционные силы не являются незначительными и достигают максимума примерно в 160% от их инерционного аналога (или примерно 5% от максимальных сил намагничивания), несколько неожиданный результат с учетом того же порядка, но объясняются различными выражениями для соответствующих сил.
1.2. Полные и упругие напряжения
Чтобы лучше оценить влияние электромагнитных воздействий на общие и упругие напряжения, предлагаем сравнить их с чисто механическими (только приложенные инерционные телесные силы), плоскими деформационно-упругими решение напряжения для вращающегося ротора двигателя базового случая при угловой скорости, прямой расчет линейной упругости, приводящий к следующему полю напряжений:

Компоненты нормализованного полного напряжения для базового двигателя со стальным ротором представлены на рисунке 3 - с полями напряжений, показанными как в роторе, так и в воздушном зазоре, где можно увидеть непрерывность нормальных составляющих и сдвиговых на границе ротор-воздушный зазор.
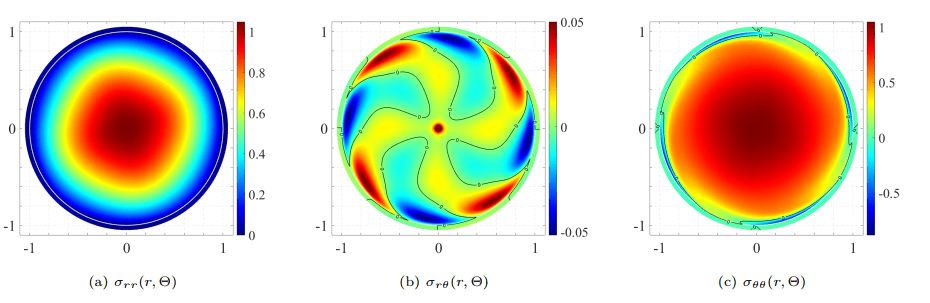
Рисунок 3 – Безразмерные суммарные напряжения в роторе и воздушном зазоре (нормированные на максимальное инерционное напряжение): (а) нормальные, (б) сдвиговые и (c) обруч для стального двигателя базового корпуса.
Общее нормальное напряжение всегда положительно и никогда не превышает максимального, чисто инерционного значения, посколькувидно на рисунке 3(а). Он монотонно увеличивается по мере удаления от края ротора и достигает максимума при центр, область, где электромагнитные эффекты незначительны, в отличие от края ротора. Общая напряжение сдвига изменяется симметрично в пределах примерно ± 5% от максимального (нормального) инерционного напряжения. Также обратите внимание на рисунок 3(б), особенность в r = 0 - усечена на рисунке - из-за приложенного к ней внешнего крутящего момента. Общий обручна пряжения положительно в большей части центральной области, где преобладают инерционные эффекты, с тем же максимумом значение как для чисто инерционного случая. Однако влияние магнитного поля очевидно на ротор край, где действительно появляется сжимающее напряжение того же абсолютного значения, что и максимальное инерционное напряжение.
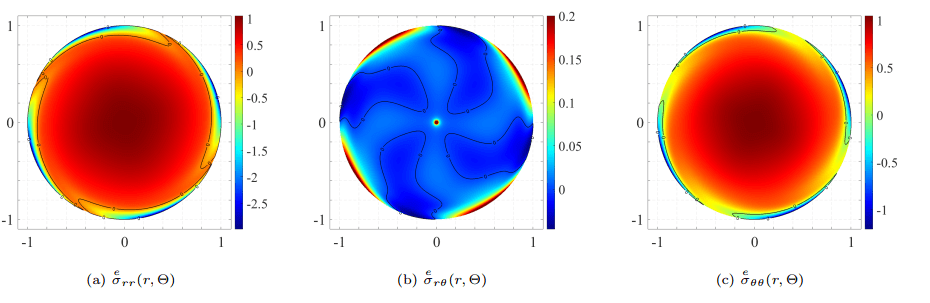
Рисунок 4 – Безразмерные упругие напряжения в роторе (нормированные на максимальное инерционное напряжение): (а) нормальные, (б) сдвиговые и (в) обруч, для стального мотора базового корпуса.
Компоненты нормированного упругого напряжения в роторе приведены на рисунке 4 и существенно различаются от их эквивалентов полного напряжения, как показывает простое сравнение между рисунками 3 и 4. Компоненты упругих напряжений приблизительно равны их инерционным аналогам, заданным формулой 1, из-за слабого магнитныго поля в центре ротора. Однако из-за сильных магнитных полей на границе ротора пограничные слои развиваются около его края, что приводит к сильным сжимающим компонентам, до 250% раз для нормальный и 125% для компонентов обруча, соответственно, выше, чем соответствующий максимальный инерционный стресс. Для компонента напряжения сдвига сравнение между рис.3 (b) и рис. 4 (b) показывает больший упругие напряжения сдвига, в частности вблизи кромки ротора, из-за возникающего механического крутящего момента.
1.3. Крутящий момент ротора
Крутящий момент показан на рисунке 5 как функция коэффициента скольжения. Для низких значений (когда магнитное поле остается ниже уровня насыщения для стали для всех значений скольжения) стальной ротор показывает более высокий крутящий момент, чем его медные и алюминиевые аналоги, почти на весь диапазон скольжения, лишь немного преобладает медный ротор в области скольжения около 5-10%.
Для высоких значений монотонный рост крутящего момента как функция скольжения для стали - из-за ее линейного магнитный отклик - вводит в заблуждение, так как может произойти насыщение, которое не учтено в модели. в базовый двигатель, магнитное поле для стального ротора уже близко к насыщению. В этом случае ожидается, что из-за магнитного насыщения кривая крутящего момента-проскальзывания стали выше s = 2% должна достигать максимального крутящего момента, как в случае с медной и алюминиевые роторы. При s = 5% или выше медный двигатель будет производить больший крутящий момент, чем его стальной аналог.
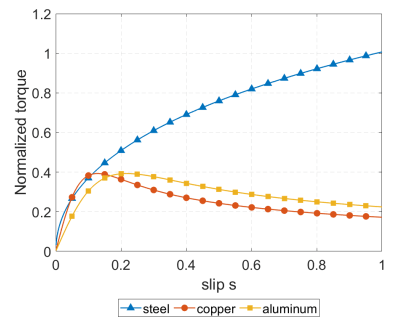
Рисунок 5 – Безразмерный крутящий момент T в зависимости от коэффициента скольжения s для базового двигателя с тремя различные материалы ротора.
Выводы
Используя прямой подход механики сплошной среды, основанный на Kovetz (2000), общую основу, которая сочетает электромагнитные, тепловые и механические эффекты, которые впоследствии применяются для разработки краевая задача для электродвигателей. Особое внимание уделяется выводу связанных материальные уравнения для изотропных материалов при небольшой деформации, но произвольной намагниченности. Как первый приложения, теория используется для аналитического моделирования идеализированного асинхронного двигателя для который мы вычисляем магнитное, тепловое, поля напряжений и его крутящий момент. Чтобы лучше оценить влияние намагничивания от напряжений исследуются три различных материала ротора: электротехническая сталь, медь и алюминий и различные параметры воздушного зазора и скольжения рассматриваются с использованием реалистичного геометрического и рабочего режима значений и материальных параметров. Учитывая линеаризованный магнитная конститутивная модель, принятая для аналитического решения, приложенная амплитуда тока выбрана для создания магнитных полей ниже уровней насыщения.
Результаты магнитного поля показывают, как и ожидалось, наличие пограничного слоя на краю ротора для стальной корпус и более рассеянные рисунки для немагнитных материалов; разница примерно в два порядка наблюдается в максимальном магнитном поле между магнитными и немагнитными материалами. Сравнение Лоренца, намагниченность и магнитострикционные силы в стальном корпусе ротора, мы обнаруживаем, что первые незначительны (более чем на три порядка меньше для первого по сравнению с двумя последними). Более того, магнитострикционные объемные силы возникающие в результате конститутивной связи между напряжением и намагниченностью эффекты - хотя и меньше, чем их магнитные аналоги, но значительно выше, чем у Лоренца. Этот является важным результатом наших расчетов, так как первые обычно не учитываются в электродвигателе. расчеты имеются в литературе. Как и ожидалось, силы магнитного тела в стальном роторе равны сосредоточены вдоль пограничного слоя и значительно выше, чем их аналоги для немагнитных материалы, которые более диффузно распределены, что объясняет важность магнитных роторов для создание гораздо более высокого крутящего момента для данной амплитуды тока, пока сохраняется магнитное поле ниже уровня насыщенности.
Из-за реалистичных тепловых параметров, используемых в расчетах, повышение температуры в роторе составляет пренебрежимо мало, так как максимум температуры появляется в центре ротора. Обнаружены существенные отличия в распределении плотности тока между магнитными и немагнитными материалами, с пограничным слоем проявляющиеся в первом случае, а во втором - диффузные. Аналитическое решение модели позволяет сравнивать различные части тензора напряжений (упругие и общие) к чисто механическим напряжениям из-за инерции, обнаруживая значительное влияние электромагнитные явления на возникающем напряженном состоянии. Хотя максимальное значение общего напряжения нормальное компоненты никогда не превышают своих чисто инерционных аналогов, соответствующие компоненты упругих напряжений Таким образом, путем создания пограничного слоя с концентрацией напряжений, в котором сжимающие радиальные и кольцевые напряжения могут быть до трех раз выше максимального значения инерции. Кроме того, упругие напряжения сдвига значительно увеличиваются выше, чем полное напряжение, и сосредоточено на пограничном слое вокруг кромки ротора.
Несмотря на свои ограничения, предложенная аналитическая модель ясно показывает важность правильного учет связанных магнитомеханических эффектов для точного расчета полей напряжений. В Предложенной методике решения общих краевых задач применима к более сложному двигателю геометрии и нелинейные определяющие реакции, которые включают умеренные деформации, магнитное насыщение и диссипативные эффекты. Для этих задач используется численный подход, основанный на связанных вариационных принципах, необходимо (например, см. Thomas and Triantafyllidis (2009)), а также специальные численные методы для зависимых от времени аспектов проблемы; в этом направлении планируются дальнейшие исследования.
Список использованной литературы
1. Abdel-Razek, A., Coulomb, J., Feliachi, M., Sabonnadiere, J., 1982. Conception of an air-gap element for the dynamic analysis of the electromagnetic field in electric machines. IEEE Transactions on Magnetics 18, 655-659.
2. Arkkio, A., 1987. Analysis of induction motors based on the numerical solution of the magnetic field and circuit equations, 97
3. Aydin, U., Rasilo, P., Martin, F., Singh, D., Daniel, L., Belahcen, A., Rekik, M., Hubert, O., Kouhia, R., Arkkio, A.,
2017. Magneto-mechanical modeling of electrical steel sheets. Journal of Magnetism and Magnetic Materials 439, 82-90.
4. Barber, J., 2009. Elasticity. Solid Mechanics and Its Applications, Springer Netherlands.
5. Belahcen, A., Fonteyn, K., Fortino, S., Kouhia, R., 2006. A coupled magnetoelastic model for ferromagnetic materials. Proc. of the IX Finnish Mechanics Days. von Hertzen R., Halme T.(eds.) , 673-682.
6. Boules, N., 1984. Two-dimensional field analysis of cylindrical machines with permanent magnet excitation. IEEE Transactions on Industry Applications IA-20, 1267-1277.
7. Chari, M.V.K., Silvester, P., 1971. Analysis of turboalternator magnetic fields by finite elements. IEEE Transactions on Power Apparatus and Systems PAS-90, 454-464.
8. Coleman, B.D., Noll, W., 1963. The thermodynamics of elastic materials with heat conduction and viscosity. Archive for
Rational Mechanics and Analysis 13, 167-178.
9. Daniel, L., Hubert, O., 2009. An analytical model for the ?e effect in magnetic materials. The European Physical Journal Applied Physics 45, 31101.
10. DDevillers, E., Le Besnerais, J., Lubin, T., Hecquet, M., Lecointe, J., 2016. A review of subdomain modeling techniques in electrical machines: Performances and applications, in: 2016 XXII International Conference on Electrical Machines (ICEM),pp. 86-92.
11. Fonteyn, K., Belahcen, A., Kouhia, R., Rasilo, P., Arkkio, A., 2010a. Fem for directly coupled magneto-mechanical phenomena in electrical machines. IEEE Transactions on Magnetics 46, 2923-2926.
12. Gieras, J.F., Saari, J., 2012. Performance calculation for a high-speed solid-rotor induction motor. IEEE Transactions on Industrial Electronics 59, 2689-2700.
13. Hiptmair, R., Ostrowski, J., 2005. Coupled boundary-element scheme for eddy-current computation. Journal of Engineering Mathematics 51, 231-250.
14. Hutter, K., Ven, A.A., Ursescu, A., 2007. Electromagnetic Field Matter Interactions in Thermoelasic Solids and Viscous Fluids.volume 710. Springer.
15. Kankanala, S., Triantafyllidis, N., 2004. On finitely strained magnetorheological elastomers. Journal of the Mechanics and Physics of Solids 52, 2869-2908.
16. Lubin, T., Mezani, S., Rezzoug, A., 2011. Analytic calculation of eddy currents in the slots of electrical machines: Application to cage rotor induction motors. IEEE Transactions on Magnetics 47, 4650-4659.
17. Pao, Y.H., Yeh, C.S., 1973. A linear theory for soft ferromagnetic elastic solids. International Journal of Engineering Science 11, 415-436.
18. Reyne, G., Sabonnadiere, J., Coulomb, J., Brissonneau, P., 1987. A survey of the main aspects of magnetic forces and
mechanical behaviour of ferromagnetic materials under magnetisation. IEEE Transactions on Magnetics 23, 3765-3767.
19. Reyne, G., Sabonnadiere, J.C., Imhoff, J.F., 1988. Finite element modelling of electromagnetic force densities in dc machines. IEEE Transactions on Magnetics 24, 3171-3173.
20. Zhu, Z.Q., Howe, D., Bolte, E., Ackermann, B., 1993. Instantaneous magnetic field distribution in brushless permanent
magnet dc motors. i. open-circuit field. IEEE Transactions on Magnetics 29, 124-135.