Аннотация
Рассматривается методика оптимального проектирования тяжелых козловых кранов модифицированным методом Хука-Дживса, принципа Парето, безразмерных параметров.
Введение
При общей детальной разработке вопросов оптимального проектирования металлоконструкции и механизмов грузоподъёмных машин актуальной проблемой остаётся оптимальное проектирование специальных кранов и особенно сложных козловых кранов и уникальных конструкций специальных козловых кранов для монтажных работ, судостроительных козловых кранов. Их отличают сложность конструкции, большая металлоёмкость, высокие классы ответственности, отказ в работе которых может привести к травмированию и даже гибели людей, большие экономические потери
Сложность их расчета и проектирования заключается в малосерийном, единичном производстве таких машин. Это усложняет сбор статистических данных по особенностям эксплуатации, надёжности и безотказности этих машин. В целом оптимальное проектирование включает параметрическую и структурную оптимизацию металлоконструкции и механизмов. Параметрическая оптимизация включает набор сечения элементов металлоконструкции по выбранному критерию оптимизации. В качестве критерия на первом этапе обычно выбирается металлоёмкость, от которой зависит энергоёмкость механизмов передвижения крана и крановых тележек.
На этом этапе применима модификация метода Хука-Дживса [1]. Классический метод Хука-Дживса позволяет оптимизировать овражные функции
, направление движения к экстремуму целевой функции, в которых меняется в процессе исследования.
Однако указанный метод разработан для задач безусловной оптимизации, а большинство инженерных задач требуют выполнения ряда условий. В краностроениеи это условия прочности, устойчивости, статической и динамической жёсткости металлоконструкций. Кроме того, он применим лишь для неразрывных функций. При исследовании оптимальности по металлоёмкости разрывом функции будет невыполнение одного из указанных условий. Было предложено применять метод Хука-Дживса в основной программе, а все ограничения проверять в подпрограммах. В
основной программе рассматриваются только варианты, удовлетворяющие всех ограничениям. В указанной модификации предложено также отказаться от движения по образцу
с изменением сразу всех параметров в направлении экстремума функции. Вместо движения по образцу производится движение только в направлении одного фактора, позволяющего получить наибольшее или наименьшее значение целевой функции. Это возможно при небольшом числе исследуемых факторов. В исследовании коробчатых металлоконструкций предложено варьирование высотой
или шириной балки с подбором толщин используемого листового металла по условиям ограничений.
В литературе предложено много способов поиска минимума поперечных сечений коробчатых балок, дающих приблизительно одинаковые результаты по оптимальности. Больший эффект по металлоёмкости даёт структурная оптимизация, позволяющая менять саму структурную схему металлоконструкции кранов. Существует большое число конструктивных схем, выбрать наилучшую можно только при сравнении всех схем для заданных исходных параметров, причем сравнение схем необходимо проводить после определения минимума металлоёмкости методами параметрической оптимизации.
Предложенный метод структурной оптимизации позволяет конструировать новые схемы с добавлением или удалением «лишних» элементов пространственных рамных конструкций, каковыми являются рассматриваемые краны. Для решения таких задач более применим метод граничных элементов в отличие от хорошо разработанного метода конечных элементов [2]. Метод граничных элементов позволяет сразу найти точку экстремума аналитическими методами в отличие от дискретного метода конечных элементов. При этом значительно снижаются размеры матриц, что позволяет использовать вычислительные машины меньшего объёма памяти.
В последние годы для решения оптимизационных задач проектирования специальных кранов предложены методы многокритериальной оптимизации на основании принципа Парето [3]. Долгое время считалось, что если критерий оптимальности должен быть единственным, то на основании указанного принципа критерий может быть многокритериальным. Например, для металлоконструкций всегда требовалось получение не только минимума металлоёмкости, но и стоимости, удобства эксплуатации, морозостойкости, других критериев. Особенно детально принцип Парето разработан для проектирования планетарных редукторов, которые широко применяются для кранов атомных электростанций, многоскоростных механизмов монтажных кранов.
Для исследования оптимальных параметров механизмов кранов предложены безразмерные критерии [1]. По данной методике выбирается первый вариант механизма, который принимается за базовый. Все остальные варианты исследуются по безразмерному критерию. Для механизма передвижения, например, это выглядит так
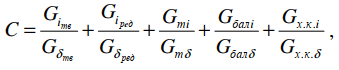
где С – безразмерный критерий оптимизации;
Gi , Giред , Giт , Gбал.i , Gх.к.i – текущее значение масс двигателя, редуктора, тормоза, балансиров, ходовых колёс;
Gδ двиг., Gδред , Gδт , Gбал.δ , Gх.к.δ – массы двигателя, редукторов, тормоза, балансиров, ходовых колёс базового варианта.
Известно, что с изменением диаметра ходового колеса меняется вся структура комплектующих механизмов. Оптимальным будет вариант, дающий наименьшее значение безразмерного критерия С.
Аналогично исследуются механизмы подъёма груза, только варианты комплектации выбираются по назначаемой кратности полиспаста. От его значения изменяются параметры двигателя, редуктора, барабана, каната, тормозов. В последние два года научный коллектив лаборатории Машиноведение и ПТМ
занимается разработкой методов оптимального автоматизированного проектирования механизмов и металлоконструкции кранов (рисунок 1).
На рисунке 1 показана схема автоматизированного выбора параметров механизмов передвижения кранов и крановых тележек. Для этого в память машины вводятся исходные данные параметров и аналитические зависимости выбора параметров механизма в виде ограничений и двумерные массивы базы данных комплектующих элементов. Далее перебором строк и столбцов На рисунке показана схема автоматизированного выбора параметров механизмов передвижения кранов и крановых тележек. Для этого в память машины вводятся исходные данные параметров и аналитические зависимости выбора параметров механизма в виде ограничений и двумерные массивы базы данных комплектующих элементов. Далее перебором строк и столбцов

Рисунок 1 – Схема автоматизированного выбора параметров механизмов передвижения
Список использованной литературы
- Кобзев А. П. Оптимальное проектирование тяжёлых козловых кранов / А. П. Кобзев. Саратов: Изд.СГТУ, 1991. 157 с.
- Барановская Л. В. Оптимальное проектирование тяжёлых козловых кранов с использованием метода граничных элементов / Л. В. Барановская, А. П. Кобзев. Саратов: Вестник СГТУ. 2009. №2(38) С. 56-61.
- Чернова Н. М. Метод оптимального проектирования механизмов передвижения кранов на основе принципа Парето / Н. М. Чернова, А. П. Кобзев // Известия ТулГУ. 2009. Вып.2.