Искусственный интеллект при классификации неисправностей с высоким сопротивлением в системе распределения электроэнергии
Автор: Santosh Ramana Kumar Joga
Автор перевода: В. Г. Беззуб
Источник: International Conference on Recent Trends in Computing, Communication and Networking Technologies (ICRTCCNT’19), Kings Engineering College, October 18-19, 2019, Chennai, Tamilnadu, India.
Аннотация. Даная работа исследует различные типы классификаторов на основе искусственного интеллекта для классификации неисправностей. Метод извлечения признаков, предложенный на основе новой концепции, основанной на двойном трехволновом преобразовании, объединенным с нейронной сетью. В последние дни обнаружение неисправности с высоким сопротивлением стало самой сложной задачей для инженеров-электриков. Повреждения с высоким сопротивлением (ПВС) не идентифицируются обычной системой защиты от перегрузки по току, такой, как схема релейной защиты от перегрузки по току, из-за ее уникальности по величине тока короткого замыкания, природе и характеристикам. В этой статье переходной сигнал анализируется с использованием метода на двойном трехволновом преобразовании метод извлечения признаков, коэффициенты извлекаются по шкале 3. В этой статье ПВС,L-G, L-L-G классифицируются с помощью классификаторов на основе нейронных сетей. Метод применяется к стандартной радиальной распределительной сети типа IEEE33 и работа моделирования в среде MATLAB приводит к необходимым результатам.
Ключевые слова — повреждения высокого сопротивления, волновой, нейронная сеть, классификация неисправностей, обнаружение неисправностей, КВПДД.
I. ВВЕДЕНИЕ
Возможность возникновения неисправности в системе распределения электроэнергии встречается чаще. Электрическая неисправность - это ненормальное состояние, вызванное отказом оборудования в энергосистеме, ненадлежащими погодными условиями и ошибками человека. Эти неисправности вызывают повреждение оборудования и человеческие потери, зависят от их серьезности. Всякий раз, когда происходит сбой, номинальные значения напряжения и тока отклоняются, что вызывает чрезмерно высокий или низкий ток в распределительной системе, что приводит к повреждению оборудования и человеческим жертвам. Обнаружение неисправности должно выполняться немедленно, чтобы уменьшить отключение электроэнергии. В системе распределения электроэнергии может произойти много неисправностей, таких как L-G, L-L неисправность и с высоким сопротивлением, раннее обнаружение неисправности сохраняет надежность энергосистемы, а также снижает потери людей и имущества. Эти сбои с высоким сопротивлением трудно обнаружить с помощью обычных реле максимального тока. ПВС возникает, когда электрический проводник вступает в электрический контакт с поверхностью земли или с предметом, который сопротивляется прохождению тока короткого замыкания до уровня ниже чем уровень надежности, обнаруживаемого обычными системами защиты от перегрузки по току. В настоящее время исследователи работаю над обнаружением повреждений с высоким сопротивлением для повышения надежности системы распределения электроэнергии. Для анализа переходного сигнала на основе волны обычно используется метод извлечения признаков. В этой работе трехволновое преобразование используется для выделения признаков и анализа переходного сигнала.
А. Типы неисправностей
Неисправности подразделяются на две группы: неисправность обрыва цепи и неисправность короткого замыкания, неисправности короткого замыкания, далее классифицируемые на симметричные и несимметричные неисправности. В то время как короткое замыкание между проводом на землю L-G и двойным замыканием на землю L-L-G относится к несимметричным замыканиям, то, когда один провод встречается с землей или с нулевым проводом, как показано на рис. 1., возникает замыкание L-G. Вероятность возникновения этих неисправностей составляет почти 70-80%, когда две линии сходятся друг с другом и падают на землю, как показано на рис. 1.б возникает неисправность L-L-G. Вероятность возникновения этих неисправностей составляет почти 10%.
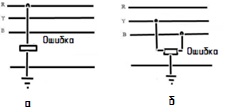
Рисунок 1.a – Ошибка L-G Рисунок 1.б – Ошибка L-L-G
A. Повреждения с высоким сопротивлением (ПВС)
Многие исследователи работают над моделированием высокоомных коротких замыканий и пришли к выводу, что ПВС являются нелинейными и асимметричными. Эмануэль разработал модель ПВС - это модель, основанная на практических измерениях и теоретических компонентах, представленных в виде двух источников постоянного тока, соединенных антипараллельно с двумя диодами для создания нулевых периодов дуги и асимметрии. На рис.1.в для учета нелинейности [8][9] при моделировании замыкания на землю с использованием сопротивления заземления он использовал источник постоянного тока, пару диодов, размещенных антипараллельно, и сопротивления с разными значениями.
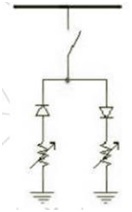
Рисунок 1.в – Модель ПВС Эммануэля
Модель Эммануэля дополнительно упрощена в [3] [4]. Эти неравные сопротивления представляют собой асимметричные токи короткого замыкания которые протекают в системе. Сопротивления короткому замыканию представлены как Rp и Rn. Неравные значения для этих двух сопротивлений позволяют создавать асимметричные токи короткого замыкания. Упрощенная модель ПВС показана на рис.1.г, и она моделируется в MATLAB Simulink для дальнейшего процесса классификации неисправностей.

Рисунок 1.г – модифицированная модель ПВС Эммануэля
II. КОМПЛЕКСНОЕ ВОЛНОВОЕ ПРЕОБРАЗОВАНИЕ ДВОЙНОГО ДЕРЕВА
Комплексное волновое-преобразование двойного дерева (КВ-ПДД)[1],[7],[6],[5] - метод извлечения признаков с некоторыми важными дополнительными свойствами, добавленными к обычному волновому-преобразованию, он был впервые представлен профессором Кембриджского университета Ником Кингсбери в 1998 году. Комплексное волновое преобразование с двойным деревом состоит из двух волновых-деревьев; п ервое волновое-дерево дает действительную часть преобразования, а вторичная часть дает мнимую часть, как показано на рисунке 2.a в отличие от дискретного волнового-преобразования, двойное древовидное волновое-преобразование требует новых фильтров на начальных этапах, первоначально пара наборов фильтров, выбранных так, чтобы соответствующие волны из приближенной пары преобразования Гильберта, это требует, чтобы два реальных вейвлет-преобразования использовали два разных набора фильтров, каждый из которых удовлетворяет условиям PR. Два набора фильтров разработаны совместно, так что общее преобразование является приблизительно аналитическим.

Рисунок 2.а – Блок-схема для 3-х уровневого КВПДД
Преимущества КВПДД над КДД:
- Инвариантность сдвига является приблизительной, и изменения во временном сдвиге обновляются лучше по сравнению с дискретным волновым-преобразованием. Хорошая направленная селективность (дискретное волновое-преобразование дает селективность функции только в 3 направлениях с плохой селективностью, в отличие от двойного древовидного волнового, комплексное преобразование, которого имеет 12 направлений.
- Информация о фазе доступна.
- Идеальная реконструкция (ИР) будет достигнута с использованием коротких линейно-фазовых фильтров по сравнению с дискретным волновым-преобразованием.
- Резервирование ограничено, независимо от количества шкал.
- Вычисления могут выполняться до n порядков.
- Производительность не зависит от главной волны.
III. ВИДЫ КЛАССИФИКАТОРОВ
A. Вероятностная нейронная сеть (ВНС)
Вероятностная нейронная сеть - это 4-х слойная нейронная сеть, которая в основном используется для задач классификации и регрессии. В этом типе классификатора группа точек данных будет назначена каждому классу, основная функция - классифицировать любые новые данные в один из классов. Вероятностная нейронная сеть также используется в качестве мультиклассового классификатора. Он состоит из четырех слоев, как показано на рис.3.а.
- Входной слой: - Входной слой состоит из нейронов с набором измерений. Точки данных подаются на входной слой, который позже этим входным нейронам подаются значениями данных каждого нейрона в скрытом слое.
- Слой модели: этот слой модели является скрытым слоем, состоящим из функций Гаусса. В этом слое скрытые нейроны вычисляют евклидово расстояние каждого тестового примера от центральной точки нейронов и применяют радиальные базовые функции, в основном функции ядра, используя значения сигмы.
- Слой суммирования: - Произойдет необходимое суммирование нейронов, поступающих из слоя шаблона, в соответствии с этим суммированием предсказанные выходные данные будут отправлены на выходной слой.
- Выходной слой: - Выходной слой, на который подается слой шаблона, теперь выбирает наибольшее значение из данных, предоставленных слоем шаблона, выполняя эту задачу, он разделяет данные по классам.
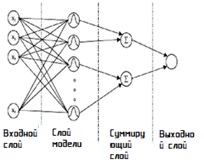
Рисунок 3.а – Блок-схема вероятностной нейронной сети
Б. Нейронная сеть обратного распространения (НСОР)
Нейронная сеть обратного распространения [1] - это алгоритм обучения с учителем для обучения многослойных перцептронов. Он состоит из цели, в которой вычисляется ошибка для обновления весов, чтобы минимизировать ошибку. Как только ошибка сведена к минимуму, для заданных входных данных создается требуемый вывод. Блок-схема нейронной сети обратного распространения [2], как показано на рис.3.б состоит из n слоев, но здесь мы рассматриваем только трехслойные нейронные сети.

Рис.3.б – Блок-схема нейронной сети обратного распространения
IV. ПРЕДЛАГАЕМАЯ РАБОТА
В предлагаемой работе IEEE33 Bus Standard используется радиальная распределительная сеть, система рассматривается без генерации распределения, размещенной на слабых шинах. А Генератор 12,6 кВ используется для питания системы и каждой шины, расположенной на 50 км. Блок-схема радиальной распределительной сети с шиной IEEE33 показана на рис.4.а. Тестовые данные, такие как данные шины и данные нагрузки, взяты в соответствии со стандартом.
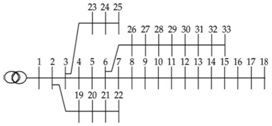
Рисунок 4.a – Блок-схема радиальной распределительной сети IEEE33
Модель MATLAB Simulink разработана для моделирования и проверки поведения напряжения и тока на каждой шине с помощью алгоритма Backward Forward Sweep , и слабые шины идентифицируются, и это показано на рис.4.б.
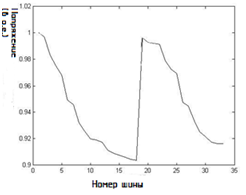
Рисунок 4.б – Напряжение на каждой шине в IEEE33 RDN
Переходный сигнал исследуется таким образом, чтобы выявить различные типы повреждений, например, замыкание с высоким сопротивлением, замыкание линии на землю и двойное падение линии на землю происходит для каждой шины и характеристики сигнала тока извлекаются на каждой шине с учетом точки измерения на генераторе. Извлечение признаков выполняется с помощью комплексного преобразования двойного древовидной волны. Блок-схема всей предлагаемой работы представлена на рис.4.в.
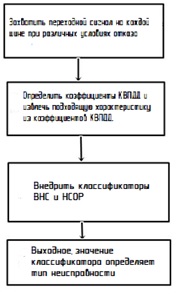
Рисунок 4.в – Блок-схема предлагаемой работы
Коэффициенты КВПДД уровня 3 определяются на каждой шине при различных условиях неисправности. Коэффициенты КВПДД на шине № 6 для неисправности с высоким сопротивлением, неисправности L-G и неисправности L-L-G сформулированы в таблице 1.
| ПВС | L-G | L-L-G |
| 4.7500 | 2.0200 | 0.9500 |
| 3.2800 | 8.9000 | 0.7211 |
| 1.3170 | 1.8000 | 0.7500 |
| 1.0190 | 1.5250 | 0.7211 |
| 0.4000 | 7.5300 | 0.6002 |
| 2.2450 | 3.6060 | 0.1984 |
| 6.0130 | 3.0109 | 0.2744 |
| 5.3850 | 4.4720 | 0.2002 |
| 4.0610 | 3.4890 | 0.1658 |
| 0.1100 | 1.0103 | 0.1385 |
| 0.4200 | 2.6180 | 0.3601 |
| 3.8840 | 4.0000 | 0.6541 |
| 1.7190 | 0.1890 | 0.1830 |
| 2.4350 | 9.9040 | 0.2456 |
| 3.8745 | 4.1267 | 0.1178 |
| 0.4670 | 1.1135 | 0.6890 |
Теперь выбранные подходящие характеристики из коэффициентов КВПДД, взятых с каждой шины при каждой отдельной неисправности, вводятся в искусственную нейронную сеть на основе классификаторов для классификации типа неисправности данного переходного сигнала. Код MATLAB разработан для классификации типа неисправности переходного сигнала для классификатора типа вероятностной нейронной сети и классификатора типа нейронной сети обратного распространения. Обобщенный алгоритм классификатора ВНС приведен ниже.
- инициализовать обучение;
- загрузить данные;
- загрузить классификации;
- написать программу цикла для установки классов на заданные данные;
- подача данных на входные нейроны;
- установить цели;
- принять значение спреда как 1;
- посчитать значение сети;
- рассчитать выходное значение;
- установить traingdx как функцию обучения нейронной сети;
- установить mse как функцию производительности нейронной сети;
- построить график производительности, состояния тренировки, регрессии, соответствия и истории;
- обучить сетевые данные по назначенным классам;
- назначить нейронную сеть функцию разделения дивиденда;
- назначить коэффициент обучения, коэффициент тестирования и коэффициент ценности;
- Инструмент обучения ВНС предназначается для обучения данных;
- рассчитать результат и ошибки;
- обновить веса с учетом изменения ошибки;
- график производительности, состояние обучения;
- построить матрицу беспорядка из целей и результатов.
С помощью вышеуказанного алгоритма кода MATLAB для классификатора ВНС обучаются входные данные, которые являются коэффициентом КВПДД на уровне 3 каждой шины при каждой отдельной неисправности. Всего рассматривается 671 выборка из всех выборок данных, извлеченных с помощью комплексного волнового-преобразования двойного дерева из переходных сигналов. Инструмент вероятностного обучения нейронной сети показан на рис.4.г.

Рисунок 4.г – Инструмент обучения ВНС
traingdx [10] - это функция обучения сети, используемая для обучения данных. В предлагаемой работе в качестве функции производительности сети используется метод среднеквадратичной ошибки. Показатель среднеквадратичной ошибки (mse) [11] является одной из функций производительности сети; он измеряет производительность сети согласно среднему квадрату ошибок. Функция разделения сети, используемая при обучении нейронной сети, является делимой [12]. Она разделяет цели на три набора: обучение, проверка и тестирование с использованием случайных индексов. Аналогичным образом разработан код MATLAB для классификации типа неисправности переходного сигнала для классификатора типов нейронной сети обратного распространения. ' Всего 671 выборка выбрана из коэффициентов КВПДД, извлеченных на каждой шине, и различных неисправностей с учетом точки измерения в генераторе. Обучающий инструмент нейронной сети обратного распространения показан на рис. 4.д.
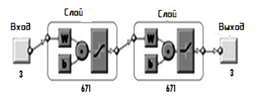
Рисунок 4.д – Инструмент обучения нейронной сети обратного распространения
V. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Выполнение предложенной работы анализируется путем анализа матрицы беспорядка, полученной при обучении входных данных в классификаторе вероятностных нейронных сетей и классификаторах нейронных сетей обратного распространения. Матрица беспорядка, полученная при обучении входных данных в классификаторе типа ВНС, представлена в таблице 2.
| Повреждения с высоким сопротивлением | Ошибка L-G | Ошибка L-L-G | % | |
| Повреждения с высоким сопротивлением | 509 | 3 | 0 | 99.41 |
| Ошибка L-G | 0 | 64 | 1 | 98.46 |
| Ошибка L-L-G | 0 | 64 | 1 | 98.46 |
| 98.8 |
На основе матрицы неточностей неисправности с высоким сопротивлением классифицируются с точностью 99,41%, где в 509 выборках предсказан результат ДА, а в 3 выборах предсказан результат НЕТ, из-за неисправности повреждения с высоким сопротивлением. Принимая во внимание, что из 65 выборок ошибки L-G всего в 64 образцах предсказан результат ДА, а в 1 образце – прогнозирован с результатом «НЕТ» с точностью 98,46%. Точно так же из 97 образцов ошибки L-L-G всего 93 образца предсказаны с результатом ДА, а в 4 образцах предсказан результат «НЕТ» с точностью 95,87%. Общая точность обучения классификатора типа «Вероятностная нейронная сеть» составляет 98,8%. Матрица беспорядка, полученная при обучении входных данных нейронной сетью обратного распространения, показана в таблице 3.
| Повреждения с высоким сопротивлением | Ошибка L-G | Ошибка L-L-G | % | |
| Повреждения с высоким сопротивлением | 500 | 5 | 7 | 97.65 |
| Ошибка L-G | 0 | 63 | 2 | 96.92 |
| Ошибка L-L-G | 0 | 5 | 1 | 92 |
| 97.61 |
На основе матрицы беспорядка неисправности с высоким сопротивлением классифицируются с точностью 97,65%, при этом в 500 выборках предсказывают результат ДА, а в 12 выборках – НЕТ, поскольку ошибка является неисправностью с высоким сопротивлением. Принимая во внимание, что из 65 выборок ошибки L-G 63 выборки являются прогнозируемыми с результатом ДА, а 2 выборки - прогнозируемыми НЕТ с точностью 96,92%. Аналогичным образом из 97 выборок ошибки L-L-G 92 выборки предсказаны с результатом ДА, а 5 выборкам предсказан результат НЕТ с точностью 94,84%. Общая точность обучения классификатора типа вероятностной нейронной сети составляет 97,61%. Путем сравнения матрицы беспорядка классификатора типа вероятностной нейронной сети Табл.2 и классификатора типа нейронной сети обратного распространения из Табл.3. Классификатор хорошо работает с точностью 99,41% при классификации короткого замыкания с высоким сопротивлении по сравнению с классификатором с обратным распространением. Стоит отметить, что неполадки L-G и L-L-G эффективно классифицируются с помощью классификаторов вероятностного типа нейронной сети по сравнению с классификатором с обратным распространением. В этой статье обнаруживается только неисправность с высоким сопротивлением, которая классифицируется с другими неисправностями, возникающими в системе распределения электроэнергии. Используя методы искусственного интеллекта и машинного обучения, мы можем даже обнаружить неисправность с высоким сопротивлением в системе распределения электроэнергии с помощью метода извлечения признаков на основе КВПДД. Дальнейшие исследования проводятся для определения места неисправности.
Сравнительная таблица представлена в таблице 4.
| Тип ошибки Тип классификатора |
ПВС | L-G | L-L-G |
| ВНС |
99.41% | 98.46% | 95.87% |
| НСОР | 97.65% | 96.92% | 94.84% |
Перечень ссылок
[1] Soumi chakraborty, Amitava Chatterjee, and Swapam kumar goswami, A dual tree complex wavelet transform based approach for recognition of power system transients
, 2014 wiley publishing ltd Experts system, vol.32 No.1, pp. 132–140, Febuary 2015.
[2] serigo silva, Pyramo Costaa, Maury Gouveaa, Alcyr Lacerdaa, Franciele Alvesa,”High impedance fault detection in power distribution systems using wavelet transform and evolving neural network ”, Electric Power Systems Research 154 (2018), pp.474–483.
[3] Shyam Salona,” High Impedance Fault Modelling on 11Kv Feeder Using Matlab Simulink”,International Journal of Science and Research (IJSR) Volume 5 Issue 5, May 2016,pp. 462-467.
[4] Naser Zamanan, Jan Sykulski The Evolution of High Impedance Fault Modeling
, 2014 IEEE,pp.77-81.
[5] Abhimanyu Panwar, Rohin Bisht, Prashant Jha, Power Quality Analysis using Dual Tree Complex Wavelet Transform
, 2012 Students Conference on Engineering and Systems
[6] B.K. Panigrahi, Senior Member, IEEE, Anant Baijal, Krishna Chaitanya P. and Preetam P. Nayak, Power Quality Analysis using Complex Wavelet Transform
, 2010 Joint International Conference on Power Electronics, Drives and Energy Systems & 2010 Power India
[7] Ivan W. Selesnick, Richard G. Baraniuk, and Nick G. Kingsbury,The Dual-Tree Complex Wavelet Transform
IEEE SIGNAL PROCESSING MAGAZINE, NOVEMBER 2005,pp.123- 151.
[8] Marek Michalik, Waldemar Rebizant, Member, IEEE, Miroslaw Lukowicz, Seung-Jae Lee, Member, IEEE, and Sang-Hee Kang, Member, IEEE,High-Impedance Fault Detection in Distribution Networks With Use of Wavelet-Based Algorithm
, IEEE TRANSACTIONS ON POWER DELIVERY, VOL. 21, NO. 4, OCTOBER 2006,pp.1793-1802.
[9] Chul-Hwan Kim, Member, IEEE, Hyun Kim, Young-Hun Ko, Sung- Hyun Byun,Raj K. Aggarwal, Senior Member, IEEE, and Allan T. Johns, Senior Member, IEEE, A Novel Fault-Detection Technique of High-Impedance Arcing Faults in Transmission Lines Using the Wavelet Transform
, IEEE TRANSACTIONS ON POWER DELIVERY, VOL. 17, NO. 4, OCTOBER 2002,pp.921-929.
[10] mathwork,https://in.mathworks.com/help/deeplearning/ref/traingdx.html
[11] mathwork,https://in.mathworks.com/help/deeplearning/ref/mse.html
[12] mathwork,https://in.mathworks.com/help/deeplearning/ref/dividerand.html