Аннотация
Энергетические аспекты являются основополагающими при проектировании систем электропривода. В данной статье описываются энергетические характеристики асинхронных электроприводов, основанные на различных методах управления. Сравнение этих электроприводов показывает, что векторные методы управления имеют значительное преимущество перед скалярными методами управления. Математическое описание асинхронного электропривода основано на теории векторного управления и методе главных компонент. Уравнения, полученные путем математического описания, позволяют рассчитывать токи, напряжения и электрическую мощность на выходе, когда электромагнитный крутящий момент и скорость машины установлены. Энергетические характеристики асинхронного привода были получены с использованием программы моделирования MATLAB–SIMULINK.
Ключевые слова: энергетические характеристики, асинхронный электропривод, скалярные методы управления, векторные методы управления
Введение
Для силовых промышленных приводов существенными являются не только динамические, но и в основном энергетические характеристики. Энергетические характеристики замкнутого асинхронного электропривода, а также динамические характеристики зависят от его структуры, выбранных законов и способов управления. Анализ проблемы показывает, что в современных энергосистемах все еще существуют неиспользованные резервы повышения энергоэффективности при преобразовании электромеханической энергии. Наибольший потенциал повышения эффективности электромеханического преобразования энергии может быть получен при оптимизации режимов работы системы.
В данной статье представлен расчет и сравнение энергетических показателей асинхронного электропривода для различных законов и способов управления. Асинхронная машина с короткозамкнутым ротором (АМСКР) является значимым нелинейным объектом управления. Построение электропривода с АМСКР требует структурно–параметрического синтеза.
Выбор метода управления АМСКР является первым этапом структурного синтеза.
Согласно анализу метода управления весь привод короткозамкнутой машины можно разделить на два широких класса управления:
- Скалярный метод управления.
- Векторный метод управления.
Реализация скалярных методов управления осуществляется с использованием нелинейных регуляторов.
Эти регуляторы обеспечивают нелинейную зависимость между напряжением (током) и частотой на выходе инвертора. Для скалярного метода управления нет строгих требований к динамическому процессу. Реализация метода векторного управления осуществляется путем фазового регулирования напряжения или тока на выходе инвертора. Основой построения асинхронных электроприводов с векторным управлением служит метод структурного синтеза. Этот метод описан в работе Бойчук. Дальнейшее развитие этого метода было осуществлено в работа О. С. Попова по решению обратных динамических задач.
МЕТОДОЛОГИЯ ИССЛЕДОВАНИЯ
Основным условием структурного синтеза асинхронного электропривода является выбор базового вектора. Выбор базового вектора определяет связь между электромагнитными переменными АМСКР и угловой частотой (координатной скоростью вращения). В представлены шесть основных структур асинхронного электропривода, которые обозначены в соответствии с выбранным базовым вектором как:
- Базовый вектор–это напряжение статора Us
- Базовый вектор напряжения ротора Ur
- Базовый вектор–это ток статора Is
- Базовый вектор тока ротора Ir
- Базовый вектор потока статора ψs
- Базовый вектор–это поток Ротора ψr
В асинхронных векторных системах крутящий момент определяется как произведение пар пространственных векторов.
Уравнения крутящего момента для всех векторных комбинаций представлены в монографии.
Приведем уравнения крутящего момента только для двух комбинаций векторов, которые наиболее распространены в асинхронном электроприводе. Первое из этих уравнений соответствует системе с базовым вектором магнитного потока Ротора (FOC–Field Oriented Control). Второе из этих уравнений соответствует прямому управлению крутящим моментом (DTC–Direct Управление Крутящим Моментом).
Для мощных асинхронных электроприводов необходимы не только динамические свойства, но и энергетические характеристики. Рассчитаны энергетические характеристики асинхронных электроприводов в статических режимах работы. В данной статье проводится оценка при задании крутящего момента и частоты вращения на валу асинхронного двигателя в замкнутом контуре электропривода.
РАСЧЕТ И МОДЕЛИРОВАНИЕ
Исследование энергетических характеристик асинхронного электропривода с полевым управлением Исследование энергетических характеристик асинхронного электропривода с базовым вектором магнитного потока Ротора (FOC–field oriented control), реализованного для асинхронной машины мощностью 15 кВт со следующими паспортными данными и параметрами:Номинальная мощность–Sn(Ва), среднеквадратичное напряжение (линия–линия) – Un (Vrms), частота–fn(Гц):
Sn = 1.845e + 04 (Va), Un = 400V, (U1m = 310V), fn = 50 Hz, (ω = 3141/S).
Сопротивление статора и индуктивность Rs (ом) Ls (H):
Rs = 0.2147Ω, Ls = 0.06518H.
Сопротивление ротора и индуктивность (RR (ом) LR(H)):
RR = 0.2205Ω, LR = 0.06518 H. Взаимная индуктивность Lm (H): Lm 0.06419 H. Инерция, пары полюсов: J = 0.102 Кг/м2,ρ = 2.
В основе математического описания асинхронного электропривода лежит метод базового вектора и метод главных компонент. Математическое описание электропривода в статическом режиме базовый вектор магнитного потока должен удовлетворять нескольким условиям:
- –Магнитный поток Ротора устанавливается и поддерживается постоянным регулятором.
- –Скорость вращения вала двигателя устанавливается и поддерживается постоянной регулятором.
- –Скорость вращения координат постоянна и определяется потоком ротора и крутящим моментом.
- –Проведено математическое описание системы во вращающейся системе координат
x
иy
. - –Ориентация системы координат обеспечивает поддержание проекций потока ротора равными: ψRy = 0, ψR = ψ Rx = const:
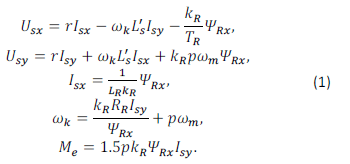
Где:
Usx, Usy, Isx/sub>, Isy, ψRx– проекция на ось напряжения, токов,магнитного потока
ωm– угловая скорость ротора
Me = M load – электромагнитный момент и момент нагрузки
P – количество пар полюсов машины
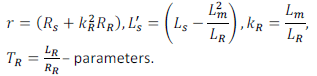
Для выбранного двигателя были рассчитаны соотношения в уравнениях (1) , которые помещены в таблицу 1.
Таблица 1 Расчетные соотношения в уравнениях (1)
| Параметры. | r | Ts | Tr | κR | L’S |
|---|---|---|---|---|---|
| Единицы измерения. | Ω | s | s | – | H |
| Значение | 0,4285 | 0,0046 | 0,2956 | 0,9848 | 0,00196 |
Уравнения (1) позволяют рассчитать токи, напряжения и угловую частоту на выходе инвертора при задании электромагнитного момента и скорости машины. Энергетические характеристики электропривода рассчитываются по уравнениям:
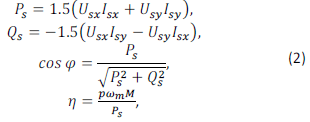
Где:
PS – Активная мощность, QS– Реактивная мощность,cosφ– коэффициент мощности, η – КПД.
Для таких случаев, в соответствии с технологическими требованиями данных производств, необходимо регулирование параметров (обычно скорости) асинхронных электроприводов, поддержание высоких показателей по электрическому КПД и коэффициенту мощности (cos). Даже в режимах работы АД, близких к номинальному, при электрическом КПД 80–92% и cos = 0,8–0,9 общий энергетический КПД составляет 64–83% и имеет тенденцию снижения до 52–70%, если не реализовать специальные энергосберегающие технологии, связанные с регулированием напряжения и реактивной мощности на базе современных статических устройств.
РЕЗУЛЬТАТЫ
На Рис. 1, Рис. На рис.2 приведены расчетные зависимости активной и реактивной мощности в асинхронном электроприводе при изменении крутящего момента и частоты вращения.
Проекции поверхности на базовую плоскость представляют собой зависимость между скоростью и крутящим моментом при постоянной мощности на выходе привода. По этим прогнозам можно судить об ограничениях на диапазон изменения частоты вращения и крутящего момента на выходе асинхронного привода. Активная и реактивная электрическая мощность нелинейно зависят от скорости и крутящего момента на выходе.

Рисунок 1 – Характеристики активной мощности асинхронного электропривода с полевым управлением
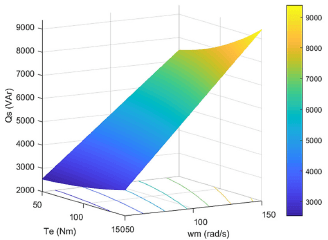
Рисунок 2 – Характеристики реактивной мощности в асинхронном электроприводе с полевым управлением
Математическое описание асинхронного электропривода с прямым регулированием крутящего момента (ДТК)
На системе с ДТК крутящий момент определяется как произведение потока ротора и статора.

Это означает, что знак приращения момента может быть положительным или отрицательным в зависимости от знака приращения ψSy.Система управления электроприводом выполнена во вращающейся системе координат как двухканальная. В канале х
поддерживается постоянный модуль потока статора |ψS| = const.
Управление крутящим моментом осуществляется в канале y
. Управление инвертором осуществляется в соответствии с таблицей оптимальных переключений [13].
Таблица оптимальных переключений записывается в микропроцессорное управление и в зависимости от положения вектора ψS и от знака ΔM определяется, какие транзисторы инвертора должны быть открыты. Все вышесказанное позволяет приступить к разработке математического описания асинхронной системы прямого регулирования крутящего момента.
- Во–первых, следует отметить, что при прямом регулировании крутящего момента осуществляется векторная модуляция в инверторе. Это позволяет заменить выходное напряжение инвертора первой гармоникой.
- Во–вторых, при описании электромагнитных процессов в качестве переменных состояния выбираются ψS и ψRтогдаисходные уравнения принимают вид:
- В–третьих, базовый вектор в DTC–это набор магнитных векторов РотораψR = ψRx = ψR
- В–етвертых, электрическая система управления
строится двухканальной во вращающейся
системе координат. В канале
х
поддерживается постоянный модуль магнитного потока статора. В каналеy
осуществляется управление крутящим моментом. - В–пятых, преобразование управляющих сигналов в сигналы коммутации инвертора осуществляется с помощью таблицы оптимальных коммутаций.
Когда математическое описание системы становится:

Энергетические характеристики асинхронного электропривода с прямым регулированием крутящего момента приведены на рис.3 и рис.4.
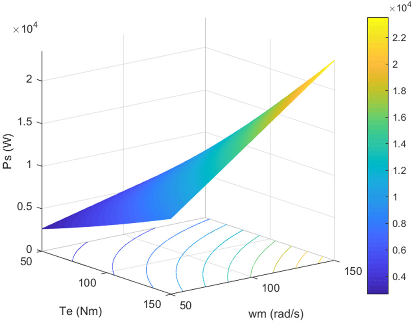
Рисунок 3 – Характеристики активной мощности в асинхронном электроприводе с DTC
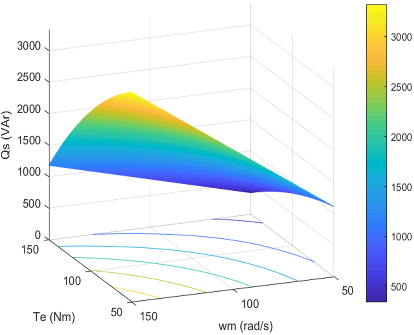
Рисунок 4 – Характеристики реактивной мощности в асинхронном электроприводе с DTC
ОБСУЖДЕНИЕ
В статье проведен расчет силовых характеристик асинхронных электроприводов с векторным управлением. Эти характеристики строятся в пространственных координатах, где скорость и крутящий момент на выходе электропривода задаются переменными состояния. Активная мощность, реактивная мощность рассчитываются как функции скорости и крутящего момента. Авторы рассмотрели большое количество публикаций по асинхронным электроприводам с различными законами управления и не нашли аналогичного подхода при изучении их энергетических характеристик. Поэтому сравнение полученных результаты с известными не возможны. Большинство работ посвящено проектированию асинхронного электропривода и исследованию его динамических свойств.
ЗАКЛЮЧЕНИЕ
Асинхронные электроприводы с векторным управлением имеют не только значительно улучшенные динамические характеристики, но и, как показали вышеприведенные исследования, улучшенные энергетические характеристики. Эти преимущества наиболее заметны при сравнении реактивной мощности, потребляемой электроприводом. При той же механической выходной мощности электропривод с управлением DTC потребляет примерно в 3–3,5 раза больше энергии меньшая реактивная мощность по сравнению с электроприводом с Контроль FOC.
СПИСОК ЛИТЕРАТУРЫ
- F. Blaschke.
Das Prinzip der Feldorientierung–die Grundlage fur die Transvektor–Regulung von Drehfeldmaschienen
. Siemens: Z., 1972, №1, pp. 757– 760. - L. Boychuk. Method of structural synthesis of nonlinear automatic control systems. Energy: Moscow, 1971, p. 321.
- Braslawski, Z. Ishmatov and E. Barac.
Adaptive direct control moment of asynchronous drives
. Electrical engineering, vol. 1, pp. 19–24, 2001, no. 11. - V. Brodovski and E. Ivanov. Elektric drives with frequency– current control. Energy: Moscow, 1974, pp. 168.
- A. A. Bulgakov. A new theory of control rectifiers. Nauka: Moscow, 1970, p. 276.
- M. Depenbrock.
Direct Self–Control (DSC) of Inverter– Fed Induction Machine
. IEEE Transaction On Power Electronics, 1988, Vol. 3, no. 4. - S. G. German Galkin. Virtual laboratory of semiconductor systems in Matlab–Simulink Wednesday. Lane: S. Petersburg, 2013, p. 450.
- K. Kovacs and I. Raz Transitional processes in machines of alternetic current. Gosjenergoizdat: Moscow– Leningrad, 1963, p. 789.
- T. Orlowska–Kowalska. Sensorless induction motor drives. University of Technology Press: Wroclaw, 2003, p. 165.
- O. S. Popow. Elementy teorii systemow – systemy dynamiczne. Politechnika Szczecinska, Wydzial Informatyki: Szczecin, 2005, p. 233.
- A. S. Sandler and R. S. Sarbatov. Automatic frequency control of induction motors. Energiia: Moscow, 1974, p. 163.
- O. Slezhanovskij, L. Dackovskij, I. Kuznetsov, E. Lebedev, L. Tarasenko. The slave systems for control electric drive with semicondactor converters. Energoatomizdat: Moscow, 1983, pp. 342.
- G. G. Sokolovski. AC electric drives with frequency control. Academy: Moscow, 2006, p. 318.
- I. Takahashi, T. Noguchi.
New Quick–Response and High–Efficiency Control Strategy of an Induction Motor
. IEEE Transaction On Industry Application, 1986. Vol. 22, no 5. - D. Tarnapowicz, S. German–Galkin.
Energy optimization of mechatronic systems with PMSG
,3rd International Conference on Energy and Environmental Protection
. 2018, Vol. 46, pp. 1–8. DOI: 10.1051/e3sconf/20184600016.