Аннотация
Исследованы аэродинамические процессы, протекающих в тупиковых выработках небольшой длины, проветриваемых за счёт турбулентной диффузии. Проведено численное моделирование процессов движения воздуха по сквозной выработке, срыва потока на сопряжении с глухой выработкой (для бокового примыкания), образования вихрей в тупике. Исследование выполнено для широкого диапазона поступающих в расчётную область расходов воздуха и для различных геометрических параметров глухой выработки. Определены размеры вихревых структур и скорости течений в тупике. По результатам обработки данных моделирования получены графики зависимостей протяжённости проветриваемой зоны тупика от его высоты и ширины.
Ключевые слова: аэродинамические процессы, численное моделирование, метод контрольных объёмов, турбулентная диффузия, глухая выработка, скорости течения.
Общая постановка проблемы
Согласно федеральным нормам и правилам в области промышленной безопасности «Правила безопасности для угольных шахт» за счёт процессов турбулентной диффузии может организовываться проветривание тупиковых выработок газовых шахт длиной не более 6 м, а негазовых – до 10 м [1]. Экспериментальные исследования процессов прохождения потока воздуха мимо тупиковых выработок проводились ещё в 40 – 50-х годах (В.Н. Воронин [4] и А.М. Карпов [2]). По результатам данных исследований выявлена физическая картина аэродинамических процессов и В.Н. Ворониным введено понятие турбулентной диффузии, как процесса взаимодействия турбулентной свободной струи свежего воздуха и окружающей эту струю смеси воздуха и рудничных газов в пространстве, которое подлежит проветриванию. Карпов А.М. получил различные по величине в зависимости от расположения тупика по отношению к сквозной выработке, устойчивые завихрённые зоны: прямые (3 – 5b), боковые (3 – 4b), обратные (2 – 3b), где b – ширина тупиковой выработки.
Исследования проводились для выработок небольших сечений, закреплённых деревянной крепью, и их результаты для горнотехнических условий современных шахт могут существенно отличаться.
Для изучения аэродинамических процессов в глухих выработках выполнено численное моделирование. Для этой цели выбран свободно распространяемый пакет OpenFOAM (The OpenFOAM Foundation Ltd) [5]. Для подготовки исходных данных, таких, как задание геометрии расчётной области, построение сетки и постановка граничных условий, выбран мультиблочный сеточный генератор blockMesh. Данная утилита делит расчётную область на гексаэдры. Парадигма создания сеточных структур в OpenFOAM позволяет использовать вырожденные формы шестигранников. Для численного решения выбран стандартный решатель simpleFoam (решатель для стационарных задач несжимаемого, турбулентного потока; используется алгоритм SIMPLE). Визуализация и обработка результатов вычислений выполнена с использованием постпроцессора ParaView (поставляется вместе с OpenFOAM и также является свободно распространяемым). ParaView обеспечивает визуализацию скалярных и векторных полей, линии тока, изоповерхности, получение информации о нужном поле в точке или вдоль некоторой линии и т.п.
Создан вычислительный кластер типа Beowulf
на базе:
- –3 моноблоков iRU с процессорами Intel Core i5–3330, с общим количеством вычислительных ядер 12;
- – коммутатора D-Link DGS–1005/D со скоростью пакетной передачи данных до 1 Гбит/с (сеть Ethernet).
Вычислительный кластер позволил уменьшить время расчётов по сравнению с одиночным компьютером, декомпозируя расчётную область на параллельно выполняемые ветви, которые обмениваются данными по связывающей сети. Для оценки увеличения производительности с использованием вычислительного кластера типа Beowulf
проведён расчёт движения воздуха по прямолинейному участку горной выработки (25 тыс. гексаэдров, общее число итераций 1000). Результаты расчёта сведены в табл. 1.
| Число ядер, шт. | 1 | 2 | 4 |
|---|---|---|---|
| Продолжительность решения, с. | 105,6 | 56,75 | 46,02 |
| Повышение производительности, в разы | – | 1,86 | 2,29 |
Таким образом, использование параллельных алгоритмов при расчётах с помощью пакета OpenFOAM на вычислительном кластере позволяет существенно сократить время расчётов. Особенно при создании расчётных областей больших размеров и использовании мелкой сетки.
Для исследования аэродинамических особенностей тупиков (боковое примыкание) создана базовая модель, приведённая на рис. 1. Модель состоит из четырёх блочных суперэлементов, каждый из которых сеточный генератор blockMesh декомпозирует на гексаэдры. Числами на рис. 1 обозначены вершины суперэлементов. Длина и ширина сквозной выработки (без учёта размеров сопряжения) составляют 80 и 6 м соответственно для всех серий экспериментов. Длина тупиковой выработки 20 м.
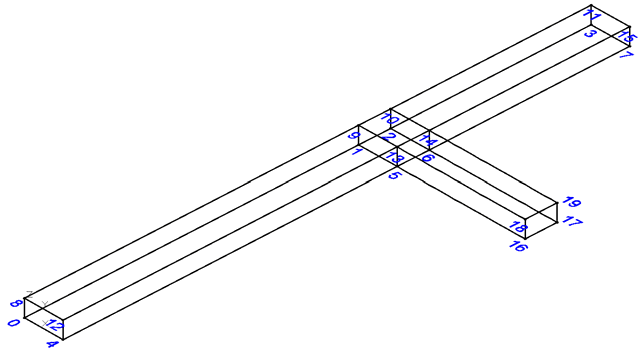
Рисунок 1 – Базовая модель, созданная для исследования аэродинамических особенностей тупиков
Численное моделирование выполнено для условий, приведённых в табл. 2. Всего проведены 90 серий экспериментов.
Таблица 2 Матрица начальных условий, для которых выполнено моделирование

На рис. 2 приведено распределение скоростей течений в глухой выработке для различных скоростей движения воздуха в сквозной выработке (данные для S = 12 м2, высота 2,5 м, ширина 4,8 м). Использованы обозначения: чёрные вертикальные линии – границы вихря (рис. 3), красная горизонтальная пунктирная линия – минимальная скорость потока (0,15 м/с).

Рисунок 2 – Распределения скоростей движения воздуха в глухой выработке при различных скоростях движения потока в сквозной выработке (по оси выработки)
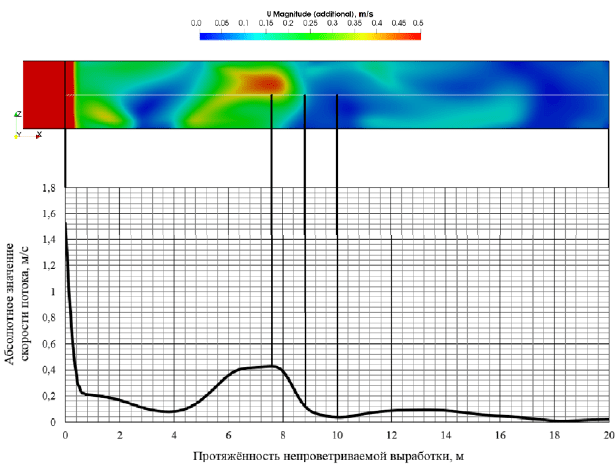
Рисунок 3 – Схема, поясняющая принцип определения размеров первого вихря в тупиковой выработке (по оси выработки)
На рис. 4 – 6 приведены линии тока в тупиковой выработке (размеры вихрей) для высоты выработки 2,5 м и ширины 3,0, 4,8, 6,0 м, средняя скорость потока по сквозной выработке 3 м/с. Для обозначения скоростей движения потока использованы две шкалы цветности: U Magnitude (main), m/
для сквозной выработки, U Magnitude (additional), m/s
для тупиковой выработки.
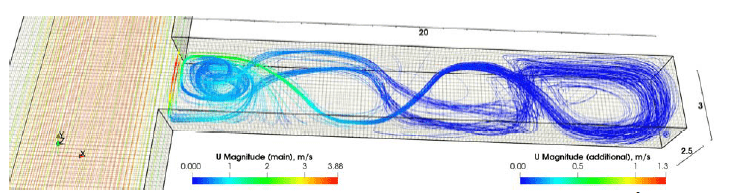
Рисунок 4 – Линии тока для ширины выработки 3 м (S = 7,5 м2)

Рисунок 5 – Схема, поясняющая принцип определения размеров первого вихря в тупиковой выработке (по оси выработки)
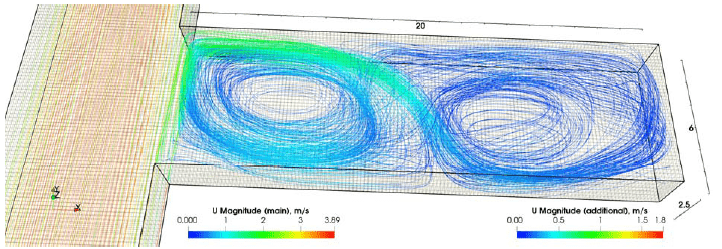
Рисунок 6 – Схема, поясняющая принцип определения размеров первого вихря в тупиковой выработке (по оси выработки)
На рис. 7, 8 приведены полученные зависимости протяжённости проветриваемой зоны выработки от её ширины и высоты соответственно.
Обеспечивающая часть – совокупность программных и технических средств обеспечения системы автоматического управления проветриванием.

Рисунок 7 – Зависимость средней протяжённости зоны вихря от ширины тупиковой выработки с боковым примыканием: чёрный цвет линий – высота 2,0 м; фиолетовый цвет линий – высота 2,5 м; синий цвет линий – высота 3,0 м
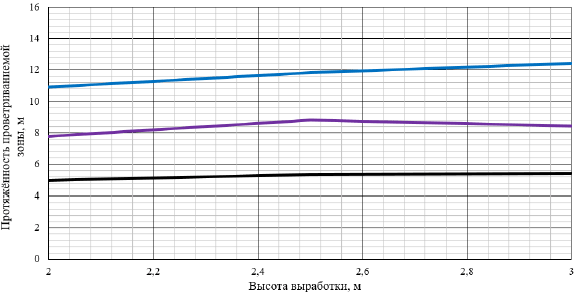
Рисунок 8 – Зависимость средней протяжённости зоны вихря от высоты тупиковой выработки с боковым примыканием: чёрный цвет линий – ширина 3,0 м; фиолетовый цвет линий – ширина 4,8 м; синий цвет линий – ширина 6,0 м
По результатам численных исследований установлено, что для глухой выработки с боковым примыканием:
- требования федеральных норм и правил в области промышленной безопасности [1] в целом являются обоснованными, но только для тех случаев, когда скорости потока в сквозной выработке более 1 м/с. В этом случае обеспечивается минимальная скорость течения в тупике 0,15 м/с на расстояниях от устья до 6 м (для газовых шахт);
- размер зон, проветриваемых за счёт турбулентной диффузии, в основном зависит от ширины выработки, высота выработки не имеет определяющего значения;
- вихревые течения носят сложный характер, образуется плоская свободная струя (по В.Н. Воронину), проветривающая тупик по восьмиобразной схеме.
Список литературы
- Приказ Федеральной службы по экологическому, технологическому и атомному надзору от 19.11.2013 № 550
Об утверждении Федеральных норм и правил в области промышленной безопасности
(зарегистрировано в Минюсте России 31.12.2013, рег. № 30961, ред. от 25.09.2018).Правила безопасности в угольных шахтах
- Скочинский А. А., Комаров В. Б. Рудничная вентиляция. М.: Углетехиздат, 1959. 632 с.
- Воронин В. Н. Основы рудничной аэрогазодинамики / под общ. ред. А. А. Скочинского. М.: Углетехиздат, 1951. 491 с.
- Аэрология горных предприятий: учебник для вузов / К. З. Ушаков, А. С. Бурчаков, Л. А. Пучков, И. И. Медведев. М.: Недра, 1987. 421 с.
- Попов А. Ю. Об использовании свободно распространяемого программного обеспечения для решения задач вычислительной гидроаэродинамики // Вестник МГТУ им. Н.Э. Баумана. Сер.
Естественные науки
. 2011. S1. C. 96 – 108. - Говорухин Ю. М., Криволапов В. Г., Палеев Д. Ю. Использование CFD-пакетов при решении задач вентиляции шахт и подготовке горных инженеров // Наукоёмкие технологии разработки и использования минеральных ресурсов. Новокузнецк: Изд-во СибГИУ, 2019. № 5. С. 453 – 458.
- Говорухин Ю. М., Фрянов В. Н., Палеев Д. Ю. Численное моделирование взаимодействующих геомеханических и аэродинамических процессов на выемочном участке // Известия Тульского государственного университета. Науки о Земле. 2019. Вып. 2. С. 288 – 299.
- Moukalled F., Mangani L., Darwish M. The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM and Matlab. Springer, 2016. 817 p.
- OpenFOAM. The OpenFOAM Foundation: User Guide. Version 7. 2019. 237 p.
- Ayachit U. The ParaView Guide. Community Edition. Updated for ParaView version 5.4. 2017. 254 p.
- Jasac H. Error Analysis and Estimation for the Finite Volume Method with Application to Fluid Flows: Thesis for the Degree of Doctor of Philosophy of the University of London and Diploma of Imperial College. June 1996. 396 p.
- Ying W., Feng S. The performance of OpenFOAM in Beowulf clusters // Proceeding of the 2nd International Conference on Computer Science and Electronics Engineering (ICCSEE). 2013. Р. 1683 – 1686.