Моделирование работы магистрального конвейерного транспорта шахты
Авторы: Д. Л. Клименко, Б. В. Гавриленко
Источник: Автоматизация технологических объектов и процессов. Поиск молодых: сборник научных трудов ХХ международной научно-технической конференции аспирантов и студентов в г. Донецке 26–28 мая 2020 г. – Донецк: ДОННТУ, 2020. – 452 с.
Аннотация
В статье рассмотрены особенности работы конвейерного транспорта горнодобывающих предприятий. Разработана имитационная модель транспортной сети шахты с использованием сетей Петри. Синтезирована модель транспортной системы шахты, учитывающая неравномерности грузопотока сыпучего материала. Проанализированы результаты имитационного моделирования.
Конвейерный транспорт является основным энергоемким звеном процесса доставки полезного ископаемого от очистных забоев на поверхность шахты. В свою очередь, с поверхности шахты по горным выработкам осуществляется доставка вспомогательных материалов, грузов, оборудования и людей к месту работы, в том числе при помощи электровозного транспорта.
Эффективность работы подземного конвейерного транспорта горнодобывающего предприятия зависит от:
- структуры и топологии существующей транспортной сети, содержащей непрерывные и дискретные по режимам работы элементы с ограниченной пропускной способностью;
- неравномерности грузопотоков, распределенных в пространстве и времени;
- коэффициента готовности и надежности отдельных элементов транспортной сети.
Эффективность работы подземной транспортной сети горного предприятия может быть повышена путем устранения неравномерности грузопотоков, снижения удельных энергетических затрат и оптимизации режимов работы отдельных элементов подземной транспортной сети.
Для анализа структурной схемы подземной транспортной сети шахты (рис. 1) разработана имитационная
модель, учитывающая случайный характер изменения грузопотоков, технологические параметры и режимы работы
элементов очистной забой
, конвейерная линия
, аккумулирующий бункер
и
подъемная установка
. Имитационное моделирование транспортной сети производилось с использованием
сетей Петри [1].

Рисунок 1 – Структурная схема транспортной сети горного предприятия
Непрерывный грузопоток горной массы представляет собой перемещение в системе конвейерного транспорта шахты дискретных объемов:
где Δt – шаг дискретизации грузопотока по времени;
k = T⁄Δt – количество дискретных объемов за время дискретизации T;
f(ti) – объем горной массы за время ti.
Согласно [2], при дискретизации непрерывного грузопотока масса дискретного объема груза не должна превышать 1 тонну. Рассмотрим технологические особенности и режимы работы отдельных элементов структурной схемы транспорта шахты (рис.1) с использованием сетей Петри.
Модель очистного забоя (рис. 2) представлена двумя входами: временем работы Zw (время одного прохода очистным комбайном линии забоя) и временем остановки Zs, (время на совершение концевых операций), а также одним выходом – величина грузопотока Qi.
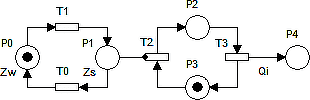
Рисунок 2 – Модель работы очистного забоя
Токены перемещаются между позициями P0 и P1, а также P2 и P3. Время задержки Zw токена в позиции P0 имитирует время работы очистного забоя, в течение которого непосредственно производится добыча полезного ископаемого. В свою очередь, время задержки Zs токена в позиции P1 имитирует время выполнения в очистном забое концевых операций (выемка и крепление ниш, подготовка комбайна к выемке угля, перестановка крепи сопряжения и т. д.). Во время остановки очистного забоя ингибиторная дуга перекрывает переход T2, что в свою очередь останавливает перемещение токенов между позициями P0 и P1, P2 и P3. На выходе модели формируется грузопоток – количество токенов Qi, которое соответствует объему добычи из очистного забоя.
Процесс перемещения горной массы одним конвейером характеризуется инициированной задержкой времени:
где Li – длина i-го конвейера;
Vi – скорость i-го конвейера.
Таким образом, инициированная задержка токена в переходе Ti, моделирующем работу конвейерной линии (рис. 3) из нескольких конвейеров, составляет:
где Δti – время задержки i-го конвейера;
n – количество конвейеров в линии.
Рисунок 3 – Модель работы конвейерной линии
Для исключения просыпания полезного ископаемого максимум входного грузопотока Qвх не должен превышать пропускную способность Qт конвейера.
Аккумулирующий бункер представлен движением токенов по сети Петри с тремя позициями P0, P1 и P2 и тремя переходами T0, T1 и T2 (рис. 4).
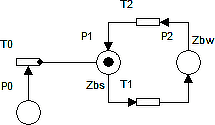
Рисунок 4 – Модель работы аккумулирующего бункера
Позиция P0 представлена аккумулирующим бункером, а переход T0 – питателем бункера. Время задержки Zbs токена в позиции P1 имитирует процесс заполнения горной массой аккумулирующего бункера при остановленном питателе бункера (ингибиторная дуга перекрывает переход T0). Время задержки Zbw токена в позиции P2 имитирует процесс разгрузки аккумулирующего бункера, переход T0 открыт.
Для уменьшения вероятности перегрева приводов питателя аккумулирующего бункера время задержки Zbw принимается не менее 10 минут.
Модель подъемной установки состоит из двух позиций P0, P1 и переходаT0 (рис. 5).

Рисунок 5 – Модель работы подъемной установки
Позиция P0 имитирует работу бункера для загрузки скипов, а позиция P1 – поверхность. Инициированная задержка Zlift перехода T0 имитирует время цикла работы подъемной установки [3]:
где Q – грузоподъемность подъемного сосуда;
Aчас – часовая производительность подъемной установки.
Грузоподъемность скипа двухсосудного подъема [4]:
где Hш – высота подъема, принимается Hш = 273 м;
Θ – время на процесс загрузки (разгрузки) скипа, принимается Θ = 20 с;
Aчас – часовая производительность подъемной установки.
Согласно выражению (5) грузоподъемность скипа 1СН20-1 составляет Q = 15 т.
Часовая производительность подъемной установки [3] определяется из выражения:
где c – коэффициент резерва подъемной установки, c = 1,2;
b – количество рабочих дней в году, принимается b = 300 сут;
t – количество часов работы подъемной установки в сутки, принимается t = 16 ч;
Aгод – годовая производительность шахты, составляет 2500000 т.
В соответствии с выражением (6) часовая производительность подъемной установки составляет Aчас = 625 т/ч.
Дуги, соединяющие множество позиций с множеством переходов, имеют два направления – от позиции к переходу и наоборот. Вес дуги определяет количество токенов, которое переносит дуга в единицу времени от одного элемента схемы к другому.
Вес дуг модели конвейерной линии определяется конвейером с наименьшей пропускной способностью.
Вес дуг модели работы подъемной установки определяется грузоподъемностью применяемого сосуда.
На рисунке 6 приведена разработанная имитационная модель системы подземного транспорта горного предприятия в виде сети Петри.
Исследование разработанной имитационной модели работы транспортной сети горного предприятия осуществлялось с применением программного пакета HPSim 1.1.
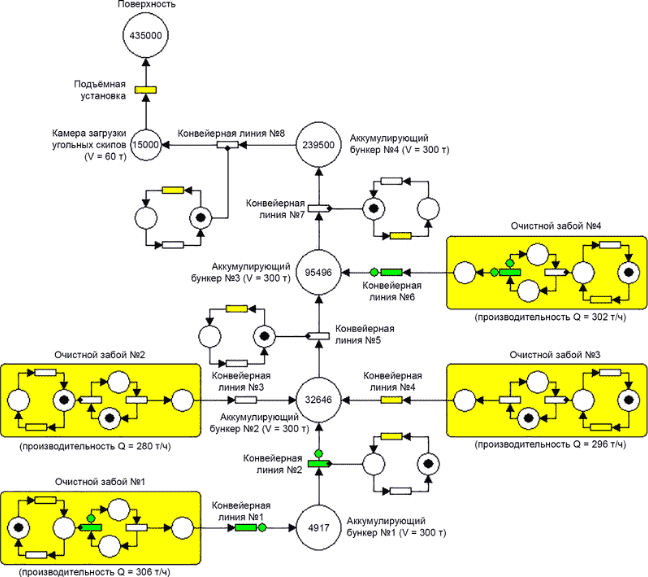
Рисунок 6 – Модель системы подземного транспорта угля на горном предприятии
Непрерывный поток определяется движением по транспортной сети дискретных объемов груза условной массой один килограмм. Время моделирования составило 21600 единиц модельного времени, что соответствует шестичасовой рабочей смене на шахте. Результаты имитационного моделирования работы очистных забоев, аккумулирующих бункеров и процесса транспортирования полезного ископаемого на поверхность шахты соответственно приведены на рисунках 7, 8 и 9.
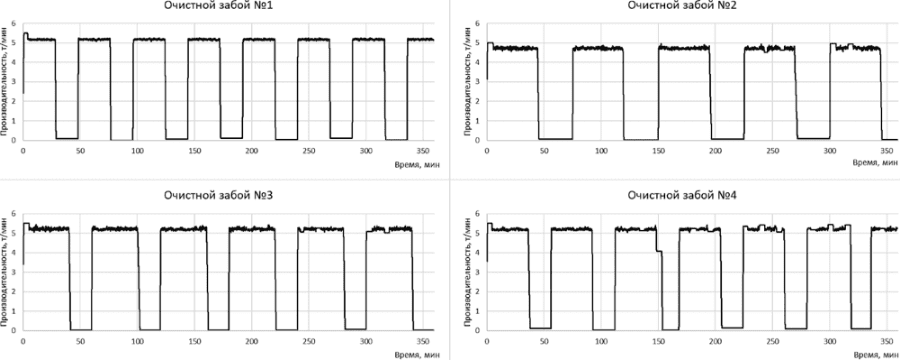
Рисунок 7 – Результаты моделирования работы очистных забоев

Рисунок 8 – Результаты моделирования работы аккумулирующих бункеров
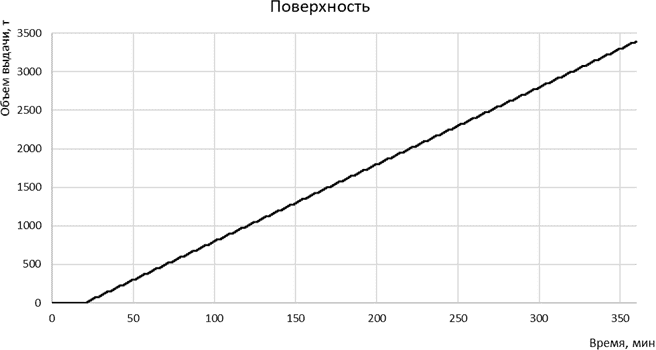
Рисунок 9 – Результаты моделирования грузопотока угля на поверхность шахты
Анализ результатов моделирования показывает, что эффективность работы конвейерного транспорта шахты зависит от пропускной способности и режимов работы отдельных элементов транспортной цепочки, а также параметров аккумулирующих бункеров.
Разработанная модель системы подземного транспорта шахты позволяет: оценивать аккумулирующую способность магистральной конвейерной линии при возникновении аварийных ситуаций, производить прогноз грузопотоков в транспортных системах с различной топологией, определять оптимальные параметры аккумулирующих бункеров для сглаживания неравномерности грузопотоков.
Разработанная имитационная модель может быть реализована при создании систем автоматического управления подземным конвейерным транспортом шахты.
Перечень ссылок
- Васильев В. В., Кузьмук В. В. Сети Петри, параллельные алгоритмы и модели мультипроцессорных систем. – Киев.: Наук. Думка, 1990. – 212 с.
- Lebedev A., Staples P. Simulation of materials handling systems in the mines: Two case studies // Simulation. 1998.
- Хрусталев И. К. О режиме работы неуравновешенной подъемной установки. – Томский политехнический институт, 1956. – 13 с.
- Дроздова Л. Г. Стационарные машины: учеб. пособие. – Владивосток: Изд-во ДВГТУ, 2007. – 157 с.