Аннотация
Предложена методика оценки отношения оптического сигнала к шуму (OSNR) с использованием низкополосных когерентных приемников и обучающих последовательностей Голея (TSs) для когерентных оптических систем с автоматизированной оценкой каналов. Те же Тсс, которые используются для оценки каналов в когерентной оптической системе, используются и для оценки ОСНО с использованием низкоскоростных приемников. Метод основан на анализе спектральных свойств ТСС в пределах полосы пропускания приемников и, таким образом, может быть принят для приемников с низкой полосой пропускания и для целей распределенного оптического мониторинга. Показано, что метод имеет точность 1 дБ для 40-Гбит/с поляризационно-мультиплексированной квадратурной фазовой манипуляции и 16-квадратурной амплитудной модуляции когерентных однонесущих оптических систем при передаче до 1000 км. Индексные термины-обучающие последовательности, отношение оптического сигнала к шуму, низкочастотный, когерентный приемник.
Введение
Спрос на приложения с высокой пропускной способностью привел к переходу от использования прямого обнаружения к когерентному обнаружению для будущих оптических сетей. Используя когерентное обнаружение, можно использовать высокоуровневые форматы модуляции, такие как поляризационно - мультиплексированная (PM) квадратурная фазовая манипуляция (QPSK) и 16-квадратурная амплитудная модуляция (16QAM), которые значительно повышают эффективность передачи. Когерентные приемники также позволяют контролировать и компенсировать линейные нарушения, такие как хроматическая дисперсия (CD) и дисперсия поляризационных мод (PMD), непосредственно из принимаемого сигнала. Обычно существует два подхода к оценке линейных нарушений с использованием когерентных приемников: слепой подход, использующий градиентные алгоритмы; и автоматизированный подход (DA), использующий часть полосы пропускания системы для обучающих последовательностей (TSs). Системы автоматизированной цифровой обработки сигналов (ЦОС) обладают высокой точностью и надежностью оценки каналов, а также совместимостью с оптическим мониторингом производительности (ОПМ), также может быть оценена из Тсс автоматизированных систем на конечных приемниках независимо от фактического потока данных, что обеспечивает большую гибкость при проектировании ЦОС приемника по сравнению с неавтоматизированным методом оценки OSNR. Хотя эти методы оценки OSNR практически не требуют дополнительных аппаратных затрат, они полагаются на полноскоростные когерентные приемники и поэтому не являются оптимальными для распределенного мониторинга всей сети. Кроме того, оптические сети эволюционировали от одноточечной к многолучевой маршрутизации, и недорогое решение для мониторинга, использующее низкоскоростное аппаратное обеспечение для распределенного мониторинга оптической сети, будет востребовано. В этом письме мы предлагаем и демонстрируем метод оценки внутриполосного оптического отношения сигнал / шум (OSNR) для когерентной оптической системы С одной несущей и автоматизированным DSP, использующим низкочастотные когерентные приемники и суб-Найквист-скорость дискретизации. Этот метод использует доступные TSs когерентной оптической системы с поддержкой данных и, таким образом, может обеспечить недорогое распределенное решение мониторинга для когерентных оптических систем с поддержкой данных DSP. Экспериментально показано, что данная методика позволяет оценить широкий диапазон ОСНО с точностью до 1 дБ при передаче до 1000 км.
2. Оценка OSNR с использованием данныйх с низкой пропускной способностью
Когерентная оптическая система с поддержкой данных использует обучающие последовательности для обработки сигналов. Были предложены оптимальные последовательности, такие как последовательности постоянной амплитуды нулевой автокорреляции (CAZAC) и последовательности Голея. Последовательности голея представляют собой пару комплиментарных последовательностей S1 и S2, удовлетворяющих свойству спектра мощности: G[k]= |S1[k] / 2 + / S2[k] / 2 = L (1) где S1[k] и S2[k] - дискретное преобразование Фурье исходной последовательности S1 и S2 соответственно, а L-константа, связанная с длиной каждой последовательности. Известно, что пара последовательностей казака, каждая из которых имеет постоянный спектр мощности, также удовлетворяет свойству Голея. Однако по сравнению с последовательностями CAZAC последовательности Голея обладают аналогичной производительностью, но с дополнительным преимуществом наличия простой и независимой от длины группировки и, таким образом, более подходят для коммерческой реализации когерентных оптических систем с поддержкой данных [6]. Для когерентных оптических систем с поляризационным мультиплексированием 2х2 четыре последовательности Голея расположены в кодовой структуре Аламоути, за которой следует фактический кадр данных, как показано на рис. 1 при этом S1 и S2 являются двумя ортогональными. Последовательности голея; S1∗, S2∗ являются комплексным сопряжением исходных последовательностей S1 и S2 соответственно, а CP указывает малый циклический префиксный блок для каждой последовательности.

|
Рисунок 1 - обучающие последовательности Голея в когерентной оптической системе ПМ.
Сначала мы рассмотрим обучающие последовательности Голея, захваченные с полной скоростью дискретизации, вдвое превышающей скорость передачи данных системы, и с использованием приемника с полной полосой пропускания. В приемнике после дискретизации сигнала со скоростью Найквиста и последующей синхронизации времени могут быть восстановлены четыре последовательности, содержащие переданные последовательности с линейным ухудшением плюс системный шум. В частотной области четыре принятых TSs могут быть выражены следующим образом: R1[k] R2[k] Σ = H [k] . S1[k] ∗ S2[k]∗ Σ + W [k] (2) где H[k] - матрица переноса линейных нарушений, состоящая в основном из хроматической дисперсии (CD) и поляризационной модовой дисперсии (PMD). S1[k] и S2[k] - дискретное преобразование Фурье (DFT) исходных последовательностей S1 и S2 (дискретизированных со скоростью Найквиста); R1[k] и R2[k] - DFT принятых последовательностей Голея S1 и S2 в приемнике; а W[k] - спектральная плотность шума. Далее мы предполагаем, что шум распределен по Гауссу с нулевым средним. Для применения с использованием низкополосных приемников эффект PMD мал и незначителен, в то время как CD является всепроходным фильтром с квадратичной фазовой характеристикой в частотной области и, таким образом, не влияет на комплиментарное свойство кодов Голея, использующих спектр мощности. Пренебрегая влиянием линейных нарушений, свойство Голея полученной Тсс на рентгеновскую поляризацию может быть выражается как: G[k] = | R1[k]|2 + |R2[k]|2 = |S1[k]|2 + |S2[k]|2 + 2 |W [k]|2 +2Re S1[k]∗W [k] + 2Re S2[k]∗W [k] (3) w W[k] - спектральная плотность шума, а Re (.)-вещественная часть (.). аналогичное выражение уравнения (3) можно получить для сигнала при Y-поляризации и опустить для ясности. Дисперсия уравнения (3) после математических манипуляций и упрощения может быть выражена как: V G k G k 2 = 4 .[W [k]]4 + [Re (S1[k]W [k])]2 + [Re (S2[k]W [k])]2Σ где (.) обозначает ожидаемое значение (.). Это видно из эквалайзера. (4) Что V пропорционально ожидаемому значению W[k]2 и, таким образом, связано с системой SNR. Инжир. 2 показан пример моделирования для эквалайзеров. (3) и (4) с двумя различными значениями OSNR с 256-символьными последовательностями Голея и видно, что изменение значения OSNR (а следовательно, и изменение значения SNR) вызывает изменения в вариации спектра сигнала TSs G[k] и, в свою очередь, вызывает изменение расчетного значения V. Таким образом, уравнение (3) сначала решается для широкого диапазона значения SNR и результаты хранятся в виде заранее определенной таблицы поиска. Затем значение SNR системы оценивается путем вычисления Центрального второго момента спектра принятого сигнала и последующего использования заранее определенных результатов для SNR оценка. Наконец, OSNR вычисляется из SNR путем первого измерения спина к спине значения SNR без какого–либо дополнительного шума ASE и учета опорной полосы пропускания шума.
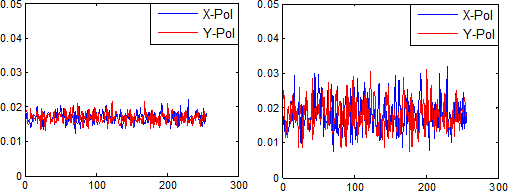
|
Рисунок 2 - Частотного спектра Г[К] из Голей пара на обеих поляризациях с(а) SNR = 22 дБ и (Б) SNR = 12 дБ.
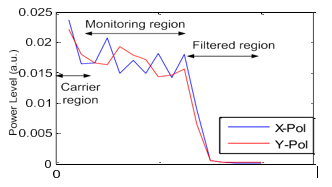
|
Рисунок 3 - Cмоделированный частотный спектр Тсс захваченного сигнала и область мониторинга OSNR с фильтром 800 МГц и частотой дискретизации 2,5 ГГц..
Поскольку предлагаемый метод использует спектральные свойства в частотной области, для оценки SNR с использованием низкой скорости дискретизации и низкочастотного приемника SNR оценивается с использованием оцененных спектральных составляющих в пределах ширины полосы приемника. Скорость дискретизации должна быть примерно в два раза больше полосы пропускания низкоскоростного приемника, используемого для оценки SNR. Инжир. 3 показан пример спектра TSs сигнала 10 Гбод, отфильтрованного фильтром 800 МГц и дискретизированного на 2,5 ГГц с OSNR 22 дБ в моделировании. На спектральные компоненты в самой правой области (за пределами 800 МГц) влияют фильтры, в то время как на спектральные компоненты в самой левой области влияют пик несущего лазера и ширина лазерной линии. После удаления спектральных компонентов в этих двух областях SNR можно оценить, используя оставшиеся спектральные компоненты в пределах области мониторинга. На рис.4 показано нормированное значение V для значения OSNR 22 дБ по отношению к различным углам поворота поляризации. Видно, что спектральное свойство Голея последовательности могут поддерживаться при различных углах поворота поляризации с очень небольшим количеством искажений. Таким образом, SNR можно оценить без предварительной компенсации вращения поляризации.

|
Рисунок 4 - Нормированная дисперсия с разной поляризацией вращения для SNR=22дб в моделировании.

|
Рисунок 5 - Экспериментальная установка.
3. Экспериментальная установка
На рис. 5 показана экспериментальная установка для оценки OSNR с использованием низкочастотного когерентного приемника для автоматизированной обработки данных. Единая несущая система. Обучающие последовательности представляют собой 128-символьные последовательности Голея с 4-символьными циклическими префиксами, а созвездия последовательностей разработаны в соответствии с форматом модуляции системы. Полноскоростной передатчик состоит из одного генератора произвольной формы сигнала (AWG), фильтров нижних частот (LPF) и усилителей (AMP) для генерации потока данных со скоростью 10 Гбод, в результате чего системные скорости передачи данных PM-QPSK и PM-16QAM составляют 40 Гбит/с и 80 Гбит/с соответственно. Случайно сгенерированный блок данных добавляется к блоку TSs с отношением TS к данным 1: 99 (отношение накладных расходов 1%). Сигнал разделяется поляризационным светоделителем (PBS), и линия задержки 27,2 НС используется на одной поляризации для эмуляции Y-поляризации. TSs разработаны таким образом, чтобы соответствовать этой линии задержки, аналогичной конструкции в, чтобы эмулировать обе поляризации системы С одной несущей, управляемой данными. Сигналы на обеих поляризациях затем объединяются вместе с помощью поляризационного объединителя Пучков (PBC), а затем соединяются в рециркуляционный контур с циклом синхронизации, определяющим общую длину передачи, чтобы эмулировать 1000-километровую стандартную передачу одномодового волокна (SSMF) для системы PM-QPSK и 400-километровую передачу SSMF для системы PM-16QAM. Петля состоит из двух пролетов 50-километрового волокна с согласованными волоконными усилителями, легированными эрбием (EDFA), и оптическими полосовыми фильтрами (OBPF). На стороне приемника для управления уровнем ОСНР используется усиленный источник спонтанного излучения (АСЭ), состоящий из двух каскадных волоконных усилителей, легированных эрбием (ЭДФА), и одного оптического полосового фильтра. Затем сигнал разделяется на два тракта с помощью ответвителя с соотношением 9: 1. 10% - ный путь подается в оптический анализатор спектра (OSA), чтобы независимо измерьте OSNR, в то время как другой путь подается в сбалансированный когерентный приемник для обнаружения I и Q компонентов сигнала. Низкочастотный приемник эмулируется четырьмя электрическими фильтрами нижних частот (ФНЧ) частотой 0,8 ГГц, подключенными к выходам стандартного сбалансированного приемника. Затем сигналы захватываются 4-канальным осциллографом реального времени, работающим со скоростью 2,5 GSamples/s для автономной обработки.Поскольку CD и компенсация смещения частоты (FO) необходимы для синхронизации времени, системный CD сначала оценивается с использованием низкочастотной реализации метода автоматизированной оценки данных, предложенного в. Это значение затем используется для компенсации CD с использованием низкочастотной реализации метода перекрытия частотной области с передаточной функцией CD, определяемой как: HCD( f ) = exp.− jπ Dλc f Где HCD (f) - передаточная функция CD, D-расчетное значение дисперсии, c-скорость света, λ-длина лазерной волны и 1,25 ГГц f 1,25 ГГц для скорости дискретизации 2,5 ГГц. FO компенсируется оценкой несущего пика и перемещением этого пика обратно в центр спектра. После КР и ФО компенсацию, цикловая синхронизация осуществляется для извлечения тренировочных последовательностей, создав фильтруют и уменьшается С1 последовательность прохождения полной скорости Голай С1 последовательности через ряд цифровых фильтров в среде MATLAB и вниз-для отбора проб отфильтрованной последовательности, чтобы соответствовать сигнал частота обновления. В результате получается аппроксимированная версия последовательности S1, отфильтрованная фильтром нижних частот 800 МГц и дискретизированная со скоростью 2,5 ГС/с, которая может быть использована для синхронизации времени с использованием кросс-корреляции, как показано на рис. 6(а). На рис.6(б) показан индекс корреляции для синхронизации кадров с использованием описанного выше метода, и видно, что при использовании отфильтрованной последовательности местоположение последовательности в принимаемом сигнале может быть расположено по пику в индексе корреляции.

|
Рисунок 6 - Экспериментальная установка.
4. Измерения и обсуждения
На рис.7 показаны расчетные значения OSNR по отношению к реальному OSNR, измеренному с помощью OSA как для передачи back-to-back (B2B) в когерентных системах с одной несущей с использованием модуляции PM-QPSK и PM-16QAM для матов. Полоса пропускания приемника установлена на уровне 800 МГц,а сигнал улавливается со скоростью 2,5 ГС/С. Каждая точка данных представляет собой в среднем 30 захватов с максимальным отклонением в каждом измерении, построенном в виде баров ошибок. Видно, что для широкий диапазон SNR, оценка точна при всех измерениях в пределах 1 дБ как для форматов модуляции PM-QPSK, так и для форматов модуляции PM-16QAM. Для случая обратной передачи высокая ошибка оценки возникает при очень высоком OSNR из-за остаточного системного шума, как и в большинстве когерентных приемных методов широкий диапазон SNR, оценка точна при всех измерениях в пределах 1 дБ как для форматов модуляции PM-QPSK, так и для форматов модуляции PM-16QAM. Для случая передачи спина к спине высокая ошибка оценки возникает при очень высоком OSNR из-за остаточного системного шума, как и в большинстве когерентных приемников на основе техники.
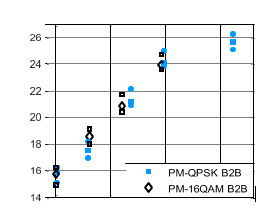
|
Рисунок 7 - среднеквадратичная погрешность оценки для различных полос пропускания приемника для 1000-километровой передачи PM-QPSK с различными значениями OSNR.
На рис. 8 показаны расчетные значения OSNR по сравнению с реальными значениями OSNR, измеренными OSA после передачи 1000 км PM-QPSK и 400 км PM-16QAM с использованием рециркуляционного контура с максимальными отклонениями, построенными в виде баров ошибок, и видно, что оценка также точна как для PM-QPSK, так и для PM-16QAM в широком диапазоне значений OSNR.
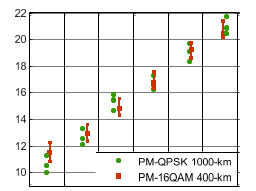
|
Рисунок 8 - расчетный OSNR по сравнению с реальным OSNR в экспериментах после 1000-километровой передачи с фильтрами 800 МГц.
На рис. 9 показана среднеквадратичная (среднеквадратичная) ошибка оценки расчетных значений OSNR по отношению к реальным значениям OSNR в зависимости от требуемой полосы пропускания приемника для передачи 1000 км PM-QPSK. Каждая точка данных также основана на 30 захватах блоков TSs, и эффект различных полос пропускания приемника эмулируется путем увеличения области мониторинга в пределах требуемой полосы пропускания сигнала полной полосы пропускания. Можно видеть, что при увеличении полосы пропускания приемника по мере того, как оценщик имеет больше выборок для работы, наблюдается лишь незначительное увеличение срока действия около 0,1 дБ. В целом можно сделать вывод, что оценка с использованием низкоскоростных приемников является точной с погрешностями в пределах 1 дБ и является подходящим методом для автоматизированных когерентных оптических систем.

|
Рисунок 9 - среднеквадратичная погрешность оценки для различных полос пропускания приемника для 1000-километровой передачи PM-QPSK с различными значениями OSNR.
5. Выводы
Автоматизированные оптические системы С одной несущей являются очень перспективной технологией для будущих оптических сетей. Используя обучающие последовательности, можно выполнять быструю и надежную оценку и выравнивание каналов. Мы показали, что, используя тот же блок TSs, который используется для оценки каналов приемников в когерентных оптических системах с поддержкой данных, OSNR можно оценить с помощью когерентного приемника с низкой полосой пропускания и суб-Найквист-скоростью дискретизации. Методика продемонстрирована в экспериментах, как для систем 40 Гбит/с PM-QPSK, так и для систем 80 Гбит/с PM-16QAM, для оценки широкого диапазона Оснрр с точностью до 1 дБ после передачи до 1000 км. Данная методика совместима со стандартной автоматизированной технологией передачи данных и является перспективным компонентом при проектировании в будущем.