Блочно-ориентированная модель системы автоматического управления регуляторами расхода воздуха в шахтной вентиляционной сети

Аннотация

Завадская Т. В. Блочно-ориентированная модель системы автоматического управления регуляторами расхода воздуха в шахтной вентиляционной сети В статье представлено математическое описание, разработаны блочно-ориентированные модели шахтной вентиляционной сети (ШВС) и системы автоматического управления (САУ) при помощи среды для моделирования, имитации и анализа динамических систем Simulink. Составлена блочно-ориентированная (БО) модель взаимодействия ШВС и САУ с добавлением блока задания начальных условий. Получены результаты изменения расходов воздуха при проведении ряда экспериментов по подключению САУ в ветви ШВС (соответствующие выемочным участкам). По результатам экспериментов отмечено, что реализация БО-моделей на языке Simulink открывает хорошие перспективы модельной поддержки разработок систем управления воздухораспределением в реальных ШВС действующих шахт.

Введение

Разнообразность и сложность схем проветривания, большая длина и разветвленность вентиляционной сети, сложность получения информации о параметрах шахтной атмосферы ставят задачу управления проветриванием в ряд наиболее сложных. Система автоматического управления (САУ) расходами воздуха в шахтной вентиляционной сети (ШВС) должна осуществлять активное (изменение производительности вентиляторных установок) и пассивное (воздействие на вентиляционную струю с помощью регуляторов расхода воздуха (РРВ)) регулирование. Рассмотрим модели ШВС и САУ расходами воздуха на основе блочно-ориентированного языка моделирования.

1. Формальное описание ШВС и описание участкового РРВ

1.1 Формальное описание ШВС

Известно [1,3,4], что абстрактной математической моделью ШВС является ориентированный граф G(m, n) (рис.1), где m – количество ветвей (Q), n – количество узлов (U). Этот граф отражает топологию связей между ветвями и узлами, размещение активных элементов в сети (вентиляторов). Топология графа описывается матрицей инциденций А размерностью (m*(n-1)) и матрицей независимых контуров S (m*γ), где γ =(m-n+1).

Математическое описание переходных процессов в сети имеет вид (модель ШВС) [1,4]:

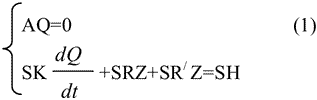
где: А – матрица инциденций;

S – матрица контуров;

Q – вектор расхода воздуха в ветвях;

R – диагональная матрица аэродинамических сопротивлений;

K – диагональная матрица аэродинамических коэффициентов;

H – вектор депрессий, создаваемых вентиляторами в ветвях;

Z – вектор с элементами Z_i = Q_i|Q_i|.

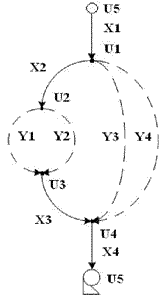
Рисунок 1 – Граф (пунктирной линией обозначены ветви антидерева, а сплошной – ветви дерева)

По методике, предложенной ранее автором в [2] составляем блочно-ориентированную (БО) модель решения системы (1), представленную на рис.2. Для разработки моделей всех объектов будем использовать средства БО-языка моделирования Simulink

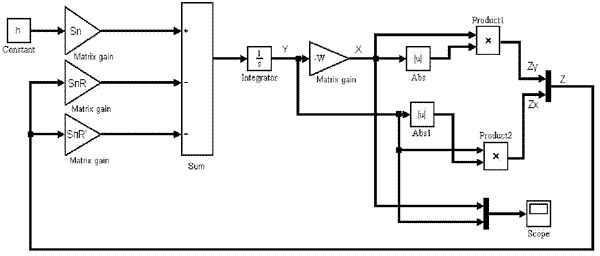
Рисунок 2 – Блочно-ориентированная модель ШВС

1.2 Система автоматического управления схем проветривания выемочных участков (СПВУ)

Так как выемочные участки являются основными объектами проветривания на угольных шахтах и в зависимости от нагрузки на них, необходимо обеспечить эти участки соответствующим количеством воздуха. Для решения задач в этой проблемной области использовалась аналогово-цифровая САУ [1,4]. Данная САУ обладает низкой степенью совместимости с современными средствами моделирования и недостаточной степенью адекватности. В связи с этим была разработана модифицированная модель САУ СПВУ.

Структура участка как объекта управления, структура системы управления потоком воздуха в ветви, а так же уравнения для каждого из звеньев системы управления предложены автором в [2]. Составим БО-модель САУ (рис.3).

Рисунок 3 – Блочно-ориентированная модель САУ

Численные значения, которые будут использоваться в процессе моделирования, представлены в таблице 1.

2. Система автоматического управления регуляторами расхода воздуха в шахтной вентиляционной сети

Поставим одну САУ в ветвь антидерева Y1, в остальных ветвях систем управления нет. На рис.3 представлена БО-модель управления расходами воздуха в ШВС. Она состоит из 3-х частей:

1. БО-модели ШВС.
2. БО-модели САУ.
3. Блока задания начальных условий.

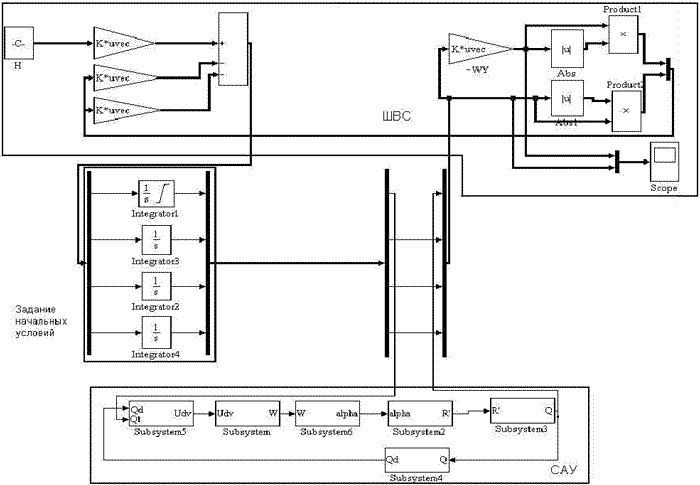
Рисунок 4 – Блочно-ориентированная модель управления расходами воздуха в ШВС

При соблюдении параметров указанных в табл. 1, при открытом РО изменение расходов воздуха в ШВС представлено на рис. 5, а. При закрытом – на рис. 5, б.

Рисунок 5 – Изменение расходов воздуха в ШВС: а – при открывании РО САУ в ветви Y1; б – при закрывании РО САУ в ветви Y1

На диаграммах отображены процессы, происходящие в ШВС при подключении к одному выемочному участку САУ. При уменьшении R^/ начинает работу двигатель, который осуществляет передвижение РО, уменьшается α, ΔQ растет и расход воздуха Q в данной ветви увеличивается. При увеличении R^/ двигатель работает в обратном режиме, α увеличивается, и расход воздуха Q уменьшается. Принцип работы САУ в ветвях Y2-Y4 будет аналогичен.

Поставим САУ во все ветви антидерева Y1-Y4.

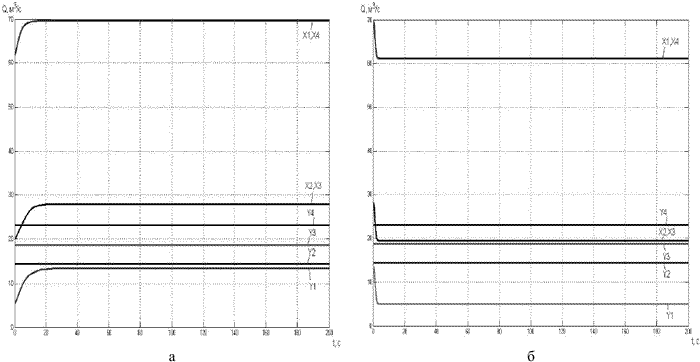
Рисунок 6 – Исследование работы САУ в ветви Y1 (с четырьмя САУ в ШВС): а – при закрывании РО САУ в ветви Y1; б – при открывании РО САУ в ветви Y1

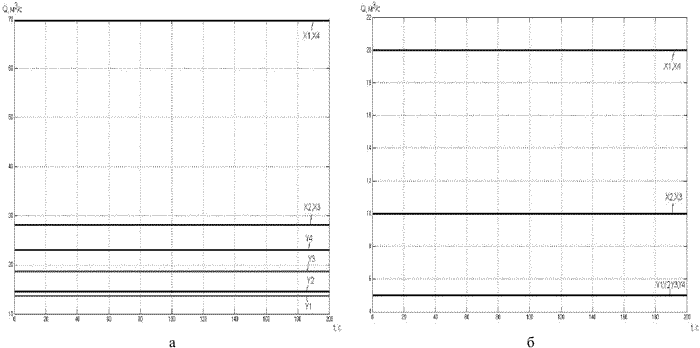
Рисунок 7 – РО во всех САУ: а – открыты; б – закрыты

При подключении САУ во все ветви антидерева будут происходить следующие процессы. При открывании РО в ветви Y1 расход воздуха Q в этой ветви увеличивается, расходы воздуха в ветвях Y2-Y4 находятся в исходном состоянии. Расходы воздуха в ветвях дерева Х1-Х4 – увеличиваются (рис.6, а). При закрывании РО в ветви Y1 расход воздуха Q в этой ветви уменьшается, расходы воздуха в ветвях Y2-Y4 остаются в исходном состоянии. Расходы воздуха в ветвях дерева Х1-Х4 – уменьшаются (рис.6, б). При одновременном изменении состояний двух или трех РО принцип изменения расходов воздуха будет такой же. Проведем еще один эксперимент. Одновременно откроем (рис.7, а) и закроем (рис.7, б) все РО, это повлечет за собой изменение расходов в ветвях дерева и стабилизирует расход воздуха в соответствующих ветвях антидерева на том уровне, на котором это требуется.

Выводы

По результатам моделирования, которые получены при разных вариантах подключения САУ в ветви ШВС и сравнения их с тестовым расчетами, можно оценить эффективность и достаточность построенной БО-модели ШВС с включенными в нее регуляторами. Результаты этих экспериментов дают возможность для исследования и разработки групповых регуляторов расхода воздуха и регуляторов вентиляторов главного проветривания.

Литература

1. Абрамов Ф. А. Моделирование динамических процессов рудничной аэрологии [Текст] / Ф. А. Абрамов, Л. П. Фельдман, В. А. Святный – Киев: Наук. думка, 1981. – 284 c.
2. Завадская Т. В. Блочно-ориентированная модель системы многосвязного управления воздухораспределением в шахтной вентиляционной сети [Текст] / Т. В. Завадская // Наукові праці Донецького національного технічного університету. Серiя Проблеми моделювання та автоматизації проектування динамічних систем (МАП-2008). – 2008. – Випуск: 7 (150). С. 104-115. ISSN 2074-7888.
3. Акутин К. Г. Управление воздухораспределением в шахтной вентиляционной сети [Текст] / К. Г. Акутин, Е. И. Филиппович, Л. А. Шойхет – Москва: Недра, 1977. – 128 с.
4. Святный В. А. Моделирование аэрогазодинамических процессов и разработка систем управления проветриванием угольных шахт [Текст] : дис. на соискание науч. степени док. техн. наук: спец. 05.13.07 Автоматизация технологических процессов и производств (промышленность) / В. А. Святный; ДПИ. – Донецк, 1985. – 440 с. – Библиогр.: с. 420-440.