Аннотация
Валерий Иванович Ознобихин, Валерий Борисович Ромодин
В статье приводятся теоретические и экспериментальные МДН в присутствие ребер на поверхности объекта и без них. Отмечается, что кромки влияют, в основном, на уровень боковых лепестков. Это влияние определяется числом излучателей, их расстоянием до ребер, а также величиной угла клина, который образует ребро. Ключевые слова: волноводно-щелевая антенна, диаграмма направленности, металлические кромки.
Введение
При размещении волноводно-щелевых антенн (ВЩА) на реальных объектах в зону излучения попадают элементы конструкции, как правило, различного рода металлические кромки, ребра. Наиболее сильно они влияют на экваториальную диаграмму направленности (ЭДН), т.е. на ДН в плоскости, перпендикулярной направлению ребер. Считается, что ребра прямолинейны и достаточно протяженны (на практике это условие часто выполняется).
В работе [1] приводятся ЭДН щелевого излучателя для часто используемых геометрий. Заметим, ЭДН одной щели достаточно хорошо описывает ЭДН всей решетки. При расчете же меридиальной ДН (МДН, диаграмма направленности в плоскости расположения ребра) нужно учитывать все щели, и влияние ребер сказывается, в основном, на уровень боковых лепестков (БЛ).
Для оценки влияния ребер на МДН рассматривается следующая задача: линейная решетка щелей, спроектированная на заданный уровень БЛ (для случая размещения на бесконечной проводящей плоскости) помещается на поверхность с ребрами и проводится численный анализ. В случае расположения антенны в пазу приводятся экспериментальные результаты.
Для численного анализа используется матричная модель ВЩА [2]. При этом внешние (собственные и взаимные) проводимости щелей рассчитываются по формуле:

На рис. 1 и 2 приведены расчетные нормированные МДН для пяти и двадцатиэлементных решеток. Поверхности, для которых проводился анализ, были: паз, с размерами А = 0.66·λ, L = 0.33·λ, α = 75° (А – размер дна паза, L – длина грани, α – угол наклона грани, λ – длина волны), широкая стенка волновода (размер стенки - 0.58·λ) и срезанный цилиндр (величина срезки - 4·λ). Сплошная кривая – ВЩА на плоскости, штриховая – в пазу, штрих пунктирная – широкая стенка волновода, пунктирная – срез цилиндра. Заметим, что в случае паза нужно учитывать 4 ребра (два внутренних и два внешних), для волновода и срезки – два ребра.
На рис. 3. приведены расчетная и измеренные МДН двадцатичетырехэлементной решетки, расположенной на плоскости (кривая 1) и в пазу с размерами А = 0.715·λ, L = 4.38·λ, α = 71°. Видно, что расчет достаточно хорошо совпадает с экспериментом.
Как показал анализ, ребра вносят систематическую ошибку в амплитуднофазовое распределение тока по щелям. Эта ошибка может на несколько градусов сдвинуть направление главного максимума, но наиболее сильно она влияет на уровень боковых лепестков. Причем это влияние тем больше, чем меньше число излучателей. Так влиянием срезки на цилиндре на МДН двадцати щелевой решетки можно пренебречь (но на ЭДН она может влиять достаточно сильно), если расстояние от щелей до ребра >λ.
Влияние ребер на МДН антенны также определяется их числом, расстоянием до излучателя и величиной угла клина, который образует ребро. Кроме того, размер решетки существенно определяет это влияние, чем меньше число излучателей, тем оно больше.
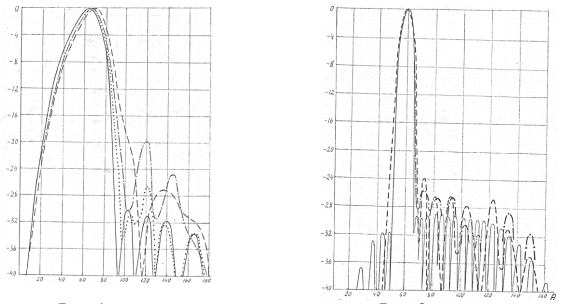
Рисунок 1, 2

Рисунок 3
Литература
- Ознобихин В.И., Стариков Е.И. Расчет ДН щелевого излучателя, расположенного на поверхности с ребрами // Информатика и проблемы телекоммуникации. Российская научнотехническая конференция. Материалы конференции. – Новосибирск: СибГУТИ, 2009. – Т. 1. – С. 96–99.
- Ознобихин В.И., Стариков Е.И. Расчет ДН щелевого излучателя, расположенного на поверхности с ребрами // Информатика и проблемы телекоммуникации. Российская научнотехническая конференция. Материалы конференции. – Новосибирск: СибГУТИ, 2009. – Т. 1. – С. 96–99.
- Ознобихин В.И., Ромодин В.Б. Расчет внешних проводимостей щелевых излучателей // Радиотехника. – М., № 2–3. – 1993.