Общая постановка проблемы
Несмотря на стремительную поступь технологий, надежные методы прикладного программирования и искусство программирования развиваются крайне медленно. Путь, позволяющий преодолеть трудности, свойственные разработке программного обеспечения, пролегает через использование подходящих методологий. В эпоху пакетной обработки безраздельно царствовали алгоритмы. Этот период можно назвать эрой «блок-схем». При построении серверных приложений, отвечающих на запросы, большую роль играет «отсутствие состояния» – нет нужды сохранять состояния между двумя последовательными запросами. При построении удачного интерактивного приложения, управляемого событиями, многое зависит от того, продумана ли модель управления состояниями.
Конечный автомат – весьма удобная концепция, которую целесообразно использовать для структурирования приложений. Продуманное применение конечных автоматов облегчает организацию и сопровождение, как логики пользовательского интерфейса, так и логики приложения. Благодаря этому код будет более гибким и надежным, причем это относится к разработке не только мобильных, но и любых других приложений. Поскольку мобильные приложения должны использовать пространство экрана и системные ресурсы эффективно, конечные автоматы оказываются особенно полезными при разработке ПО для таких приложений.
Конечный автомат, как отмечалось выше, является средством формальной структуризации приложения. Вместо того чтобы использовать все переменные приложения в качестве расширенного определения его состояния, конечный автомат создает единственную переменную, в которой хранится информация о состоянии приложения. Такой переменной обычно является элемент перечисления некоторого множества действительных состояний, определяемого глобально или на уровне класса. Мощь подхода, использующего конечные автоматы, обусловлена тем, что он позволяет в явном виде определить действительные состояния для некоторого аспекта вашего приложения и задать соответствующие варианты поведения при переходах приложения из одного состояния в другое. Конечные автоматы используются для формирования набора взаимосвязанных переменных или вариантов поведения и их логической организации, что облегчает обработку состояний.
Цель исследования
Целью данного исследования является изучение основных методов построения конечных автоматов, а также исследование основных форм представления характеристических функций конечного автомата.
Основная модель конечного автомата
Конечный автомат &ndash это некоторая абстрактная модель, содержащая конечное число состояний чего-либо. Используется для представления и управления потоком выполнения каких-либо команд. Конечный автомат идеально подходит для реализацииискусственного интеллекта в играх, получая аккуратное решение без написания громоздкого и сложного кода. В данной статье мы рассмотрим теорию, а также узнаем, как использовать простой и основанный на стеке конечный автомат.
Подобно другим теориям, развитие которых побуждается нуждами, науки и техники, теория конечных автоматов имеет дело с математическими моделями, предназначенными для приближенного отображения физических или абстрактных явлений. Значение этой теории состоит в том, что применение ее моделей не ограничивается какой-либо частной областью, а возможно непосредственно для решения проблем практически в любой области исследований от психологии до административного управления и от связи до лингвистики. Идеи и техника теории конечных автоматов используются для решения таких, казалось-бы не связанных, проблем, как исследование деятельности нервной системы человека, анализ английского синтаксиса и проектирование электронных вычислительных машин. В эпоху, когда темпы развития науки сильно зависят от межотраслевого кооперирования, унифицированный характер этой теории представляет несомненную ценность
Большинство проблем, встречающихся в науке и технике, можно разбить на следующие две категории: задачи анализа, которые состоят в предсказании поведения определенной заданной системы, и задачи синтеза, состоящие в построении системы по заданному поведению. В этой книге предпочтение будет оказано скорее задачам анализа, чем синтеза. Как с точки зрения анализа, так и с точки зрения синтеза удобно переменные, которые характеризуют систему, различать следующим образом: входные переменные, которые представляют собой воздействия, генерируемые другой системой (не подлежащей исследованию), и которые влияют на поведение исследуемой системы, выходные переменные (реакции), представляющие собой те величины, характеризующие поведение данной системы, которые интересуют исследователя, промежуточные переменные – те величины, которые не являются ни входными, ни выходными переменными.
Таблицы, графы и матрицы переходов
После того как для выбранной системы установлены входной алфавит, выходной алфавит и множество состояний, словесное описание системы может быть формализовано при помощи таблицы, графа или матрицы. Таблицы, графы и матрицы – различные формы представления характеристических функций конечного автомата, который описывает данную систему (рис. 1).
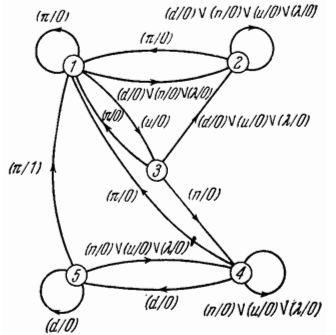
Рис. 1 – Граф перехода
Такое представление совершенно необходимо для проведения любого точного анализа или синтеза конечного автомата, и мы будем им широко пользоваться в настоящей книге. Поскольку одной формой представления автомата выгодно пользоваться при одних обстоятельствах, другой – при других, полезно познакомиться со всеми формами представления.
Одним из важных применений таблицы переходов является использование ее для перечисления автоматов, принадлежащих тому или иному классу. Класс автоматов часто может быть определен при помощи ряда ограничений, накладываемых на распределение состояний и выходных символов в таблице переходов. Заданный класс автоматов может быть перечислен путем построения всех возможных таблиц переходов, удовлетворяющих этим ограничениям. Часто мощность класса может быть сразу оценена путем подсчета определяемого заданными ограничениями числа степеней свободы при построении таблиц переходов.
Недетерминированный конечный автомат
Недетерминированный конечный автомат – абстрактная машина, которая читает символы из входной цепочки и решает, допустить или отвергнуть эту цепочку. Он может изменить состояние, перейдя из одного состояния в другое. Внутреннюю структуру такого автомата можно представить графом переходов НКА тоже распознаёт цепочки символов, цепочка считается допустимой, если после её обработки множество состояний, в котором оказался автомат, содержит хотя бы одно допускающее. Таким образом, НКА также задаёт некоторый язык.
Любой недетерминированный конечный автомат может быть преобразован в детерминированный так, чтобы их языки совпадали и такие автоматы называются эквивалентными. Однако, поскольку количество состояний в эквивалентном ДКА в худшем случае растёт экспоненциально с ростом количества состояний исходного НКА, на практике подобная детерминизация не всегда возможна. Кроме того, конечные автоматы с выходом в общем случае не поддаются детерминизации.
Для каждого состояния и каждого входного символа НКА имеет ноль или более вариантов выбора следующего шага. Он может также выбирать, сдвигать ему входную головку при изменении состояния или нет. Приведем определение недетерминированного конечного автомата.
С каждым НКА связан ориентированный граф, естественным образом представляющий функцию переходов этого автомата.
Приведем определение для графа (или диаграммы) переходов автомата М = (S, I, a, s, F). Графом переходов автомата М называют ориентированный граф G = (S, E) с помеченными ребрами (рис. 2

Рис. 1 – Пример НКА
Существует дополнительный результат или возможность сопоставить какому-либо взятому НКА эквивалентную «детерминированную» машину. Однако детерминированный конечный автомат, эквивалентный данному НКА с n состояниями, может иметь вплоть до 2 в n степени состояний. Поэтому переход от НКА к детерминированному автомату не всегда дает эффективный способ моделирования недетерминированного конечного автомата.
Выводы
Идея применения конечных автоматов является чрезвычайно полезной концепцией, плодотворность которой прошла проверку временем. Использование конечных автоматов позволяет разработчикам создавать хорошо организованные приложения с гибкими возможностями. Их применение позволяет создавать ясный, понятный и надежно функционирующий код.
Были изучены основные методы построения конечных автоматов, исследованы основные формы представления характеристических функций конечного автомата.
Список использованной литературы
- Автоматное управление асинхронными процессами в ЭВМ и дискретных системах / Под. ред. В. И. Варшавского. – М. : Наука, 2006. – 400 с.
- Крючкова, Е.Н. Теория формальных языков и автоматов / Е.Н. Крючкова – М. : Наука, 2008. – 225 с.
- Донован, Дж. Системное программирование / Дж. Донован. – М. : Мир, 1975. – 540 с.
- Горбунов, А.Н. Синтез конечного распознающего автомата / Методические указания к выполнению дипломной работы. / А.Н. Горбунов. – Брянск : Мир, 2004. – 20 с.
- Поспелов, Д.А. Логические методы анализа и синтеза схем / Д.А. Поспелов. – СПб. : Энергия, 1974. – 368 с.
- Гилл А. Введение в теорию конечных автоматов / А. Гилл – М. : Наука, 1966. – 272 с