Исследование стационарной конвективной математической модели кристаллизации вещества

Аннотация

Миненко А.С. Исследование стационарной конвективной математической модели кристаллизации вещества. Исследуется стационарная задача Стефана с учётом конвективного движения в жидкой фазе на плоскости. Получено уравнение свободной границы в зависимости от интенсивности вихря. Строится приближенное решение задачи.

Постановка задачи

Математическое моделирование теплофизических процессов в спецметаллургии оперирует такими усредненными величинами, как понятие сплошной среды, её плотность, теплоемкость, температуро- и теплопроводность, вязкость и др., и, опираясь на законы переноса массы, импульса и энергии, составляют основные дифференциальные уравнения для определения других усредненных характеристик - векторного поля скоростей, температурного поля и др. Все теплофизические параметры среды в той или иной степени зависят от температуры, а законы, управляющие этими зависимостями, носят экспериментально-эмпирический характер и до настоящего времени весьма неполны, особенно в области высоких температур, поэтому поневоле приходится рассматривать линейное приближение, применимое в случае малых перепадов температуры, когда зависимостью упомянутых параметров от термодинамического состояния можно пренебречь. Адекватность математической модели физическому явлению возрастает вместе с уточнением упомянутых зависимостей, вследствие чего еще большее значение приобретают соответствующие эксперименты общепознавательного характера. Линеаризованная теория задач массо- и теплопереноса оперирует также с известным количеством безразмерных параметров изучаемого явления, таких, как числа Рейнольдса, Пекле, Нуссельта, Прандтля и др., и значение этих параметров для возможно большего диапазона материалов и режимов тоже приобретает повышенное значение.

Теплофизические процессы в кристаллизаторе, сопровождающиеся фазовыми переходами вещества, описываются математической моделью, в которой температура каждой из фаз удовлетворяет уравнению переноса тепла со своими теплофизическими коэффициентами. На границе раздела фаз обе температуры постоянны и равны температуре фазового перехода (для химической однородной среды), а на заданных частях границы, – стенках кристаллизатора, поддоне, – поддерживается определенный режим (теплоотвод, теплоизоляция и др.). Поверхность раздела фаз (фронт кристаллизации) является неизвестной, или «свободной» границей, и для ее определения дополнительно задается «условие Стефана», означающее, что тепловой поток через фронт кристаллизации в сторону твердой фазы равен тепловому потоку со стороны жидкой фазы плюс скрытая теплота фазового перехода. Жидкая фаза рассматриваемого процесса заслуживает специального исследования из-за априорной возможности существования поля скоростей, вызывающего интенсивную теплопередачу путем конвекции. Усиленная циркуляция в расплавленной шлаковой ванночке была обнаружена в исследованиях академика Б.Е. Патона и его сотрудников [1].

Основной целью настоящей статьи является изучение гидродинамических явлений в жидкой фазе, поскольку здесь экспериментальные исследования, насколько известно, отсутствуют.

Изучается стационарный случай в полосе D = {–1 < x < 1 H < y < 0}. Обозначим через γ кривую, отделяющую жидкую фазу D_γ⁺ от твердой D_γ^–, при этом концы γ лежат на вертикалях x = ±1. Обе области D_γ⁺ и D_γ^– предполагаются односвязными и симметричными относительно оси y. Пусть ψ(x, у) – функция тока, удовлетворяющая условиям: Δψ = μ, (x, у)∈D_γ⁺, μ = const > 0, ψ = 0 (x, у)∈∂D_γ⁺. Здесь μ считается достаточно малым численным параметром. Требуется определить, кроме функции тока ψ(x, у), тройку (u^±(x, у), γ) по следующим условиям:

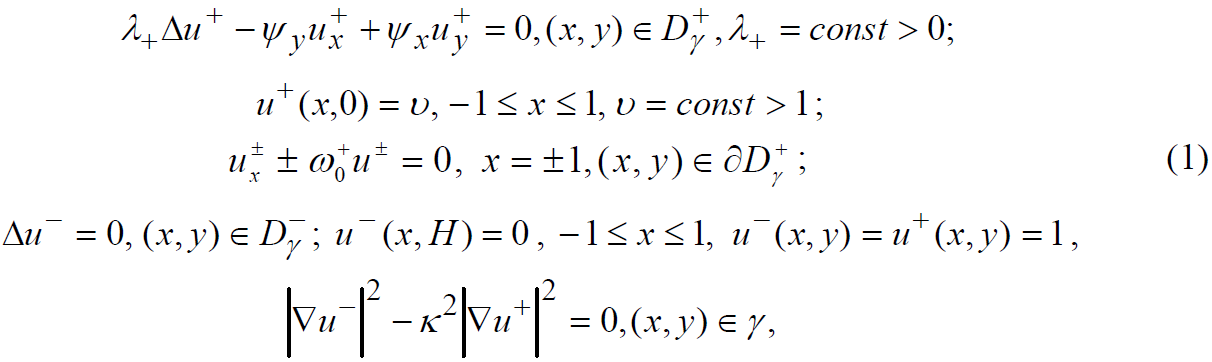
здесь k = const, 0 < k ≤ 1; ω₀^± – числа Нусельта.

Приближенное решение задачи

Предложен метод изучения нелинейной задачи (1), состоящий в разложении решения в ряд по степеням малого параметра μ [2]:

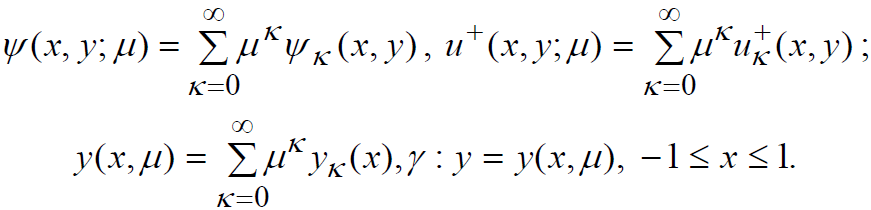
Нулевое приближение u₀(x, у) ищем как минимум функционала

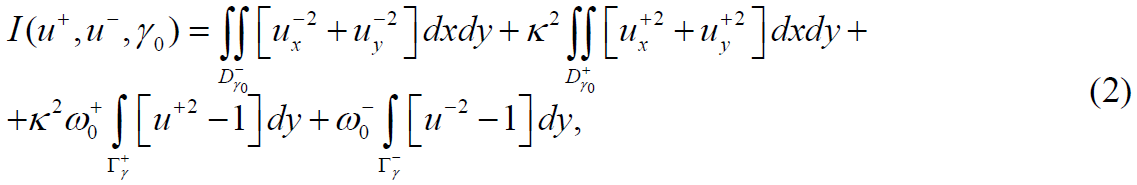
на соответствующем множестве допустимых функций, здесь Г_γ⁺ = ∂D_γ⁺∩{x = ±1}, Г_γ^– = ∂D_γ^–∩{x = ±1}. Функционал (2) в классе функций u₀^± в D_γ^± представим следующим образом:

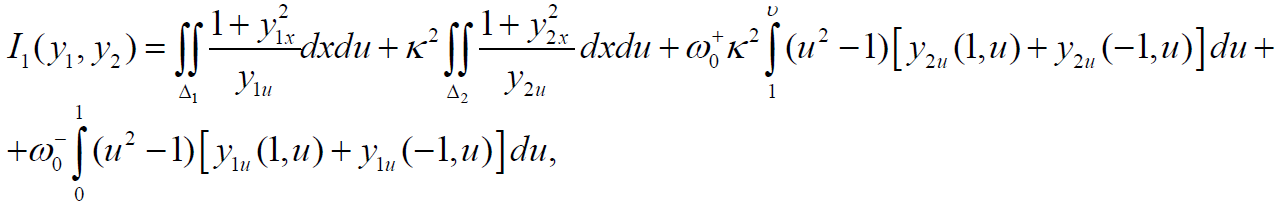
где Δ₁ = (–1 < x < 1, 0 < u < 1), Δ₂ = (–1 < x < 1, 1 < u < ϑ), y₁(x, u) и y₂(x, u) – решения уравнений u₁(x, у) – u₁ = 0, u₂(x, у) – u₂ = 0.

Будем минимизировать функционал I₁(y₁, y₂) при помощи сумм

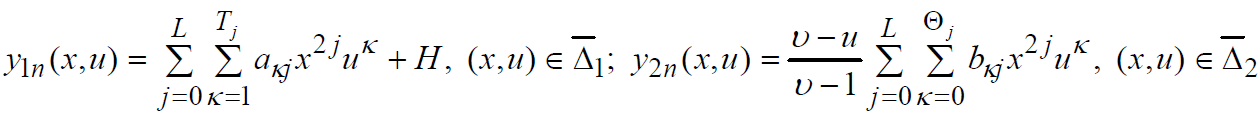
применяя при этом метод Ритца [3]:

Лемма. Пусть система Ритца (3) имеет решение при некоторых значениях параметров . Тогда решения этой системы a_kj (ω⁺, ω₀^–, k), b_kj (ω₀⁺, ω₀^–, k) непрерывно зависят от параметров ω⁺, ω₀^–, k в некоторой окрестности точки .

Проблема сходимости приближенных решений исследована в [3], [4].

Теорема. Пусть μ достаточно малая величина. Тогда справедлива формула:

где y₀ (x) – решение уравнения u₀(x, у) – 1 = 0 в классе функций u_0y(x, у) > 0 в D; u₁(x, у) – решение краевой задачи:

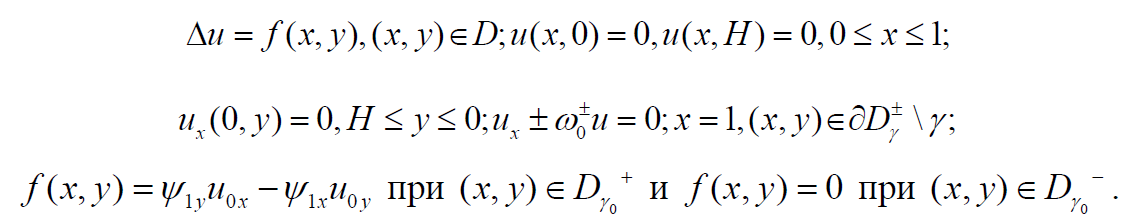
Приближенный анализ влияния конвекции на фронт кристаллизации

Численный анализ осуществлялся на основании формулы (4). В качестве функции u₀(x, у) берется решение проблемы минимума функционала (2), которое может быть построено методом Фурье при k = 1, ω₀⁺ = ω₀^– = ω₀. Функции ψ₁(x, у) и u₁(x, у) находятся из условий минимума функционалов

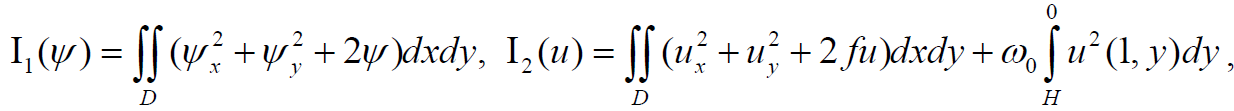
на множествах

Проблема минимума эффективно решается при помощи метода Ритца. При этом приближения Ритца ψ_n и u_n строятся следующим образом:

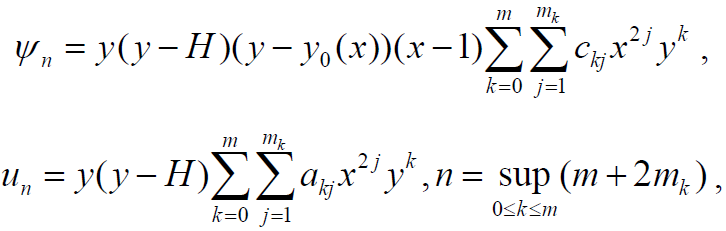
где y₀ (x) – решение уравнения u₀(x, у) – 1 = 0, (x, у) ∈ D в классе функций u_0y(x, у) > 0 в D. Сходимость приближенных решений к точным решениям, соответствующих краевых задач, изучена в [5]. Неизвестные коэффициенты a_kj и c_kj – определяются из условий минимума функций .

Численный эксперимент осуществлялся при определенных значениях теплофизических значений параметров. На рис. 1 изображен график линий кристаллизации у(х, μ) при различных значениях μ, соответственно при μ = –0,5; 0; 0,1; 0,5. Кривые у(х, μ) строились в виде многочленов

Вычисления производились при Н = –10, ν = 1,25, ω₀ = 3,5, при этом y₁ = y(x;0,5); y₂ = y(x;0,1); y₄ = y(x;–0,5) и y₃ = y₀(x).

Проделанный численный эксперимент подтверждает влияние конвективного теплообмена на процесс кристаллизации. Эксперимент сохранит свой смысл, если параметры ω₀⁺ и ω₀^– брать в некоторой малой окрестности чисел ω₀ = 3,5, а k = 1.

Литература

1. Патон Б.Е. Избранные труды / Патон Б.Е. – Киев : ТР. ИЭС им. Е.О. Патона НАН Украины, 2008. – 893 с.
2. Миненко А.С. Вариационные задачи со свободной границей / Миненко А.С. – Киев : Наукова думка, 2005. – 341 с.
3. Миненко А.С. Исследование одной конвективной задачи Стефана методом Ритца / А.С. Миненко // Укр. мат. журнал. – 2007. – 59, № 11. – С. 1546–1556.
4. Миненко А.С. О минимизации одного интегрального функционала методом Ритца / А.С. Миненко // Укр. мат. журнал. – 2006. – 58, № 10. – С. 1385–1394.
5. Харик И.Ю. О проблеме аппроксимации функций, связанной с исследованием сходимости вариа-ционных процессов / И.Ю. Харик // Докл. АН СССР. – 1951. – 81, № 2. – С. 157–160.