Аннотация
Шевченко А.И., Миненко А.С., Сыпко И.А. Моделирование одного класса сложных систем с нечетким управлением. Исследуется одна задача Стефана с учетом конвекции в жидкой фазе. Построено приближенное решение этой задачи с использованием малого параметра. Управление этим процессом осуществляется с применением нечеткой логики.
Постановка задачи
Рассмотрим следующий вариант кристаллизации металла. Пусть полубесконечный круговой цилиндр Ω = {(x1, x2, x3): x12 + x22 < R2, x3 < 0} заполнен веществом, которое находится в двух фазовых состояниях: твердом и жидком. В рассматриваемой модели теплофизические параметры (свои в каждой фазе) считается постоянными величинами. Пусть, далее Гt – достаточно гладкая поверхность, граничные точки которой S лежат на Г – боковой поверхности цилиндра Ω, т.е. S ∈ Г, и пусть Гt отделяет твердую фазу от жидкой. Область, заполненную жидким веществом обозначим через Ωt+. Через Ωt– обозначим область занятую твердым веществом. Боковые границы этих областей обозначим соответственно через Г– и Г+. Верхний участок границы цилиндра Ω обозначим через H. Рассмотрим случай, когда каждая фаза Ωt± представляет собой односвязную область и для каждого момента времени t > 0 не является пустым множеством. Двухфазная задача Стефана, при наличии конвективных движений в жидкой фазе, состоит в определении скорости жидкости ![]() , распределения температур u+(x, t) и u–(x, t) соответственно в жидкой и твердой фазах, свободной поверхности Гt и давления p(x, t) по следующим условиям:
, распределения температур u+(x, t) и u–(x, t) соответственно в жидкой и твердой фазах, свободной поверхности Гt и давления p(x, t) по следующим условиям:
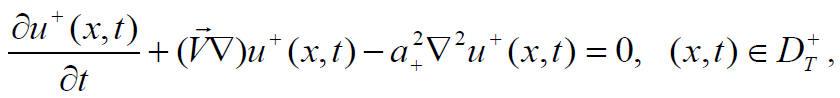

где DT±(x, t): x ∈ Ωt±, t ∈ (0, T), x = (x1, x2, x3), ω0±, Re, k, k–, k+ – заданные положительные константы, q(х) – известная положительная, достаточно гладкая функция, ∇ = (∂/∂x1, ∂/∂x2, ∂/∂x3). Здесь также a+2 = λ+/Re–ρ+, a–2 = λ–/Re–ρ–, а λ±, c±, ρ± – известные теплофизические параметры. Предполагается, что ![]() ,
, ![]() ,
, ![]() , q(x) ∈ H2+α, где Ω0± – области со свободной границей Г0, которые возникают при рассмотрении стационарной задачи без конвекции с теми же условиями из (1) при Rе = 0.
, q(x) ∈ H2+α, где Ω0± – области со свободной границей Г0, которые возникают при рассмотрении стационарной задачи без конвекции с теми же условиями из (1) при Rе = 0.
Задача (1) моделирует процесс кристаллизации металла при электрошлаковом переплаве с учетом конвективного переноса тепла, реально присутствующем в жидкой фазе. Наконец, разрешимость класса задач типа (1) в пространстве ![]() изложена в [1].
изложена в [1].
Приближенные решения задачи (1). Введем криволинейные координаты ω = (ω1, ω2) для точек поверхности Г0 и будем искать поверхность Гt в следующем виде: ![]() , где ρ(ω, t) – функция класса
, где ρ(ω, t) – функция класса ![]() – нормаль к Г0, направленная внутрь Ω0+, x(ω) ∈ Г0 [2, 3].
– нормаль к Г0, направленная внутрь Ω0+, x(ω) ∈ Г0 [2, 3].
Предположим, что решения задачи (1) можно разложить в ряд по степеням Re: 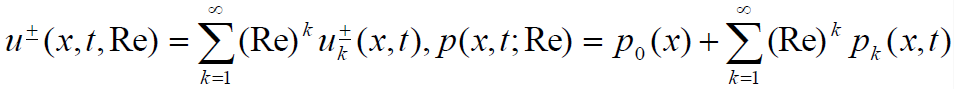 ,
,  .
.
Справедливы утверждения.
Лемма. Пусть выполнены условия: ∇2A±(x) = 0, x ∈ Ω0±, 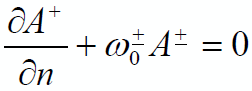 ,
, 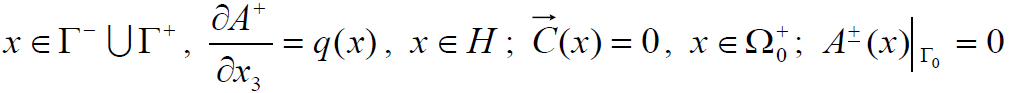 и k–|∇A–(x)| = k+|∇A+(x)| на Г0. Тогда в качестве нулевого приближения u0±(x) можно взять функции A±(x), а свободная поверхность Г0 принадлежит классу C∞ каждой точке, лежащей внутри цилиндра Ω.
и k–|∇A–(x)| = k+|∇A+(x)| на Г0. Тогда в качестве нулевого приближения u0±(x) можно взять функции A±(x), а свободная поверхность Г0 принадлежит классу C∞ каждой точке, лежащей внутри цилиндра Ω.
Теорема. Пусть выполнены условия леммы и пусть справедливы соотношения: ∇p0(x) = 0, ∇p1(x, 0) = 0, x ∈ Г0 и c(k+ + k–)T/k < 1 где с – некоторая постоянная [4, с.364], тогда существуют первые приближения u1±(x, t), ![]() , p1(ω, t) и u2±(x, t),
, p1(ω, t) и u2±(x, t),![]() , p2(ω, t) задачи (1), причем функции u1±(x, t) и u1±(x, t) принадлежат классу
, p2(ω, t) задачи (1), причем функции u1±(x, t) и u1±(x, t) принадлежат классу ![]() , а ρ1(ω, t) и ρ2(ω, t) –
, а ρ1(ω, t) и ρ2(ω, t) – ![]() . И кроме того при малых числах Rе и достаточно малых значениях t справедлива формула Гt:
. И кроме того при малых числах Rе и достаточно малых значениях t справедлива формула Гt:

Нечеткое управление процессом кристаллизации. Пусть u* – температура, которую должна достичь поверхность ∂Ω = Г∪H. Данная задача возникает в спецметаллургии при отделении выплавленного слитка от стенок кристаллизатора [5]. Эта температура достигается за счет воздействия тепловых потоков мощности w1, w2, w3, причем поток w3 равномерно распределен в центре H, а два других потока w1, w2 сконцентрированы по краям Г∪H. Далее предлагается метод нечеткого управления в данном классе задач.
Пусть X1, X2, ...Xn – факторы, влияющие на процесс кристаллизации, а Y1, Y2, ...Yn – условия, при которых происходит появление нового слитка. Тогда нечеткое управление в нашей задаче представляется в виде функционального отображения: X = {X1, X2, ...Xn} → Y = {Y1, Y2, ...Yn}.
Ради простоты, в качестве терм-множества лингвистических переменных x1, x2, x3, где x1 = {"температура"}, x2 = {"способ нагрева"}, x3 = {"слиток металла"} будем использовать множества: T = {"минимальная", "средняя", "максимальная"}, W = {"минимальный", "средний", "максимальный"}, L = {"минимальный", "средний", "максимальный"}.
Таким образом, имеем: x = {x1, x2, x3}→y ∈[α,β], где α и β – некоторые числа (они выбираются таким образом, чтобы произошло отделение слитка от стенок кристаллизатора [5]), а для выходной лингвистической переменной У (температура поверхности слитка) будет использоваться терм-множество Q = {"минимальная", "средняя", "максимальная"}. Для численной реализации задачи использовались следующие значения параметров [5]): 400мм ≤ L ≤ 6000мм, 2500МБт/м2 ≤ W ≤ 5000МВт/м2. Численный расчет, позволяющий построить графически нечеткое управление, был осуществлен с помощью стандартного алгоритма Мамдани.
Замечания. Приближенное решения класса задач типа (1) изложено в [6] и [7].
Литература
- Шевченко А.И., Миненко А.С. Методы исследования нелинейных моделей, – Киев: Наук.думка, 2012. – 132 с.
- Миненко А.С. Вариационные задачи со свободной границей / Миненко А.С. – Киев : Наукова думка, 2005. – 341 с.
- Шевченко А.И., Миненко А.С. Задача Стефана при наличии конвекции // Доп. НАН України. – 2012. – № 1. – С. 25–29.
- Ладыженская О.А., Салонников В.А., Уральцева Н.Н. Линейные и квазилинейные уравнения параболического типа. – Москва: Наука, 1967 – 756 с.
- Патон Б.Е. Избранные труды. – Киев: Институт электросварки им.Е.О.Патона НАН Украины, 2008. – 893 с.
- Шевченко А.И., Миненко А.С. Приближенный анализ стационарной конвективной задачи Стефана// Доп. НАН України. – 2010. – № 5. – С. 36–40.
- Шевченко А.И., Миненко А.С., Золотухина О.А. Численный анализ одной нелинейной математической модели // Доп. НАН України. – 2012. – № 9. – С. 44–47.