Аннотация
Термин глубокое обучение
или глубокая нейронная сеть
относится к искусственным нейронным
сетям (ИНС) с несколькими уровнями. В течение последних нескольких десятилетий он считался одним из самых мощных инструментов и стал очень популярным в
литературе, поскольку он может обрабатывать огромное количество данных. Интерес к более глубоким скрытым слоям в последнее время стал превосходить
классические методы в различных областях; особенно в распознавании образов. Одна из самых популярных глубоких нейронных сетей - сверточная нейронная сеть
(СНС). Это название произошло от математической линейной операции между матрицами, называемой сверткой. СНС имеют несколько уровней; включая сверточный слой,
слой нелинейности, слой пулинга и полносвязный слой. Сверточные и полносвязные слои имеют параметры, но слои пулинга и нелинейности не имеют параметров.
СНС отлично справляется с задачами машинного обучения. Особенно приложения, которые имеют дело с данными изображений, такими как самый большой набор данных
классификации изображений (ImageNet), компьютерное зрение и обработка естественного языка (NLP), и достигнутые результаты были очень удивительными. В этой
статье мы объясним и определим все элементы и важные вопросы, связанные с СНС, и то, как эти элементы работают. Кроме того, мы также укажем параметры,
влияющие на эффективность СНС. В этой статье предполагается, что читатели обладают достаточными знаниями как о машинном обучении, так и об искусственных
нейронных сетях.
Введение
Сверточная нейронная сеть за последнее десятилетие добилась новаторских результатов в различных областях, связанных с распознаванием образов; от обработки изображений до распознавания голоса. Самый выгодный аспект СНС - это уменьшение количества параметров в ИНС. Это достижение побудило как исследователей, так и разработчиков использовать более крупные модели для решения сложных задач, что было невозможно с классическими ИНС. Самое важное предположение о проблемах, которые решает СНС, не должно иметь пространственно зависимых признаков. Другими словами, например, в приложении для обнаружения лиц нам не нужно обращать внимание на то, где на изображениях расположены лица. Единственная забота - обнаружить их независимо от их положения на данных изображениях. Другой важный аспект СНС - получение абстрактных признаков при распространении входных данных на более глубокие слои. Например, при классификации изображений край может быть обнаружен в первых слоях, затем более простые формы во вторых слоях, а затем элементы более высокого уровня, такие как лица в следующих слоях, как показано на рис. 1 и в [1, 3, 5, 15].
Элементы сверточной нейронной сети
Чтобы получить хорошее представление о СНС, мы начнем с его основных элементов..
Свертка
Предположим, что вход нашей нейронной сети имеет форму, представленную на рис. 2. Это может быть изображение (например, цветное изображение набора данных CIFAR-10 с шириной и высотой 32x32 пикселя и глубиной 3 RGB канала) или видео (видео в градациях серого, высота и ширина которого являются разрешением, а глубина - кадрами) или даже экспериментальное видео, ширина и высота которого соответствуют значениям датчика (LxL), а глубины связаны с разными временные рамки, как в [2, 10, 15].
Почему свертка? Предположим, что сеть получает на вход пиксели. Следовательно, чтобы подключить входной слой только к одному нейрону (например, в скрытом слое в многослойном персептроне), в качестве примера, должны быть весовые соединения 32x32x3 для набора данных CIFAR-10.

Рисунок 1 - Изученные признаки сверточной нейронной сети

Рисунок 2 - Трехмерное входное представление СНС
Если мы добавим еще один нейрон в скрытый слой, то нам понадобится еще одно весовое соединение 32x32x3, которое в сумме станет параметрами 32x32x3x2. Чтобы было понятнее, используется более 6000 весовых параметров для подключения входа только к двум узлам. Можно подумать, что двух нейронов может быть недостаточно для какой-либо полезной обработки в приложении для классификации изображений. Чтобы сделать его более эффективным, мы можем подключить входное изображение к нейронам в следующем слое с точно такими же значениями для высоты и ширины. Можно предположить, что эта сеть применяется для такого типа обработки, как края изображения. Однако для упомянутой сети требуются соединения с весом 32x32x3 на 32x32, что составляет (3145728), как в [4, 5, 14].
Поэтому в поисках более эффективного метода выяснилось, что вместо полного соединения рекомендуется искать локальные области на картинке, а не на всем изображении. На рис. 3 показано региональное соединение для следующего уровня. Другими словами, скрытые нейроны в следующем слое получают входные данные только из соответствующей части предыдущего слоя. Например, он может быть подключен только к нейронам 5x5. Таким образом, если мы хотим иметь 32x32 нейрона в следующем слое, то у нас будет 5x5x3 на 32x32 соединения, что составляет 76800 соединений (по сравнению с 3145728 для полного соединения), как в [1, 9, 13, 14, 17].
Хотя размер соединения резко упал, остается решить еще очень много параметров. Другое предположение для упрощения - сохранить фиксированные веса локальных соединений для всех нейронов следующего слоя. Это соединит соседние нейроны в следующем слое с точно таким же весом с локальной областью предыдущего слоя. Следовательно, он снова отбрасывает множество дополнительных параметров и уменьшает количество весов до 5x5x3 = 75, чтобы соединить нейроны 32x32x3 с 32x32 на следующем слое [5, 8, 11].
У этих простых предположений есть много преимуществ. Во-первых, количество подключений уменьшилось с 3 миллионов до 75 в представленном примере. Во-вторых, что более интересно, фиксация весов для локальных подключений аналогична перемещению окна 5x5x3 во входных нейронах и отображению сгенерированного выхода в соответствующее место. Это дает возможность обнаруживать и распознавать особенности независимо от их положения на изображении. По этой причине их называют свёрткамии [6, 7, 16].
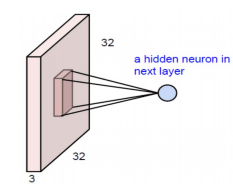
Рисунок 3 - Свертка как альтернатива для полносвязной сети
Чтобы продемонстрировать поразительный эффект матрицы свертки, на рис.4 показано, что произойдет, если мы вручную выберем вес соединения в окне 3x3.
Как мы видим на рисунке 4, матрица может быть настроена на обнаружение краев изображения. Эти матрицы также называются фильтрами, потому что они действуют как классические фильтры при обработке изображений. Однако в сверточной нейронной сети эти фильтры инициализируются, за ними следуют фильтры формы процедуры обучения, которые больше подходят для данной задачи.
Чтобы сделать этот метод более эффективным, можно добавить дополнительные слои после входного слоя. Каждый слой может быть связан с разными фильтрами. Таким образом, мы можем извлекать из данного изображения различные признаки. На рис. 5 показано, как они связаны с разными слоями. Каждый слой имеет свой собственный фильтр и поэтому извлекает из входных данных разные признаки. Нейроны, показанные на рис. 5, используют другой фильтр, но смотрят на одну и ту же часть входного изображения. [6, 8, 15, 17]
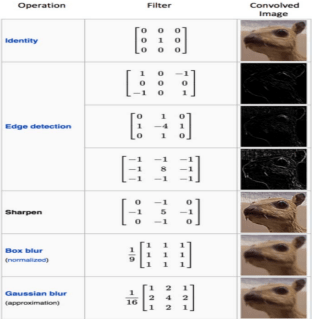
Рисунок 4 - Эффекты различных матриц свертки
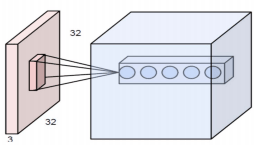
Рисунок 5 - Несколько слоев, каждый из которых соответствует разному фильтру, но смотрит на одну и ту же область на данном изображении
Шаг
Фактически, у СНС есть больше возможностей, которые предоставляют множество возможностей даже для все большего и большего уменьшения параметров и в то же время для уменьшения некоторых побочных эффектов. Один из таких вариантов - шаг. В вышеупомянутом примере просто предполагается, что узел следующего уровня имеет много перекрытий со своими соседями, глядя на регионы. Мы можем управлять перекрытием, контролируя шаг. На рис. 6 показано заданное изображение 7x7. Если мы каждый раз перемещаем фильтр на один узел, мы можем получить только выход 5x5. Обратите внимание, что выходные данные трех левых матриц на рис. 6 перекрываются (и три средние вместе, и три правые также). Однако, если мы переместимся и сделаем каждые 2 шага, то результат будет 3x3. Проще говоря, не только перекрытие, но и размер вывода будет уменьшен. [5, 12, 16].
Формула (1) формализует это, учитывая размер изображения NxN и размер фильтра FxF, выходной размер O, как показано на рисунке 7.

Где N - размер ввода, F - размер фильтра, а S - размер шага.
Заполнение
Одним из недостатков этапа свертки является потеря информации, которая может происходить на границе изображения. Поскольку они фиксируются только тогда, когда фильтр скользит, у них никогда не будет возможности увидеть. Очень простой, но эффективный способ решить проблему - использовать заполнение нулями. Другое преимущество нулевого заполнения - это управление размером вывода. Например, на рис. 6 при N = 7 и F = 3 и шаге 1 результат будет 5x5 (который сокращается по сравнению с входом 7x7).

Рисунок 6 - Шаг 1, окно фильтра перемещается только один раз для каждого соединения
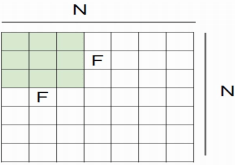
Рисунок 7 - Эффект шага на выходе
Однако при добавлении одного заполнения нулями на выходе будет 7x7, что в точности совпадает с исходным размером (фактическое N теперь становится 9, используйте формулу (1). Модифицированная формула, включающая заполнение нулями, является формулой (2).

Где P - это количество слоев нулевого заполнения (например, P = 1 на рис. 8), эта идея заполнения помогает нам предотвратить уменьшение размера сетевого вывода с увеличением глубины. Следовательно, возможно иметь любое количество глубоких сверточных сетей. [2, 12]
Особенность СНС
Разделение веса вносит в модель переводы на инвариантность. Это помогает отфильтровать элемент обучения независимо от пространственных свойств. Запуская случайные значения для фильтров, они научатся определять границу (например, на рис. 4), если это улучшает производительность. Важно помнить, что если нам нужно знать, что что-то пространственно важно в данном вводе, то использовать общий вес - крайне плохая идея.

Рисунок 8 - Нулевое заполнение

Рисунок 9 - Визуализация сверточных глубоких слоев нейронной сети
Эта концепция также может быть расширена на другие измерения. Например, если это последовательные данные, такие как аудио, тогда он может использовать одномерный звук. Если это изображение, как показано, могут применяться двухмерные свертки. А для видео или 3D-изображений можно использовать трехмерную свертку. Эта простая идея превзошла все классические методы распознавания объектов в компьютерном зрении в конкурсе ImageNet 2012 года, как показано на рис. 9, [5, 14, 18]
Сверточная формула
Свертка для одного пикселя в следующем слое рассчитывается по формуле (3).
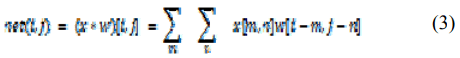
Где net(i,j) - это выход на следующем уровне, x - входное изображение, w - матрица ядра или фильтра, а * - операция свертки. Рис. 10 показывает, как работает свертка. Как можно видеть, поэлементное произведение входных данных и ядра агрегируется, а затем представляет соответствующую точку на следующем уровне. [4, 9]
Нелинейность
Следующий слой после свертки - нелинейный. Нелинейность можно использовать для регулировки или отключения генерируемого вывода. Этот слой применяется для насыщения вывода или ограничения генерируемого вывода.
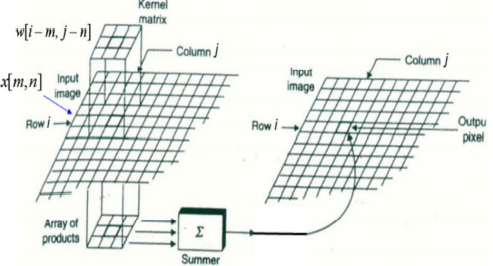
Рисунок 10 - Детали слоя свертки
В течение многих лет сигмовидная и тангенциальная формы были самыми популярными нелинейностями. На рис. 11 показаны распространенные типы нелинейности. Однако в последнее время Rectified Linear Unit (ReLU) стал использоваться все чаще по следующим причинам.
- ReLU имеет более простые определения как функции, так и градиента.

- Функция насыщения, такая как сигмовидная и tanh, вызывает проблемы при обратном распространении. По мере того, как конструкция нейронной сети становится
глубже, сигнал градиента начинает исчезать, что называется
исчезающим градиентом
. Это происходит потому, что градиент этих функций очень близок к нулю почти везде, кроме центра. Однако ReLU имеет постоянный градиент для положительного входа. Хотя функция не является дифференцируемой, в реальной реализации ее можно игнорировать. - ReLU создает более разреженное представление. Потому что ноль в градиенте приводит к получению полного нуля. Однако сигмовидная и tanh всегда имеют ненулевые результаты от градиента, что может не подходить для обучения. [2, 5, 13]

Рисунок 11 - Распространенные типы нелинейности
Пулинг
Основная идея пулинга - это понижающая дискретизация, чтобы упростить последующие слои. В области обработки изображений это можно рассматривать как уменьшение разрешения. Пулинг не влияет на количество фильтров. Максимальный пулинг - один из наиболее распространенных методов пулинга. Он разбивает изображение на прямоугольники подобласти и возвращает только максимальное значение внутренней части этой подобласти. Один из наиболее распространенных размеров, используемых в макс-пулинге, - 2x2. Как видно на рис. 12, когда пулинг выполняется в верхнем левом блоке 2x2 (розовая область), он перемещается на 2 и фокусируется на верхней правой части. Это означает, что шаг 2 используется при объединении. Чтобы избежать понижающей дискретизации, можно использовать шаг 1, что встречается нечасто. Следует учитывать, что понижающая дискретизация не сохраняет положение информации. Следовательно, его следует применять только тогда, когда важно наличие информации (а не пространственной информации). Более того, объединение может использоваться с неравными фильтрами и шагами для повышения эффективности. Например, макс-пулинг 3x3 с шагом 2 сохраняет некоторые перекрытия между областями. [5, 10, 16]

Рисунок 12 - Демонстрируется макс-пулинг. Максимальное объединение с фильтром 2x2 и шагом 2, приводящим к понижающей дискретизации каждого блока 2x2, отображается в 1 блок (пиксель).
Полносвязный слой
Полносвязный слой похож на то, как нейроны расположены в традиционной нейронной сети. Следовательно, каждый узел в полностью подключенном уровне напрямую подключен к каждому узлу как на предыдущем, так и на следующем уровне, как показано на рисунке 13. Из этого рисунка мы можем отметить, что каждый из узлов в последних кадрах в слое пулинга связаны как вектор с первым слоем из полносвязного слоя. Это наиболее часто используемые параметры СНС на этих слоях, и для их обучения требуется много времени. [3, 8].
Главный недостаток полносвязного слоя заключается в том, что он включает множество параметров, которые требуют сложных вычислений в обучающих примерах. Поэтому мы стараемся исключить количество узлов и соединений. Удаленные узлы и соединение могут быть выполнены с помощью метода выпадения. Например, LeNet и AlexNet разработали глубокую и широкую сеть, сохранив при этом вычислительную сложность постоянной. [4, 6, 9].
Суть сети СНС, которая является сверткой, состоит в том, что вводятся нелинейность и слой пулинга. Наиболее распространенная архитектура использует три из них как

Рисунок 13 - Полносвязный слой
Популярные архитектуры СНС
LeNet
LeNet была представлена Яном Лекуном для распознавания цифр (рис. 14). Она включает 5 сверточных слоев и один полносвязный слой (как MLP). [8, 19]

Рисунок 14 - LeNet, представленная Яном Лекуном
AlexNet
AlexNet содержит 5 сверточных слоев, а также 2 полносвязных слоя для изучения признаков (рис. 15). Она имеет мак-пулинг после первого, второго и пятого сверточных слоев. Всего у неё 650 тыс. нейронов, 60 млн параметров и 630 млн соединений. AlexNet была первой, кто продемонстрировал эффективность глубокого обучения в задачах компьютерного зрения. [2, 7]
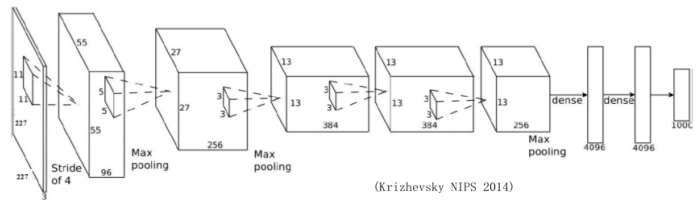
Рисунок 15 - AlexNet, представленная Крижевским, 2014 г.
Вывод
В этой статье мы обсуждаем важные вопросы, связанные со сверточной нейронной сетью (СНС), и объясняем влияние каждого параметра на производительность сети. Самый важный слой в СНС - это сверточный слой, который занимает большую часть времени в сети. Производительность сети также зависит от количества слоёв в сети. Но с другой стороны, по мере увеличения количества слоёв время, необходимое для обучения и тестирования сети увеличивается. Сегодня СНС считается мощным полноценным инструментом машинного обучения для множества приложений, таких как обнаружение лиц и изображений, распознавание видео и распознавание голоса.
Ссылки
- O. Abdel-hamid, L. Deng, and D. Yu, “Exploring Convolutional Neural Network Structures and Optimization Techniques for Speech Recognition, ” no. August, pp. 3366–3370, 2013.
- http://www.deeplearningbook.org/contents/...
- V. Dumoulin and F. Visin, “A guide to convolution arithmetic for deep learning,” pp. 1–28, 2016.
- Y. Guo, Y. Liu, A. Oerlemans, S. Wu, and M. S. Lew, “Author ’ s Accepted Manuscript Deep learning for visual understanding : A review To appear in : Neurocomputing,” 2015.
- https://www.opendatascience.com/blog/....
- I. Kokkinos, E. C. Paris, and G. Group, “Introduction to Deep Learning Convolutional Networks, Dropout, Maxout 1,” pp. 1–70.
- Krizhevsky, A., Sutskever, I. and Hinton, G.E., 2012. Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems (pp. 1097- 1105).
- N. Kwak, “Introduction to Convolutional Neural Networks ( CNNs ),” 2016.
- O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh, S. Ma, Z. Huang, A. Karpathy, C. V Jan, J. Krause, and S. Ma, “ImageNet Large Scale Visual Recognition Challenge.”.
- D. Stutz and L. Beyer, “Understanding Convolutional Neural Networks,” 2014.
- C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, and A. Rabinovich, “Going Deeper with Convolutions,” 2014.
- K. Teilo, “ An Introduction to Convolutional Neural Networks,” no. NOVEMBER 2015, pp. 0–11, 2016.
- R. E. Turner, “Lecture 14 : Convolutional neural networks for computer vision,” 2014.
- J. Wu, “Introduction to Convolutional Neural Networks,” pp. 1–28, 2016.
- https://ujjwalkarn.me/2016/08/11/...
- http://www.slideshare.net/hanneshapke/....
- Wei Xiong , Bo Du, Lefei Zhang, Ruimin Hu, Dacheng Tao "Regularizing Deep Convolutional Neural Networks with a Structured Decorrelation Constraint ” IEEE 16th International Conference on Data Mining (ICDM) , pp. 3366–3370, 2016.
- Taigman, Y., Yang, M., Ranzato, M.A. and Wolf, L., 2014. Deepface: Closing the gap to human-level performance in face verification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 1701-1708).
- LeCun, Y., Bottou, L., Bengio, Y. and Haffner, P., 1998. Gradientbased learning applied to document recognition. Proceedings of the
IEEE, 86(11), pp.2278-2324.