Использование метода конечных элементов (МКЭ) для образования в области нанотехнологий. Прямоугольный кантилевер как датчик массы
Авторы: H. A. Baquero
Перевод: Р. Е. Комаричев
Источник (англ.): Journal of Physics: Conference Series, Volume 582, Number 1. DOI: 10.1088/1742-6596/582/1/012042.
Аннотация
H. A. Baquero — Использование метода конечных элементов (МКЭ) для образования в области нанотехнологий. Прямоугольный кантилевер как датчик массы — Перевод Р. Е. Комаричев. Метод конечных элементов уже достаточно давно является одним из основных в практике расчета зданий и сооружений. Бурное развитие вычислительной техники за несколько последних десятилетий существенно расширило возможности применения этого метода и дало базу для составления новых методик расчета. В данной статье авторы предлагают подборку и краткую характеристику наиболее значимых и интересных зарубежных изданий, посвященных методу конечных элементов (МКЭ), вышедших в свет в начале этого столетия.
Введение
Метод конечных элементов (МКЭ) — это численный метод, предназначенный для решения математических, физических и инженерных задач (структурный анализ, теплопередача, жидкости, массоперенос, электромагнетизм и т.&bnsp;д.). В современно мире МКЭ применяется в таких областях как биомеханика, аэронавтика, геология, электроника, микротехнологии и др. По сути, МКЭ — это метод, позволяющий достичь численной аппроксимации решений дифференциальных уравнений и решений в частных производных [1]. Известно, что, за исключением особых случаев, аналитическое решение этих уравнений невозможно, и единственная оставшаяся возможность - это получить оценочные ответы. МКЭ может быть использован как обучающий инструмент в микро- и нанотехнологиях. В основном он позволяет проверить пригодность кантилеверов как датчиков массы [2][3]. Эти микромеханические датчики могут работать как в статическом, так и в динамическом режиме. В статическом режиме изгиб кантилевера происходит из-за изменения поверхностных напряжений. В динамическом режиме сдвиг резонансной частоты происходит из-за изменений массы и/или жесткости пружины кантилевера. В последнее десятилетие исследователи доказали его чувствительность к распознаванию несовпадений ДНК в статическом режиме [4][5]. В динамическом режиме кантилеверы использовались во многих прикладных областях, например датчики для определения массы отдельной вирусной частицы [6][7][8]. МКЭ использовался в качестве активного инструмента виртуального обучения, который позволял студентам изучать концепции и техники работы с кантилеверами, устраняя необходимость проведения тестов на реальных устройствах.
Теория
Резонансная частота кантилевера, колеблющегося в режиме изгиба в вакууме, определяется как [7]
 |
(1) |
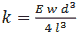 |
(2) |
Напротив, изменения массы можно точно определить, отслеживая резонансную частоту кантилевера во время адсорбции или десорбции массы. Свойства упругости кантилевера остаются неизменными в процессе адсорбции/десорбции молекул, а эффекты демпфирования незначительны. Этот режим работы называется динамическим. Новую резонансную частоту можно записать как
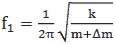 |
(3) |
Изменение массы прямоугольного кантилевера рассчитывается по формуле
 |
(4) |
Частоту 𝑓1 можно записать через 𝑓0 следующим образом:
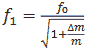 |
(5) |
Ряд Тейлора первого порядка с учетом 𝑓1=𝑓0+𝛥𝑓 приводит к:
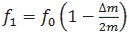 |
(6) |
 |
(7) |
Метод конечных элементов для измерения изменения массы
Была создана CAD-модель кремниевого микрокантилевера (модуль Юнга: 𝐸=131 ГПа, плотность: 𝜌=2330 кг/м3) со следующими размерами: длина 𝑙=600 мкм, ширина: 𝑤=50 мкм и высота: 𝑑=18 мкм (см. рис. 1).

Рисунок 1 — CAD-модель кремниевого микрокантилевера с 𝑙=600 мкм, 𝑤=50 мкм и 𝑑=18 мкм
С помощью МКЭ была получена резонансная частота 𝑓0 первого режима поперечной вибрации микрокантилевера, зажатого на одном конце, как показано на рисунке 2. Поскольку резонансная частота микрокантилевера 𝑓0=60794,47 Гц и его масса m=1,258 мкг, то чувствительность кантилевера к изменению массы 𝜎=0,041 нг/Гц. Создан ряд CAD-моделей; каждая модель имеет свое собственное значение 𝛥m (см. рис. 3). Затем для каждого случая с помощью МКЭ было получено новое значение резонансной частоты 𝑓1, а значения 𝛥m* были взяты из (4), и, наконец, была оценена ошибка. Результаты представлены в таблице 1.

Рисунок 2 — Резонансная частота кремниевого микрокантилевера, вычисленная с помощью МКЭ
Для этой работы использовалось бесплатное программное обеспечение; это означает, что некоторые ограничения проявились в основном на этапе построения сетки, например, ограничение количества узлов и элементов. Однако данные, приведенные в таблице 1, показывают удовлетворительные результаты. Используя платные пакеты МКЭ (ANSYS, COMSOL и т. д.), можно проанализировать и спроектировать микродатчики с улучшенными характеристиками и большей геометрической сложностью.
Рисунок 3 — CAD-модель микрокантилевера с добавленной массой 𝛥m
Таблица 1. Результаты, полученные с помощью МКЭ (значения 𝛥m* получены с помощью МКЭ и (4))
| 𝛥m [нг] | 𝑓0 [Гц] | 𝑓1 [Гц] | 𝛥m* [нг] | (𝛥m*-𝛥m)/𝛥m * 100 [%] |
|---|---|---|---|---|
| 2,097 | 60794,47 | 60589,14 | 2,055 | 2,03 |
| 4,194 | 60794,47 | 60388,93 | 4,079 | 2,73 |
| 6,291 | 60794,47 | 60185,49 | 6,013 | 2,13 |
| 8,388 | 60794,47 | 59985,66 | 7,493 | 2,02 |
| 10,485 | 60794,47 | 59789,41 | 10,262 | 2,12 |
Заключение
Результаты показывают высокое совпадение теоретической модели и виртуального решения проблемы. Сравнение значений массы 𝛥m между CAD-моделью и МКЭ-моделированием с использованием выражения (4) показывает ошибку около 2%. Использование МКЭ при разработке и применении датчиков МЭМС имеет большой потенциал для будущего развития новых стратегий обучения новым технологиям. 3D-моделирование в САПР. Для создания 3D CAD-моделей использовалось бесплатное программное обеспечение FreeCAD 0.13 и FEM LISA 8.0.0. Автор благодарит за частичную финансовую поддержку инженерный факультет в Universidad Distrital через Proyecto Curricular de Ingeniería Electrónica.
Список литературы
- Aya B H, Cano M R and Zhevandrov B P 2011 Ingeniería e investigación, 31 1 7-15.
- Gimzewski J K, Gerber Ch, Meyer E and Schlittler R R 1994 Chem. Phys. Lett.217 589.
- Thundat T, Warmack R J, Chen G Y and Allison D P 1994 Appl. Phys. Lett. 64 2894.
- Fritz J, Baller M K, Lang H P, Rothuizen H, Vettiger P, Meyer E, Güntherodt J G, Gerber Ch and Gimzewski J K 2000 Science288 316.
- Hansen K M, Hai-Feng Ji, Wu G, Datar R, Cote R, Majumdar A and Thundat T 2001 Anal. Chem.73 1567-1571.
- Gupta A, Akin D and Bashir R 2004 Appl. Phys. Lett. 84 1976.
- Chen G Y, Warmack R J, Thundat T, Allison D P and Huang A 1994 Rev. Sci. Instrum. 65 2532.
- Subhashini S and Vimala Juliet A 2013 Computer Networks & Communications (NetCom). Lecture Notes in Electrical Engineering131 75-80.