Классификатор Байеса для переменного количества признаков

Авторы:Г.И. Турканов,Е.В. Щепин
Источник: ЖУРНАЛ "Труды Московского физико-технического института",г. Москва, 2016 год [Ссылка]

Аннотация: Рассматривается подход ранжирования при помощи наивного байесовского классификатора для переменного количества признаков с применением теории фракталов, которая позволяет получить дополнительную информацию в классификаторхарактеристику самоподобия. Для этого будет модифицирован наивный Байесовский классификатор и определен показатель Херста данных, который связан с традиционной фрактальной размерностью.

Ключевые слова: Байесовский классификатор, машинное обучение, ранжирование, показатель Херста, фрактальная размерность, предсказание, вычислительный эксперимент

Введение

Так называемый наивный классификатор Байеса основан на предположении независимости рассматриваемых признаков [1]. А именно, оценка вероятности события по данной совокупности признаков, согласно Байесу, основана на произведении условных вероятностей этого события относительно рассматриваемых признаков.

И несмотря на то, что при практическом применении признаки, как правило, зависимы и байесовские оценки вероятностей могут сильно отличаться от реально наблюдаемых, этот простейший классификатор редко удается существенно превзойти [2].

Для практического применения байесовской оценки первоочередное значение имеет не ее точность, а ее ковариантность наблюдаемой вероятности, выражающаяся в том, что эта оценка тем больше, чем больше наблюдаемая вероятность события [3].

Целью исследований было увеличить точность классификатора при условии переменного количества признаков.

Байесовский классификатор

Существенным условием выполнения свойства ковариантности байесовской оценки является постоянство количества признаков, на основе которых она определяется.

Вероятностная модель для классификатора – это условная модель p(C|x1, x2, ..., xn) над независимой переменной класса C и признаками x1, x2, ..., xn по теореме Байеса [4]:

В свою очередь знаменатель представляет собой масштабный множитель, зависящий только от признаков x1, x2, ..., xn, числитель же эквивалентен совместной вероятности модели:

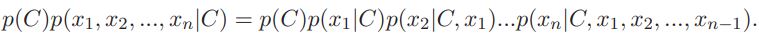
Далее, в наивном байесовском классификаторе используется предположение о независимости признаков x1, x2, ..., xn, то есть

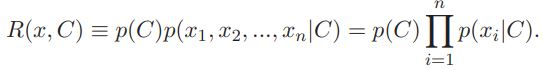
В случае с переменным количеством признаков использование такого классификатора в явном виде приводит к потере его ковариантности, то есть объект с большим количеством признаков получит заведомо заниженную оценку.

Самое простое, что можно сделать в случае переменного количества признаков – это перейти от произведения к среднему геометрическому условных вероятностей. В случае постоянного количества признаков переход от произведения к среднему геометрическому никак не отражается на ковариантности классификатора, а в случае переменного количества, очевидно, ее повышает:

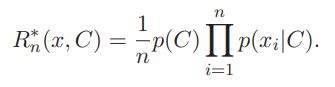
Для дальнейшего повышения ковариантности классификатора в случае переменного количества признаков предложено проанализировать характер зависимости байесовского произведения от количества множителей.

Если общее количество признаков велико (тысячи), тогда как для классификации каждого события применяется лишь небольшая их часть (десятки), то логично ожидать, что логарифм байесовского произведения асимптотически линейно растет с ростом количества сомножителей.

А именно, пусть B(k, n) обозначает среднее значение логарифма байесовского произведения для k наблюдаемых событий с n признаками:

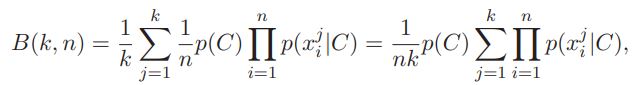
тогда на практике для зависимых признаков нередко можно наблюдать, что разность B(k, n) – nB(k, 1) растет пропорционально некоторой (обычно нецелой) степени количества признаков:

Показатель H этой степени называется показателем Херста. Далее будет показана модификация байесовского классификатора на основе следующего члена асимптотического разложения логарифма байесовского произведения.

Показатель Херста

Известно, что показатель Херста представляет собой меру персистентности — склонности процесса к трендам (в отличие от обычного броуновского движения). Значение H > 1/2 означает, что направленная в определенную сторону динамика процесса в прошлом, вероятнее всего, повлечет продолжение движения в том же направлении. Если H < 1/2 , то прогнозируется, что процесс изменит направленность. H = 1/2 означает неопределенность — броуновское движение [5].

Рассмотрим систему наблюдений (x^n, y)k, где x^n – вектор признаков длины n ∈ {n₁, n₂, ..., n_n }, y – класс из {0, 1}, k – количество наблюдений. Предположим, что значения xn так же принимают значения из {0, 1}. Сперва перейдем к системе (x_j , ctr_j)j=1..F , где F – общее количество признаков, а ctr_j :

где k – количество наблюдений, в которых встречается признак xj , yi – соответствующие этим наблюдениям классы. Далее вычисляется среднее байесовских оценок для различного числа признаков n:

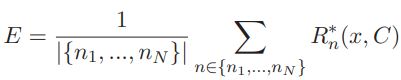
Затем рассчитывается стандартное отклонение:

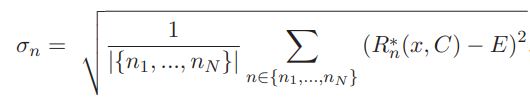
И окончательно в предположении (1) –

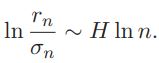
Откуда угол наклона прямой, построенной как аппроксимация последовательности rn/σn :

где

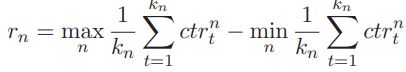
Угол наклона H прямой:

– искомый показатель Херста

Дополнительная информация, которую несет показатель H как коэффициент самоподобия, далее была применена к байесовскому классификатору:

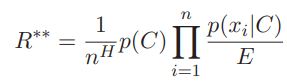
Экспериментальные результаты

В качестве экспериментальной базы использованы данные поисковой системы Yandex. Обучающая выборка была собрана за период с 27.10.2015 по 16.11.2015 и состоит из 24 099 318 пар фраза–баннер с общим числом 440 205 425 показов и 6 685 997 кликов.

Тестовый набор данных был собран с 17.11.2015 по 23.11.2015 и включает в себя 1 139 066 пар фраза–баннер с общим числом 7 182 355 показов и 40 877 кликов.

Метрикой качества выступает количество потерянных кликов по рекламным баннерам в зависимости от порога фильтруемых показов. На графике изображена разница между потерянными кликами, зеленый – наивный байесовский классификатор, синий – модифицированный. Отрицательные значения соответствуют меньшему значению потерянных кликов при одинаковом значении фильтруемых показов.

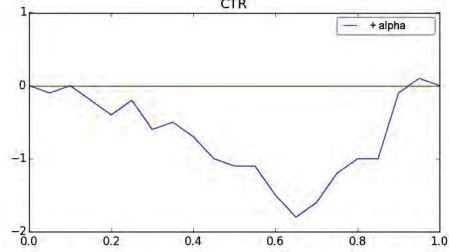
Рисунок 1 –Разница в фильтрованных кликах по наивному байесовскому классификатору и модифицированному

В качестве альтернативной метрики была использована ROC-кривая. Для наивного байесовского классификатора значение площади под кривой составило 0.721377, для модифицированного метода – 0.760481. В качестве бинарной классификации выступало наличие или отсутствие клика в паре фраза–баннер.

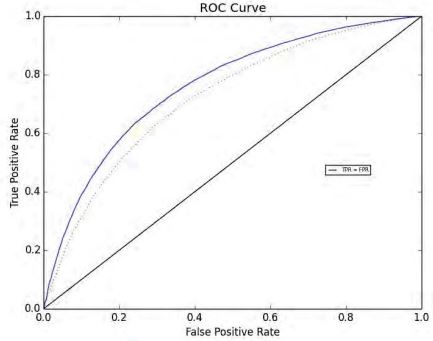
Рисунок 2 –ROC-кривые двух классификаторов, синий – модифицированный метод

Интерпретация результатов

Экспериментальные результаты подтвердили лежащие в основе исследования предположения о положительном вкладе дополнительной информации в предсказание в виде фрактальной размерности.

Показатель H составил 0, 68, что говорит о периодичной зависимости в данных. Улучшение в предсказании наблюдается на всем промежутке фильтруемых показов рекламных баннеров, относительное улучшение до 6% кликов.

Для подтверждения предположения о связи между показателем H и зависимостью используемых признаков был произведен еще один эксперимент. В исходные данные было добавлено искажение в виде дублирования 20% признаков, что привело к увеличению показателя H до 0, 81 и ухудшения классификатора по сравнению с более независимыми признаками.

Литература

Russell S., Norvig P. Artificial Intelligence: A Modern Approach (2nd ed.). New York: Prentice Hall, 2003.
Graepel T., Candela J., Borchert T., Herbrich R. Web-Scale Bayesian click-through rate prediction for sponsored search advertising in Microsoft’s Bing search engine // Proceedings of 27th International Conference on Machine Learning. 2010. P. 13–20.
Turkanov G. Modified Naive Bayes with Hurst exponent as quantitative measure of data mutual dependence // Proceedings of Yandex School of Data Analysis Conference. Machine Learning: Prospects and Applications. 2015.
Bayes T. An essay, towards solving a problem in the doctrine of chances // Philos Trans R Soc Lond. 1763. V. 53. P. 370–418.
Feder J. Fractals. New York: Plenum Press, 1988.