Программная реализация методов классификации
Авторы:И.Н. Егорова,С.В. Егоров Источник: Восточно-Европейский журнал передовых технологий,2020 год [Ссылка]
Аннотация: Проведено исследование метода деревьев решений, реализованного в виде алгоритма ID3, и метода k - ближайших соседей, реализованного в виде алгоритмов KNN и Fuzzy KNN. Осуществлена программная реализация алгоритмов классификации
Ключевые слова:алгоритмы классификации, распознавание, образ, программная реализация
Введение
Методы классификации используются в задачах распознавания образов, которые представляют собой, по существу, дискретные аналоги задач поиска оптимальных решений. К ним относится широкий класс задач, в которых по некоторой, обычно весьма разнородной и, может быть неполной или косвенной информации требуется установить, обладают ли изучаемые объекты фиксированным конечным набором свойств, позволяющим отнести их к определенному классу, - задачи распознавания и классификации. Аналогичного рода информация о конечном множестве достаточно однотипных процессов служит для выяснения в какой области из конечного числа областей будут находиться эти процессы через определенный период времени - задачи прогнозирования.
Автоматизация процедур распознавания становится элементом автоматизации процессов принятия решений и представляется задачей актуальной.
Анализ проблемы
Классификацией является задача разбиения множества объектов или наблюдений на априорно заданные группы, называемые классами, внутри каждой из которых они предполагаются похожими друг на друга, имеющими примерно одинаковые свойства и признаки. При этом решение формируется на основе анализа значений атрибутов.
В настоящее время классификация применяется в маркетинге при оценке кредитоспособности заемщиков, определении лояльности клиентов, распознавании образов, медицинской диагностике и многих других приложениях [1]. Если аналитику известны свойства объектов каждого класса, то когда новое наблюдение относится к определенному классу, данные свойства автоматически распространяются и на него.
Существует большое множество алгоритмов, реализующих методы классификации. Представляет интерес исследование алгоритмов классификации для выявления среди них наиболее эффективных с целью их последующей программной реализации.
В дальнейшем необходимо осуществить оптимизацию вычислительной сложности алгоритмов для повышения скорости обработки больших объемов данных в масштабах реального времени.
Постановка задачи исследования
Для классификации в настоящее время используется множество различных методов: нейронные сети, деревья решений, машины опорных векторов, метод k - ближайших соседей, алгоритмы покрытия и др., при построении которых применяется обучение с учителем, когда выходная переменная задана для каждого наблюдения. Формально классификация производится на основе разбиения пространства признаков на области, в пределах каждой из которых многомерные векторы рассматриваются как идентичные.
Иными словами, если объект попал в область пространства, ассоциированную с определенным классом, он к нему и относится [2].
Проведенное исследование показывает, что наиболее эффективными являются методы деревьев решений и k - ближайших соседей.
В основе метода деревьев решений лежит принцип обучения на метках классов учебных выборок. Дерево решений является графоподобной древовидной структурой, где каждый внутренний узел обозначает тестовое условие атрибута, каждая ветвь показывает результаты выполнения тестового условия, и каждая листовая вершина содержит метку класса. Пример дерева решений представлен на рис. 1.
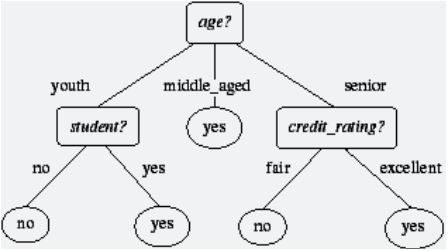
Рисунок 1 – Дерево решений
Метод деревьев решений реализован в виде алгоритма ID3.
Метод k - ближайших соседей позволяет успешно решать задачу обучения с учителем и ориентирован на работу с базами данных большого объема.
Метод k - ближайших соседей реализован в виде алгоритма KNN, принцип работы которого заключается в отнесении элемента выборки к такому классу, к которому относится наибольшее количество k - соседей данного элемента из обучающей выборки.
Алгоритм Fuzzy KNN является модификацией алгоритма KNN и позволяет более точно классифицировать объекты за счет использования функции, которая определяет вероятность вхождения i-го элемента выборки в j-й класс k—ближайшего соседа. Такая функция будет иметь вид:
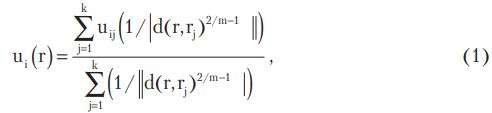
где ui(r) - членство r в классе i; uij - членство в i - м классе j - го элемента обучающей выборки; d (r,rj)- расстояние между элементом неклассифицированной выборки r и j - м элементом обучающей выборки rj.
Исходными данными для работы алгоритмов классификации могут служить различного рода изображения (2D, 3D), цифровая и символьная информация.
Целью работы является программная реализация наиболее эффективных алгоритмов классификации, выбранных на основе проведенного исследования, а также программная реализация и использование алгоритмов кластеризации для обучения классификатора объектов.
Программная реализация
Программное обеспечение реализовано в виде интерфейса пользователя, содержащего классы, созданные для работы алгоритмов классификации, и on - line формы - для отображения результатов выполнения алгоритмов.
Интерфейс пользователя, разработанный в среде Microsoft Visual Studio 2005 [3,4], представлен в виде Windows - приложения (рис. 2). В верхней части главного окна приложения расположено меню, предназначенное для выбора файлов, алгоритмов для их обработки, а также для просмотра справки по программе. В нижней части расположены панели, содержащие информацию о загруженном файле. Правая часть окна содержит элементы управления приложением и алгоритмами.
В зависимости от выбранного типа алгоритма, активизируются различные группы элементов в правой части окна.
Таким образом вводятся необходимые исходные данные для выбранного алгоритма. Алгоритмы кластеризации могут быть использованы как для решения самостоятельной задачи разбиения множества точек на непересекающиеся классы, так и для обучения классификатора объектов и его последующего использования при решении задачи классификации.
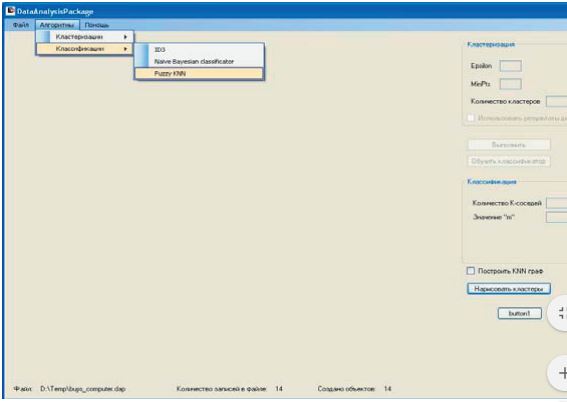
Рисунок 2 – Интерфейс пользователя
Центральная часть главного окна приложения предназначена для отображения результатов работы алгоритмов.
В работе предусмотрена возможность построения KNN - покрытия, т.е. ассиметричного графа, отображающего результаты выполнения алгоритма классификации Fuzzy KNN. Построение осуществляется по принципу соединения ребром текущей точки классифицированной выборки с ближайшей к ней точкой. KNN - покрытие отображается на on - line форме, созданной с помощью библиотек Microsoft DirectX SDK.
Результаты построения KNN—покрытия представлены на рис. 3.

Рисунок 3 – KNN—покрытие
Проведенный в работе анализ алгоритмов показал, что алгоритм ID3, KNN и Fuzzy KNN наиболее эффективны для решения задач распознавания образов с большим объемом исходных данных. KNN—покрытие, построенное для алгоритмов KNN и Fuzzy KNN, позволяет сделать более наглядным конечный результат классификации и упростить процедуру распознавания.
Выводы
В работе проведено исследование существующих методов классификации, а именно: метода деревьев решений и метода k—ближайших соседей. Осуществлен выбор наиболее эффективных алгоритмов, реализующих эти методы. Такими алгоритмами являются ID3, KNN и Fuzzy KNN. Разработано программное обеспечение, которое позволяет использовать эти алгоритмы для решения задач распознавания образов.
Для решения задачи «обучение с учителем» в работе предусмотрена возможность предварительного обучения классификатора объектов посредством решения задачи кластеризации.
В работе осуществлена оптимизация вычислительной сложности алгоритмов для повышения скорости обработки информации в реальном масштабе времени для задач, содержащих большие объемы исходных данных.
В процессе разработки приложения применялись различные виды тестирования, позволяющие сделать вывод о пригодности программы для эксплуатации в реальных условиях, ее надежности, отказоустойчивости и удобстве в применении.
Литература
- Дуда Р., Харт П. Распознавание образов и анализ сцен.- М.: «Мир», 1976.- 507 с.
- Sameer A. A Simple Algorithm for Nearest Neighbor Search in High Dimensions // Department of computer science. - New York, 1998. - 36 p.
- Троелсен Э. С# и платформа .NET. Библиотека программиста. - СПб.: Питер, 2004. - 796 с.
- Liberty J. Programming C#. 2nd ed., - O’Reilly, 2002. - 648 p.