Аннотация
L. He & J.F. Xu Усовершенствованный алгоритм динамической метки программного обеспечения ЦВЗ на основе R-дерева. Чтобы решить проблему низкой скорости внедрения данных и плохой защищенности от несанкционированного доступа алгоритма метки ПО, на основе R-дерева, мы предлагаем метод распределённой метки ПО, основанный на правиле переноса переменной m-n для предварительной обработки водяных знаков программного обеспечения. При внедрении водяных знаков алгоритм объединил исходную последовательность записей в узлах R-дерева с исходным водяным знаком, чтобы сформировать новый встроенный водяной знак. Теоретический анализ и экспериментальные результаты показывают, что схема может эффективно увеличить скорость внедрения данных водяных знаков, а также повысить надежность и защищенность от несанкционированного доступа.
1 Введение
Пометка ПО - важная отрасль технологии ЦВЗ[1,2], которая эффективно защищает интересы потребителей и разработчиков программного обеспечения путем внедрения некоторой информации, идентифицирующей автора, издателя, владельца и пользователя программного обеспечения.
Технология динамической метки ПО, основанная на структурах данных, использует топологические свойства или избыточную информацию узлов конкретных структур данных (например, списков, графиков, деревьев) для скрытия водяного знака[3-5]. В литературе[6] был предложен динамический алгоритм метки ПО, основанный на правиле переноса переменной m-n для предварительной обработки водяных знаков в сочетании с совершенной хэш-функцией и используемым графом перестановок для кодирования. Этот метод может эффективно контролировать гранулярность разделения водяных знаков, и его скорость внедрения данных выше, но его способность противостоять атаке разделенных классов слаба[6]. В литературе[7] Ибрагим Камель (англ. Ibrahim Kamel) и Кутайба Алблуви (англ. Qutaiba Albluwi) предложили технологию динамической метки ПО, с применением R-дерева, в которой водяной знак был встроен в избыточность в порядке записей внутри узлов R-дерева и кодировался системой факторных чисел с переменным основанием (VF-NS). Метод опирается на структуру данных R-дерева, построенную на программе, и обладает высокой надежностью, но его скорость внедрения данных ниже, а защищенность от несанкционированного доступа слаба[7].
Основываясь на приведенном выше анализе, в данной работе предлагается новая динамическая схема пометки ПО, основанная на структуре R-дерева. Схема основана на правиле переноса переменной m-n для предварительной обработки водяных знаков программного обеспечения, а затем использует факторальную систему счисления с переменным основанием для кодирования водяных знаков, что может улучшить скорость внедрения данных. В то же время программа объединит исходную последовательность записей в узлах R-дерева с исходными водяными знаками, чтобы сформировать новый встроенный водяной знак для улучшения защиты от несанкционированного доступа.
2 Теоретический обзор
2.1 Распределение ЦВЗ на основе правила переноса переменной m-n
Распределение метки в программном обеспечении[8] - это процесс предварительной обработки. В настоящей работе используется правило переноса переменной m-n[8] для разложения ЦВЗ на множество суб-ЦВЗ.
Теорема 1: Допустим, Pmn - перестановка m элементов из ряда {1, 2, …, n}, тогда любое целое число 0 – Pmn – 1 может быть представлено в виде:
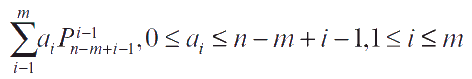
Последовательность (am, am-1,..., a1) называется числом переноса переменной m-n, представляющая собой бит i, который соответствует каждому 0 ≤ ai ≤ n – m + i – 1 и n – m + i в одной из систем счисления.
Когда мы преобразуем W в коэффициент переноса переменной m-n (am, am-1,..., a1), то (am, am-1,..., a1) будет сохранен как общий водяной знак (Wm, Wm-1,..., W1).
Например, допустим: m = 3, а n = 6, тогда P36 = 120. Если ЦВЗ W = 106, то W ∈ [0, P36–1]
То: (106)10 = 2*P03+1*P14+5*P25.
В результате W = 106 будет сохранён как распределённый ЦВЗ (W3, W2, W1) = (5, 1, 2).
2.2 Нуль–кодирование
Допустим, что (Wm, Wm–1, ..., Wi, ..., W1) – встроенный ЦВЗ, а последовательность (E1, E2, ..., Eq) – перестановка записей внутри узла, и сохранить Wi(m ≥i ≥1) в уполядоченные записи следующим образом:
Пусть i % q = j, тогда Ej кодируется как E0, а остальные индексы последовательности кодируются как последовательность натуральных чисел {1, 2, ..., n–1}.
Такая форма кодировки называется "Нуль–кодирование".
2.3 Факториальная система счисления с переменным основаниием (VF-NS)
Теорема 2 [7]: Предположим, что n∈0~m!–1, тогда любое целое число может быть представлено в виде:
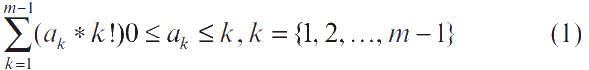
Если натуральное число n = Σlk=1(ak*k!), 0 ≤ ak ≤ k, k = {1, 2, ..., l}, al ≠ 0, тогда (al, al-1, ..., a1) называется факториальным числом переменного основания, которое является кодировкой VF-NS.
Например: целое число 769 в 10-й системе счисления может быть представлено как:
(769)10 = 1*1! + 0*2! + 0*3! + 2*4! + 0*5! + 1*6! = (102001)VF-NS.
Чтобы реализовать уникальность водяного знака, мы создаем взаимно однозначное отображение между всеми перестановками элементов узла R-дерева и всеми возможными значениями водяного знака W. VF-NS предоставляет нам подходящее решение для этого сопоставления один-к-одному.
2.4 Работа с R-деревом
R-деревья - это расширения B+-деревьев для многомерных объектов [9]. R-деревья используют технологию определения границ объектов, геометрический объект представлен минимальным ограничивающим его прямоугольником (МОП), а узлы разделены на два типа:
- Не-листовые узлы содержат записи вида (ptr, R), где ptr - указатель на дочерний узел в R-дереве, а R - это МОП, который охватывает все прямоугольники в дочерних узлах. Как показано на рис. 1 A, B и C - не-листовые узлы, где A охватывает МОП своих дочерных узлов D, E, F.
- Листовые узлы - содержат записи формы (obj-id, R), где obj-id - указатель на описание объекта, а R - МОП объекта.
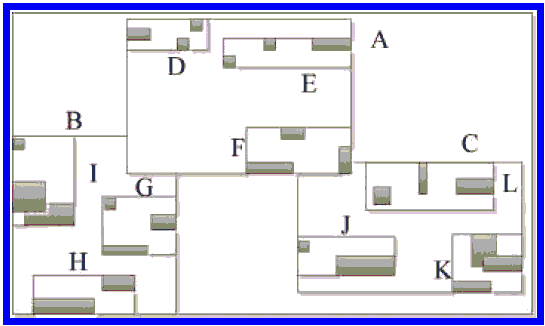
Рисунок 1 - Пример МОП R-дерева
Как показан на рис. 1 - D, E, F, G, H, I, J, K и L - листовые узлы.
Из-за того что структура листовых узлов схожа со структурой не-листовых узлов, то предложенная схема метки не различает листовые и не-листовые узлы.
В сравнении с B-деревом, наибольшим преимуществом R-дерева является его независимость от порядка записей в узлах. Алгоритм метки ПО на основе R-дерева использует это преимущество, и скрывает метку изменяя порядок записей в дереве.
3 Усовершенствованный алгоритм метки ПО на основе R-дерева
3.1 Обзор алгоритма
В литературе [7], алгоритм метки ПО на основе R-дерева имеет высокую надёжность, но скорость встраивания данных низка, а защита от несанкционированного доступа слаба.
Для решения этой проблемы, мы планируем улучшить исходный алгоритм, представив следующий алгоритм.
Во-первых, мы используем правило перестановки переменных m-n чтобы разделить W на W' = (Wm, Wm-1, ..., W1), после чего мы комбинируем W' с последовательностью ER исходных записей, чтобы сформировать новый распределённый ЦВЗ WR = (W'm, W'm-1, ..., W'1), а после, мы используем VF-NS, чтобы закодировать WR в форму Wj = (W'm, W'm-1, ..., W'1), затем встраисаем ЦВЗ Wf в узлы по очереди. Рис. 2 изображает всю структуру алгоритма.
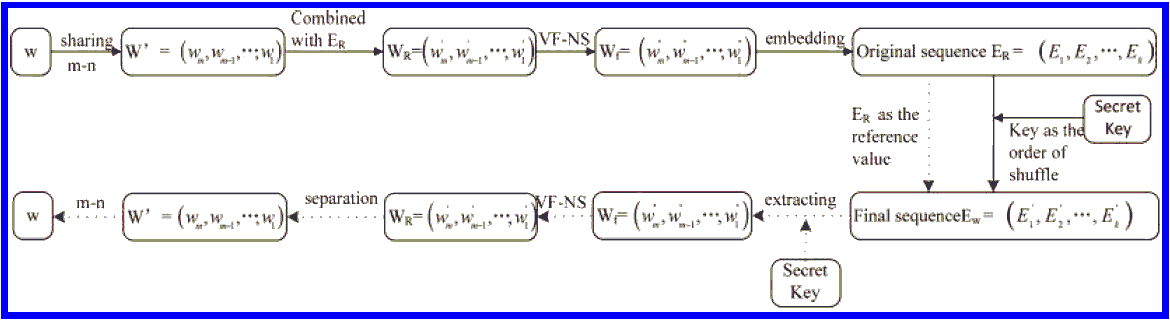
Рисунок 2 - Усовершенствованный процесс пометки и извлечения метки на основе R-дерева
3.2 Встраивание ЦВЗ на основе R-дерева
Алгоритм встраивания ЦВЗ на основе R-дерева разделён на следующие шесть этапов:
- Нумерация узла: R-дерево растёт снизу вверх[9], и мы изпользуем эту структуру чтобы спрятать ЦВЗ в одном, нескольких, или во всех узлах. Мы используем метод обхода в ширину, а каждый узел нумеруется Ni(i=1, 2, ..., N).
- Распределение ЦВЗ: мы преобразуем W в m-n номер переноса переменной W' = (Wm, Wm-1, ..., W1) и владелец ПО должен записать количество суб-ЦВЗ m.
- Встраивание ЦВЗ: в соответствии с 1-м этапом мы встраиваем Wm в NN, Wm-1 в NN-1, ... ...; если последний слой узлов использован, мы можем встроить ЦВЗ Wi(m ≤ i ≤ 1) в предыдущем слое узлов, пока ЦВЗ не будет встроен полностью. В то же время продолжаем выполнять этапы 4-6.
- Объединение входной последовательности с распределённым ЦВЗ: в соответствии с нуль–кодированием и 2-м этапом, мы объединяем распределённые ЦВЗ Wi(1 ≤ i ≤ m) с последовательностью первых k записей ER(k ≤ R ≤ K) (k - минимальное количество записей в узеле, а K - максимальное, при k = K / 2) в узлах R-дерева Ni = (i = 1, 2, ..., N), так Ei%k закодировано как E0, другие индексы R закодированы как натуральные числа. Таким образом, номер записи - (E1, E2, ..., E0, ..., Ek-1). После мы складываем Wi(1 ≤ i ≤ m) и сумму k(k-1)/2 индексов записей, и сохраняем сумму как новые ЦВЗ W'i(1 ≤ i ≤ m).
- VF-NS кодирование: мы используем VF-NS, чтобы закодировать Wi(1 ≤ i ≤ m) в новый ЦВЗ Wi(1 ≤ i ≤ m).
- Перемешивание: В соответствии с секретной инструкцией, которая заранее составлена и известна только владельцу ПО. Секретная инструкция эквивалентна секретному ключу. Здесь используются инструкции такие как "Вращать влево". Таким образом мы перемешиваем записи (E1, E2, ..., E0, ..., Ek-1) в последующих шагах, где каждое значение W'i(1 ≤ i ≤ m) = соответствуем количеству каждого цикла.
Допустим, ЦВЗ имеет значение W'i(1 ≤ i ≤ m) = "311", а ER = (E1, E0, 2, E3) (см. рис. 3).
Первая цифра в W'i - "3", тогда записи (E1, E0, 2, E3) будут передвинуты на три позиции, давая в результате последовательность (E3, E1, 0, E2).
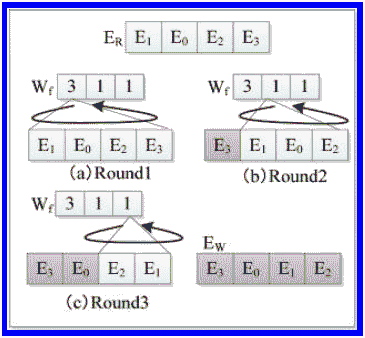
Рисунок 3 - Процесс встраивания ЦВЗ
Первая запись (E3) будет зафиксирована, а записи (E1, E0, E2) будут передвинуты только один раз, потому что следующая цифра - "1", тогда новая последовательность - (E3, E0, E2, E1). Оставшиеся записи (E2) и (E1)) будут передвинуты один раз, потому что третья цифра - "1".
Окончательная последовательность (ЦВЗ) должна быть (E3, E0, E1, E2). Результирующий узел мы обозначим как EW = (E3, E0, E1, E2).
3.3 Процесс извлечения ЦВЗ
Процесс извлечения может быть разделён на следующие этапы:
- Извлечеие ЦВЗ Wf = (W'm, W'm-1, W'1):
в соответствии с "секретным ключом", мы сравниваем ER с EW на совпадение каждой записи в узлах.
Число операций цикличных сдвигов нужно, чтобы выровнять элемент из ER с соответствующим элементом из EW, который составлял ЦВЗ
Wf = (W'm, W'm-1, W'1).
Как показано на рисунке 3, исходная последовательность записей (ER = (E1, E0, E2, E3)), после встраивания превратилась в EW = (E3, E0, E1, E2), таким образом мы можем получить встроенный ЦВЗ W''i = "311". На рисунке 4 изображён процесс извлечения ЦВЗ.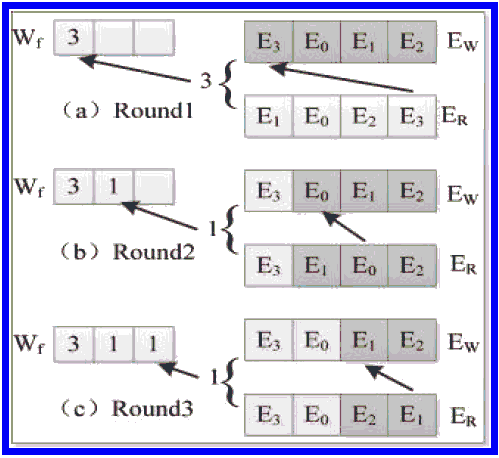
Рисунок 4 - Процесс извлечения ЦВЗ
- Отделение и восстановление ЦВЗ: Отделение ЦВЗ Wf = (W'm, W'm-1, W'1) один за одним, каждое значение W''i(1 ≤ i ≤ m) минус k(k-1)/2; после чего преобразуем Wf в десятичную форму, на основе VF-NS, что даст в результате значение W' = (Wm, Wm-1, ..., W1), и в соответствии с правилом переноса переменных m-n возвращаем W' в форму исходного ЦВЗ W.
4 Анализ производительности
4.1 Устойчивость к атакам
Атаки против ЦВЗ программного обеспечения могут быть разделены на четыре основные категории: субтрактивные, искажающие, аддитивные и атаки сговора[11].
Поскольку водяной знак кодируется в относительном порядке записей внутри узлов R-дерева, субтрактивные атаки не могут быть использованы против предложенного метода водяных знаков. Если злоумышленник устраняет водяные знаки, ему нужно удалить половину записей в узле. В этом случае производительность кода будет значительно снижена или он может работать неправильно.
В искажающих атаках, как только владелец обнаружил атаки, при вставке новых узлов в R-дерево будет работать алгоритм встраивания водяного знака и снова создаст водяной знак. Таким образом, владельцы программного обеспечения все еще могут доказать свое право собственности. При атаках сговором конечным результатом является устранение водяных знаков, что также повлияет на нормальную работу программы. Таким образом, атаки сговора не могут быть вызваны против предложенного алгоритма водяных знаков.
4.2 Защита от несанкционированного доступа
Мы предлагаем объединить исходную последовательность записей внутри узлов R-дерева с исходным водяным знаком, чтобы сформировать новый встроенный водяной знак. Затем, даже без добавления новых узлов, когда водяной знак извлекается, нам все равно нужно отделить встроенный водяной знак. Поэтому, если злоумышленник не знает кодовую последовательность исходных записей, ему трудно отделить водяной знак, и подделка атак станет недействительной.
Как показано в Таблице 1, предлагаемый алгоритм водяных знаков может эффективно противостоять распространенным программным атакам водяных знаков и может эффективно улучшить защиту от несанкционированного доступа.
| Алгоритм | Аддитивная атака | Субтрактивная атака и атака сговором | Искажающая атака | Несанкционированный доступ |
|---|---|---|---|---|
| Оригинальный алгоритм | Слабая | Сильная | Сильная | Слабая |
| Усовершенствованный алгоритм | Сильная | Сильная | Сильная | Сильная |
4.3 Скорость встраивания данных
В литературе[7] водяной знак встроен в первые K/2 записи внутри всех узлов R-дерева, и встроенные водяные знаки в каждом узле одинаковы. Согласно VF-NS, предположим, что у нас есть k элементов, перестановка k элементов = Pkk = k!, исключая начальное состояние k!-1. Для встраивания водяного знака в k позиций максимальное значение водяного знака может быть представлено в виде (k + 1)! - 1.
В данной работе предлагаемая схема хранит водяной знак в нескольких узлах или во всех узлах, и каждое значение водяного знака в каждом узле не является одинаковым. По сравнению с оригинальным алгоритмом, улучшенному алгоритму нужно только выбрать соответствующие m и n, во время встраивания водяного знака в k записей, значение водяного знака будет намного больше, чем (k + 1)! - 1.
4.4 Анализ производительности перегрузки
Существует два основных типа воздействия на работоспособность алгоритма: пространственная перегрузка и временная перегрузка.
В физическом пространстве алгоритм метки ПО на основе R-tree не занимает дополнительного дискового пространства, а скрывает водяной знак, изменяя порядок исходных записей внутри узла. Поэтому встраивание водяного знака не изменит размер R-дерева.
Во временной производительности, как показано на Рис. 5, Время встраивания водяного знака увеличивается квадратично с числом записей в узле. Например, для R-дерева с размером узла 200 стоимость вставки водяного знака близка к 20 мс, что эквивалентно одному доступу к диску. Однако эти затраты возникают только при операции разделения, поэтому накладные расходы приемлемы.
На рис. 6 ось y показывает соотношение между временем вложения и временем разделения узла; ось x показывает количество записей внутри узла R-дерева. Следует отметить, что отношение стоимости вставки водяного знака к стоимости разделения ниже 0,25 для размеров узлов ниже 200, в то время как для размеров узлов 200-400 это соотношение составляет от 0,25 до 0,5. На практике большинство R-деревьев имеют размер узла ниже 400, а операция разбиения является наименее частой операцией, и поэтому увеличение ее времени с разумной долей (0,2–0,5) является приемлемым.
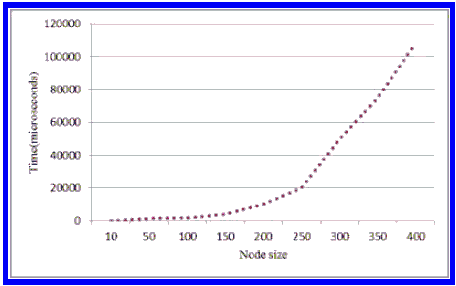
Рисунок 5 - Затраты на встраивание ЦВЗ
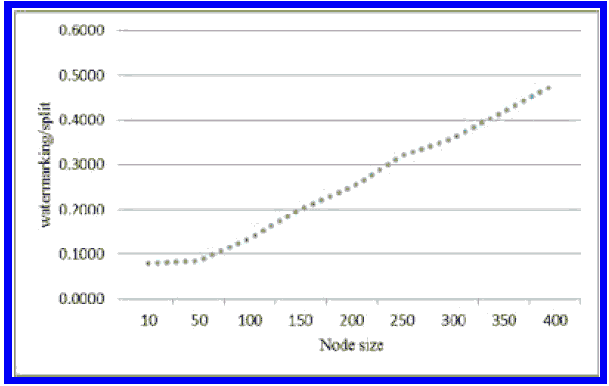
Рисунок 6 - Соотношение между временем на встраивание и на разделение узлов
5 Заключение
Основываясь на анализе и исследовании метки ПО на основе R-дерева, мы используем правило переноса переменных m-n для совместного использования водяного знака с суб-ЦВЗ знаками и объединяем внутреннюю последовательность ввода внутри узлов R-дерева с исходным водяным знаком. После извлечения водяного знака нам нужно отделить встроенный водяной знак, чтобы получить исходный водяной знак. По сравнению с оригинальным алгоритмом, усовершенствованный алгоритм не увеличивает размер объекта и времемя выполнения, а эффективно улучшает скорость встраивания данных и защищенность от несанкционированного доступа. В дальнейшем мы будем учиться сочетать программные функции с водяным знаком, чтобы улучшить незаметность и доступность алгоритма метки ПО.
Ссылки
1. Zhu, W.F. 2007. Concepts and techniques in software watermarking and obfuscation. Auckland: The University of Auckland New Zealand.
2. Liu, M. 2011. The Research of Dynamic Graph Software Watermarking Algorithm Based on Tamperproof Technology. Guangzhou: Jiangxi University of Science and Technology.
3. Zhang, L.H. & Yi, X. 2003. A Survey on Software Watermarking. Journal of Software 14(2): 268–277.
4. Wang, Y.S. & Xu, J.F. 2012. Improved PPCT Hybrid Coding Scheme. Computer Engineering and Applications 48(34): 107–111.
5. Collberg, C. & Thomborson, C. 1999. Software watermarking: Models and dynamic embeddings. Proceedings of the 26th ACM SIGPLAN-SIGACT symposium on Principles of programming languages: 311–324.
6. Li, S.Z. & Wang, X.M. 2012. Dynamic Graph Software Watermarking Algorithm Based on m-n Variable Carrying Rule. Computer Engineering 38(21): 17–21.
7. Kamel, I. & Albluwi, Q. 2009. A robust software watermarking for copyright protection. Computers & Security 28(6): 395–409.
8. Wang, X.M. 2013: The Research of Software Watermarking Sharing and Encoding Algorithm Based on The Tamper-proof Technology. Ganzhou: Jiangxi University of Science and Technology.
9. Guttman, A. 1984: R-trees: a dynamic index structure for spatial searching. In New York, ACM: 47–57.
10. Zhang, M.B. & Lu, F. 2005: The Evolvement and Progress of R-tree Family. Chinese Journal of Computers 28(03): 289–300.
11. Li, L. 2008: A Suvery on Attacks on Software Watermarking. In Qingdao, The 15th at the Chinese academy of electronic information theory academic annual meeting and proceedings of the first national network coding academic conference(I): 525–530.