Аннотация
В.М. Рувiнська, Р.А. Айрапетян, Є.Л. Беркович Метод захисту програмного забезпечення задопомогою вбудованих мереж Петрі. Запропоновано метод захисту програм за допомогою мереж Петрі, який дозволить захистити програму від налагодження. Суть методу полягає у тому, що умовний перехід, який залежить від введеного ключа,виявляється максимально прихованим і недосяжним для зломщика.
V.M. Ruvinskaya, R.A. Airapetyan, E.L. Berkovich. Approach for application protection with built-in Petri nets. A method for software protection with the use of Petri nets, which will allow to protect the program from debugging is offered. The point of the method is that conditional transition, which dependson the input key, appears maximally hidden and unattainable for a hacker.
Проблема защиты программного обеспечения от нелегального использования актуальна. Чаще всего в исходный код защищаемой программы встраивают специальный фрагмент, с помощью которого проверяется, правильно ли пользователь зарегистрировался, и сравниваются встроенный и введенный при регистрации ключ. Этот фрагмент содержит переходы, зависящие от результата сравнения, на различные части программы (условные переходы). Взломщик ищет его в программе и обходит проверку.
Методы защиты программ от взлома делятся на два типа: антидизассемблерные и антиотладочные [1]. Главная задача антидизассемблерных методов заключается в максимальном усложнении статического анализа исходного кода программы. Все методы сводятся к шифрованию (и/или архивации) отдельных секций или всего исходного программного кода, а также к использованию техники самомодифицирующегося кода (Self-Modifying Code - SMC). Кроме усложнения статического анализа исходного кода программы, антидизассемблерные приемы позволяют защитить модуль от внесения в его тело каких-либо изменений.
Однако большинство популярных компиляторов (Visual C, Visual Basic и т.д.) компилируют исходный код программы таким образом, что он практически не поддается никакому анализу, т.е. настолько сложен сам по себе, что обычно не нуждается в дополнительном шифровании. Поэтому для взлома современных программ чаще всего используют их динамический анализ, а именно, применяют различные отладчики [1] и следят за работой программы для определения места проверки ключа.
Существуют различные методы защиты программ от отладки. Наиболее известные из них специальным образом изменяют, например, блокируют работу отладочных средств, таких как отладочные регистры, обработчики исключений и др., чтобы взломщик не смог ими воспользоваться [1].
Однако в ответ на различные создаваемые средства защиты хакеры изобретают соответствующие способы их взлома, поэтому необходимо постоянно разрабатывать новые подходы.
Известен подход для защиты программ от отладки - вместо блокирования отладочных средств осуществляется усложнение фрагмента, включающего сравнение ключей и условные переходы, который определяет, является ли использование запущенной программы легальным или нелегальным, т.е. максимальное усложнение поиска места проверки ключа в программе [2].
Для реализации такого подхода предлагается метод защиты программного обеспечения с помощью встроенных в исходный код программы сетей Петри, выбранных потому, что они удобны для моделирования условных переходов, а также потому, что их можно “наращивать” и тем самым усложнять поиск фрагмента проверки ключа.
Сеть Петри - это двудольный ориентированный граф, состоящий из позиций p, переходов t, а также дуг, связывающих позиции с переходами и наоборот(рис. 1) [3]. Входные и выходные позиции для переходов обычно задают в виде таблиц (матриц), которые определяют входную и выходную функции (отображения из переходов в комплекты позиций). Далее будут использоваться маркированные сети Петри. Маркировка µ - присвоение фишек позициям сети Петри. Фишки используются для выполнения сети Петри, что происходит посредством запусков переходов. Переход называется разрешенным, если каждая из его входных позиций имеет число фишек, по крайней мере равное числу дуг из позиции в переход. Переход запускается удалением фишек из его входных позиций и образованием новых фишек, помещаемых в его выходные позиции. Позиции обычно обозначают кружками, переходы - черточками, функции - дугами, а фишки - точками. Использование сетей Петри с приоритетами означает, что переходам будут назначаться приоритеты, т.е. если могут одновременно выполниться несколько переходов, запустится имеющий более высокий приоритет.
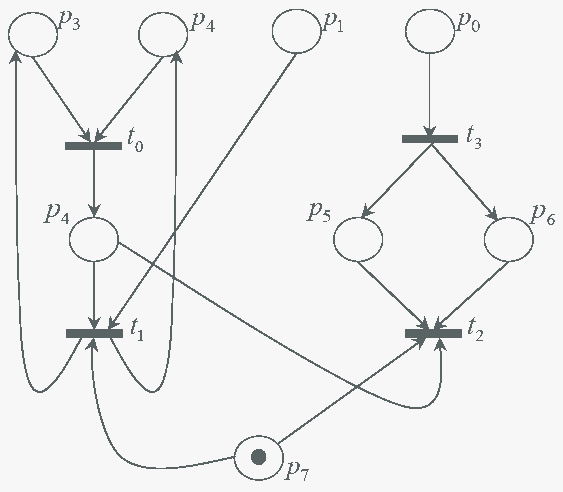
Рисунок 1 - Простая сеть Петри для защиты программ от отладки
Предлагаются способы усложнения встраиваемой сети Петри, а также пути реализации защитного механизма. Суть метода в том, что к защищаемой программе добавляется защитный фрагмент программного кода, реализующий запуск специально разработанной сети Петри. Эта сеть содержит несколько позиций p, которые используются для задания начальной маркировки, - “начальные” позиции, и в них перед запуском сети записывается введенный пользователем ключ (количество таких позиций равно количеству битов в ключе). В сети есть переход t, который срабатывает тогда и только тогда, когда введен правильный ключ, т.е. “решающий” переход.
После ввода ключа защитный фрагмент записывает фишки в те позиции для начальной маркировки, где стоят единицы в соответствующих битах ключа. Затем запускается сеть Петри. Если ключ введен правильно, сработает “решающий” переход, и программа продолжит работу. Если введен неверный ключ, “решающий” переход будет недостижим, будет выведено сообщение, что ключ неверен.
Допустим, необходимо ввести 4-битный ключ, и позициями для начальной маркировки, куда будет записываться ключ, являются p0,…, p3 (см. рисунок 1). Позиция p7 всегда имеет одну фишку. Остальные позиции при начальной маркировке вообще не имеют фишек. “Решающий” переход обозначен t2. Программа считается зарегистрированной, если переход t2 сработает, т.е. будет активным.
Зададим переходу t2 приоритет ниже, чем переходу t1, т.е. если одновременно разрешены оба перехода, то сработает переход t1.
Утверждение. Переход t2 выполнится тогда и только тогда, когда начальная маркировка помечает позиции p0,…, p3 следующим образом: p0=1, p1=0, p2=1, p3=1.
Действительно, при таком значении ключа выполнятся переходы t0 и t3, после этого позиции p4, p5 и p6 будут иметь по одной фишке, сработает “решающий” переход t2. Если хотя бы одна из позиций p0, p2 и p3 не содержит фишек, то не выполнится переход t0 или t3, что не позволит сработать и “решающему” переходу. Поэтому позиции p0, p2 и p3 должны обязательно содержать по одной фишке. Остается открытым вопрос с p1. Если p1=1, то может сработать и переход t1, и переход t2. Чтобы первым сработал t1, ему назначается более высокий приоритет, его выполнение забирает фишку из позиции p7, и “решающий” переход t2 выполниться не может. Таким образом, при p1=1 “решающий” переход недостижим.
На примере видно, что найти правильный ключ, т.е. правильную начальную маркировку, можно, перебрав всего лишь 24 = 16 значений. Это легко сделать даже вручную.
Использование ключей длиной менее 256 бит на сегодняшний день не может обеспечить защиту на достаточном уровне [4], именно поэтому простая сеть Петри из-за небольшого размера не годится для практической защиты.
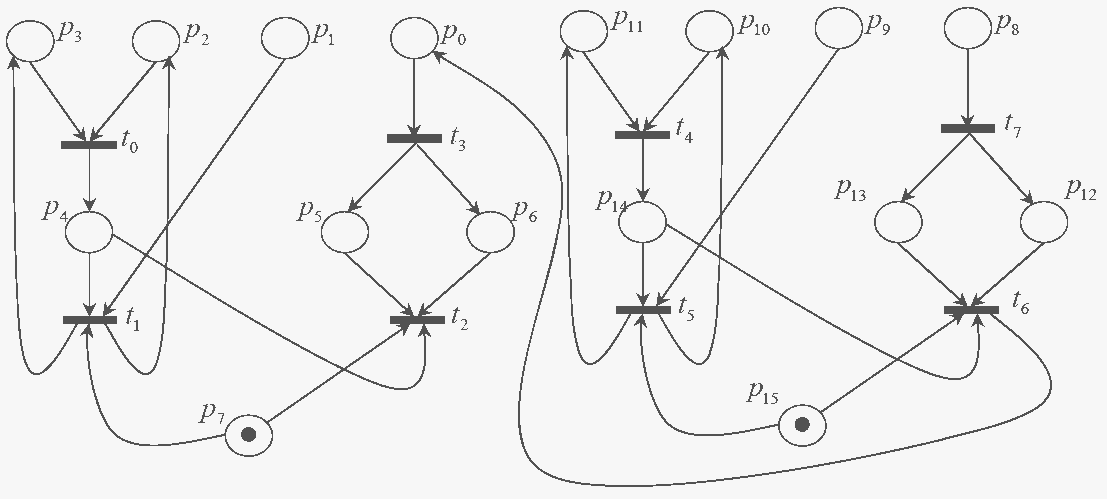
Для увеличения длины ключа при использовании в защите сетей Петри простую сеть предлагается наращивать, т.е. к каждой “начальной” ее позиции “подводить” новую сеть. При этом “начальные” позиции простой сети перестают быть доступными для начальной маркировки, но появляются новые N позиций в подведенной сети, доступные для начальной маркировки. Например, можно нарастить сеть над позицией p0, для чего достаточно просто скопировать уже имеющуюся (рис. 2).
Рисунок 2 - Усложненная сеть Петри При этом переход t2 остается “решающим”, и появляются новые позиции p8,…,p11, которые можно пометить при начальной маркировке и которые фактически дублируют смысловое значение позиций p0,…,p3 в первоначальной сети. Переход t6 фактически выполняет ту же роль, что и переход t2. Очевидно, что для срабатывания перехода t2 необходимо срабатывание перехода t6, а для этого начальной маркировкой необходимо пометить позиции следующим образом: p1=0, p2=1, p3=1, p8=1, p9=0, p10=1, p11=1.
Так как “начальных” позиций теперь 7, то длина ключа увеличилась до 27 бит, и для его идентификации с помощью полного перебора всех возможных значений ключей необходимо осуществить уже 27=128 проверок.
Надстроив аналогичным образом сеть Петри (см. рисунок 2) над p1, p2 и p3, получим ключ длиной 16 бит (добавляются 3·4=12 позиций и убавляется 3 позиции), для полного перебора необходимо рассмотреть уже 216 комбинаций, но этого также недостаточно для надежной защиты. Достаточным можно считать наращивание сети до обеспечения длины ключа 256 [4], в идеале — до 2128.
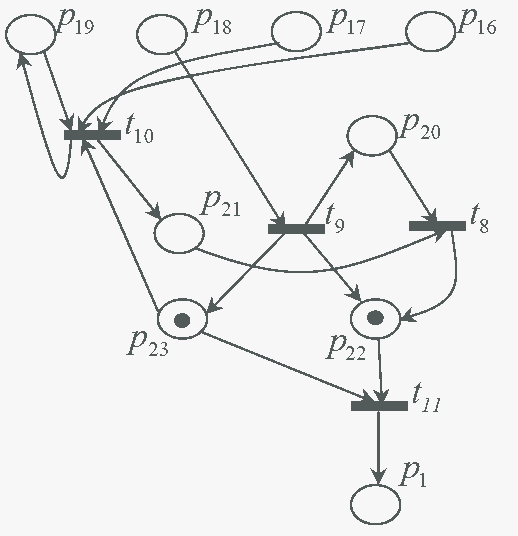
Теперь следует решить вопрос, будут ли сети, надстроенные над p0, p1, p2, p3, одинаковыми. Для простоты остановимся на 16 битном ключе. Единственная позиция, над которой нельзя нарастить сеть простым дублированием уже существующей, - позиция p1, т.к. для срабатывания t2 при вводе правильного ключа необходимо ее нулевое значение. Если нарастить над ней копию уже имеющейся сети, то нулевое значение позиции p1 достижимо при 15 (16-1) различных комбинациях. Это означает, что диапазон возможных ключей сужается. Поэтому для позиции p1 следует изменить надстроечную сеть (рис. 3).
Здесь, чтобы переход t11 не сработал, (то, чего нужно добиться), начальной маркировкой задаются следующие значения позиций: p16=1, p17=1, p18=0, p19=1.
Рисунок 3 - Вариант надстроечной сети для позиции P1 Переходу t11 необходимо задать наименьший приоритет.
Важным свойством матриц переходов является то, что их строки (столбцы) в защитном фрагменте программы можно переставлять в произвольном порядке, структура сети от этого не меняется, но усложняется анализ.
В общем случае для усложненной сети Петри исходная маркировка µ содержит биты ключа в позициях p0, p1,…,pk-1, где k - длина ключа, n - количество позиций в сети.
После того, как пользователь вводит правильный ключ для регистрации, запускаются переходы сети Петри несколько раз до достижения решающего перехода, и изменяется ее маркировка µ'. Если ключ неверен, то “решающий” переход не будет достигнут.
Для защиты необходимо создать такую сеть, в которой реализуется достижимость из µ в µ', если µ - это правильный ключ в позициях p0, p1, ..., pk-1. При этом сеть строится так, чтобы при ее работе с правильным ключом из маркировки µ не только могла, но и всегда получалась µ'. Кроме того, при любом другом ключе “решающий” переход не должен достигаться. Последнее реализуется с помощью приоритетов для переходов.
Рассмотрим надежность подобной защиты.
Если неизвестен способ защиты программы, то ключ можно найти полным перебором всех допустимых значений ключа (первый способ). Если известно, что для защиты использована сеть Петри, можно восстановить структуру сети по исходному коду защищенной программы, затем найти “решающий” переход, и в найденном месте сделать его обход с помощью, например, специальной программы (второй способ).
Если взломщик не делает обход, а создает генератор ключей (третий способ), то его задача - найти такую начальную маркировку µ сети Петри, из которой достижима маркировка µ', полученная после “решающего” перехода.
Однако в настоящее время в теории сетей Петри не решена задача определения маркировок µ, из которых достижима µ', кроме, естественно, запуска сети на выполнение для различных начальных маркировок и проверки.
Задача достижимости в теории сетей Петри имеет следующую формулировку: известны две маркировки для сети Петри - µ и µ'. Нужно определить достижимость µ' из µ.
Таким образом, задача сводится к многократному решению задачи достижимости, если решать ее для всех возможных начальных маркировок µ, при этом важны первые k позиций и позиции, содержащие при начальной маркировке фишки, количество фишек в остальных равно 0.
Решение этой задачи в генераторе (третий способ) можно организовать полным перебором всех возможных ключей по первому способу либо для ускорения взлома использовать существующие разработанные в теории сетей Петри методы определения достижимости.
В общем случае не решена и задача достижимости в приведенной формулировке, не найдены необходимые и достаточные условия для ответа на вопрос, достижима ли µ' из µ. Известны два подхода, которые определяют лишь необходимые условия достижимости: матричный подход и построение дерева достижимости [3].
При матричном подходе, если уравнение µ'=µ+xD, D+ и D– - матрицы входных и выходных функций сети Петри;
x - коэффициент, Для каждой µ нужно строить уравнение и, если решения в целых числах нет, отбрасывать такой ключ. А для оставшихся маркировок, для которых есть решение уравнения в целых числах, запускать фрагмент защиты. Решение приведенного уравнения в целых числах весьма сложная задача и может быть применимо, если будет занимать меньше времени, чем запуск фрагмента защиты.
Второй подход использует дерево достижимости для маркировки, которое содержит всевозможные маркировки µ', достижимые из µ. Дерево в генераторе ключа можно использовать следующим образом: если в ветке дерева есть искомая µ', значит это ключ. Алгоритм построения дерева достижимости [3] требует полного перебора маркировок µ' с помощью многократных запусков сети, т.е. время его работы не меньше времени работы фрагмента защиты для всевозможных начальных маркировок.
Таким образом, если ключ достаточно большой (более 56 битов), для его поиска нужно производить полный перебор всевозможных маркировок сети Петри, что свидетельствует о надежности защиты.
Для проверки и демонстрации предложенного метода защиты разработана программа, защищенная от взлома с помощью встроенной сети Петри. В защищаемом фрагменте использованы многопоточность для реализации запуска переходов и временные задержки для задания им приоритетов. Каждый переход - поток, который проверяет определенный набор битов на входе (входные позиции) и в зависимости от результата устанавливает набор битов на выходе (выходные позиции). Так, переход-поток t3 (см. рисунок 1) проверяет фишки (биты) в позиции p0 и в зависимости от того, есть фишка (бит установлен) или нет (бит сброшен), устанавливает биты в выходных позициях p5 и p6.
Предложенный метод защиты программного обеспечения дополняет известные методы защиты программ от отладки и в то же время имеет некоторые преимущества, прежде всего потому, что при работе защитного механизма используется многопоточность, что значительно усложняет отладку. Каждый поток реализует один переход сети Петри, а многопоточность для решения такой задачи, как выполнение сети Петри, естественна.
где D=D++D–;
не имеет решения, то µ' недостижимо из µ.
Список использованной литературы