Компьютеризированная система оптимизации потребления электроэнергии жилого дома
Авторы: Усова А.С., Хмелевой С.В.
Источник: Информатика и кибернетика Донецк, ДонНТУ – 2020 – № 1(19) – С.27–35
Аннотация
В статье рассмотрена актуальность проблемы оптимизации потребления электроэнергии, проанализировано использование методов Demand Response, произведён анализ стратегий формирования нагрузки, рассмотрены классификации электрооборудования, произведён анализ подходов для оптимизации потребления электроэнергии. Проведён обзор математических методов и алгоритмов, которые можно применить для исходной задачи. Выбран генетический алгоритм, проанализировано построение генетических алгоритмов применительно к Demand Response, проанализированы виды фитнес–функций для генетических алгоритмов, предложен вид генетического алгоритма применимый для исходной задачи с учётом заданных ограничений.
Ключевые слова:
Demand Response, генетический алгоритм, оптимизация работы электроприборов, оптимизация электроэнергии.
Введение
Потребление энергии представляет собой неотъемлемое условие существования человечества. С развитием человечества электропотребления увеличивается вместе с объёмом добычи ресурсов для обеспечения энергетической отрасли. Ученые подсчитали, что современные электростанции однажды не смогут удовлетворить спрос на электроэнергию, ведь ежегодное потребление растет в среднем на 15–20%. [1] Для того, чтобы в будущем избежать нехватку электрических мощностей во многих странах вводят программу Demand Response. Demand Response – это изменение потребления электроэнергии конечными потребителями относительно их нормального профиля нагрузки в ответ на изменение цен на электроэнергию во времени или в ответ на стимулирующие выплаты, предусмотренные чтобы снизить потребление в периоды высоких цен на электроэнергию на оптовом рынке или когда системная надёжность под угрозой [2]. Анализ литературных источников показывает, что существует целый класс проблем, относящихся к решению задачи Demand Response [3, 4].
Формы нагрузки на электроэнергию могут быть скорректированы с помощью следующих методов [5, 6]: peak clipping (отсечение пиков), valley filling (долина заполнения), load shifting (смещение нагрузки), load shifting (переключение нагрузки), energy efficiency (стратегическое сохранение), flexible load shape (гибкая форма нагрузки), см. рис. 1.
Рассмотрим подробнее каждую из них:
Peak clipping (отсечение пиков) – снижение нагрузки на коммунальные услуги в основном периоды пикового спроса.
Valley filling (долина заполнения) – улучшение коэффициента загрузки системы за счет наращивания нагрузки в непиковые периоды.
Load shifting (переключение нагрузки) – снижение нагрузки на коммунальные услуги в периоды пиковой нагрузки при одновременном наращивании нагрузки в непиковые периоды.
Energy efficiency (стратегическое сохранение) – сокращение коммунальных нагрузок, более или менее одинаково, в течение всего дня или большинства его часов.
Strategic load growth (стратегический рост нагрузки) – увеличение полезных нагрузок, более или менее одинаково, в течение всего или большинства часов дня.
Flexible load shape (гибкая форма нагрузки) – относится к программам, которые устанавливают опции коммунальных услуг для изменения потребления энергии потребителями по мере необходимости, как в соглашениях о прерывании или сокращении.

Рисунок 1 – Стратегии формирования нагрузки
Таким образом, load shifting (смещение нагрузки) является наиболее эффективным и широко используемым методом для управления нагрузкой в сетях электроснабжения жилого сектора.
Наиболее значительным объектом оптимизации в жилом секторе являются домашние электроприборы. Анализ приборов по виду и регулярности включения подразумевает некоторую классификацию. В рассмотренных источниках эта классификация различна. В частности, в [7] бытовые электроприборы рассматриваются с циклическим режимом работы и термостатическим управлением. В [8] авторы производят разделение электроприборов с циклическим режимом работы и неуправляемым режимом работы. В [9] классифицируются на электроприборы, работающие в присутствии человека в доме, которые нуждаются в управлении человеком и работающие без присутствия человека в доме. В [10] авторы выделяют следующие классы электроприборов: неконтролируемые приборы, управляемые электроприборы с бесперебойной нагрузкой, управляемые электроприборы с прерываемой нагрузкой. В [11] электроприборы делят на не оптимизирующийся электроприборы, электроприборы с термостатическим управлением и с циклическим режимом работы.
На основе вышеприведенной информации в рамках данной работы предлагается разделять электробытовые приборы на следующие категории:
- не оптимизирующийся;
- с термостатическим управлением;
- с циклическим режимом работы;
- нуждающиеся в присутствии человека в доме.
Анализ литературных источников показывает, что оптимизация приборов с термостатическим управлением и приборов с циклическим режимом работы возможна и широко применяется рядом авторов.
Постановка задачи
Классической целью подобных работ является минимизация расходов на электроэнергию, кроме этого, в работах [12–15] учитываются ограничения пиковой нагрузки, для которой может быть применён один из вышеупомянутых методов (рис. 1).
Имеются M – квартир в доме, и N – электроприборов в каждой квартире. Для каждого управляемого электроприбора задаются пользователем ti – время включения i–ого электроприбора, где i = [1, … , N] и Δti – длительность времени работы электроприбора.
Отсюда время окончания работы электроприбора: t’i = ti + Δti
Для каждого из электроприборов можно получить функцию оценки мощности для i–ого электроприбора – Pi.
Для i–ого электроприбора функция оценки мощности за сутки будет равняться сумме мощностей каждого из включений, которые зависят от времени включения электроприбора и длительности времени работы электроприбора. Следовательно, можно получить следующую формулу: Pt=∑tPi(ti,Δt )
Для того, чтобы получить общую мощность P необходимо найти сумму всех Pt: Pt=∑Pt
Стоимость потребляемой электроэнергии обозначим S. Стоимость для i–ого электроприбора в сутках будет равняться сумме стоимостей электроэнергии для каждого из запусков в разное время суток: St=∑tSi(Pi(ti,Δt),ti)
Стоимость электроэнергии не является константой и может меняться в различное время суток (т.н. ночной тариф).
Для того, чтобы получить общую стоимость потреблённой электроэнергии S, необходимо найти сумму всех стоимостей по всем запускам электроприбора St: S=∑St:
Целью работы является минимизация суммарных затрат на электроэнергию с учетом дневного и ночного тарифа: S → min
Это достигается благодаря смещению времён включения электроприборов. Таким образом, чтобы максимальное время соседних включении было меньше, чем максимальное время ограничения выключения электроприбора: max(ti – ti+1) < tmax
Методы, применяемые для оптимизации
В изученных источниках для оптимизации потребления электроэнергии использовались следующие методы: метод роя частиц (BPSO), алгоритм решения задачи линейного программирования методом внутренней точки, генетический алгоритм (ГА), жадный алгоритм.
В методе роя частиц (BPSO) каждая частица представляет потенциальное решение проблемы. Поведение частицы в гиперпространстве поиска решения все время подстраивается в соответствии со своим опытом и опытом своих соседей. Каждая частица помнит свою лучшую позицию с достигнутым локальным лучшим значением фитнес–функции и знает наилучшую позицию частиц – своих соседей, где достигнут глобальный на текущий момент оптимум. Данный метод был применён авторами в [10]. В работе представлена стратегия управления спросом, основанная на методе планирования нагрузки электросети на день вперед. Планирование домашних устройств приведено таким образом, чтобы исключить пиковые значения потребления электроэнергии и минимизировать счета за электроэнергию. Частица представляет собой двумерный массив из 0 и 1. Строчки, в которых представляют отдельные электроприборы, столбцы – номер часа. 0 – выключение электроприбора в заданный час, 1 – включение. Частица развёртывается в вектор: S = [S1, S2, S3, …, S23, S24].
Линейное программирование – это методы решения экстремальных задач на множествах n–мерного векторного пространства, задаваемых системами линейных уравнений и неравенств. Согласно методам внутренней точки исходную для поиска точку можно выбирать только внутри допустимой области. При этом множество точек делится на допустимые и недопустимые в зависимости от ограничений. Множество допустимых точек в зависимости от ограничений также делится на граничные и внутренние. Авторы в [11] рассматривают задачу оптимизации энергопотребления домохозяйства, без альтернативных источников энергии, путем построения оптимального графика использования бытовых приборов. По классификации, предложенной в [16], эта задача сводится к основной задаче целочисленного программирования и предлагается алгоритм ее решения методом внутренней точки. Целевая функция исходной задачи определяется как суммарная стоимость потребленной энергии. Оптимизируются моменты включения и выключения приборов в рамках разбиения на номера временных интервалов, осуществленных заранее.
В жадном алгоритме процесс принятия решения можно разбить на элементарные шаги, на каждом из которых принимается отдельное решение. Решение принимаемое на каждом шаге должно быть оптимальным только на текущем шаге и должно приниматься без учета предыдущих или последующих решений. Данный алгоритм разделяет задачу на меньшие подмножества той же проблемы. Авторы в [17] рассматривают обширные стратегии управления спросом с использованием жадного алгоритма. В работе анализируется планирования потребления электроэнергии бытовыми приборами в домашней сети. Цель предлагаемого планирования состоит в том, чтобы минимизировать общие расходы на электроэнергию для потребителя и сбалансировать нагрузку сети.
Генетический алгоритм – адаптивный метод поиска, который используются для решения задач функциональной оптимизации. Основан на механизмах и моделях эволюции, и генетических процессов биологических алгоритмов.
В данной работе предлагается оптимизировать потребления электроэнергии с помощью генетического алгоритма.
Генетические алгоритмы применяются для решения задач Demand Response большим количеством авторов [15], [17–21]. Генетический алгоритм применяют для минимизации денежных затрат на электроэнергию для домашних хозяйств [12–14], для офисных секторов [13], для промышленных [14]. ГА применяют для снижение пиковой нагрузки на электросеть [14–17], [18]. Также для оптимизации расхода электроэнергии могут применяться различные ограничения [12], [15], [18], в частности, учтён комфорт пользователя (по времени включения электроприборов) [15], [18]. Полученные результаты моделирований в приведённых выше работах показывают, что ГА эффективен в поставленной задаче.
Предлагаемое решение
В данной работе предполагается, что в многоквартирном доме, в условиях ОСМД, устанавливается в каждой квартире микроконтроллер, который будет управлять электроприборами. При этом оплата за электроэнергию начисляется по двум тарифам: ночному и дневному. В свою очередь пользователи дают информацию администратору о электроприборах, которые будут регулироваться. А именно, наименование электроприбора и его потребляемую мощность. Также пользователи составляют расписание (часы работы) для своего электрооборудования в квартире. В свою очередь компьютеризированная система будет распределять время работы для электроприборов с термостатическим управлением и с циклическим режимом работы.
Поэтому в данной работе для решения поставленной задачи будет применён генетический алгоритм. Блок–схема алгоритма представлена на рис. 2.

Рисунок 2 – Блок–схема генетического алгоритма
Как видно из рис. 2 для определения генетического алгоритма необходимо задать следующие параметры: способ кодирования, генетические операторы (кроссинговер, мутация, репродукция), задание фитнес–функции.
Практически во всех изученных источниках [12–15], [17], [19] кодирование хромосомы применялось одинаковое, а именно хромосомы рассматриваются как массив битов, которые представляют состояние включения (равно 1) или выключения (равно 0) электроприборов.
Предлагаем использовать следующую кодировку [15] каждая хромосома состоит из восьмибитового шаблона, так что каждое устройство использует определенный битовый шаблон, относящийся к его идентификатору класса, идентификатору устройства, биту планирования, прерываемому или не прерываемому биту и биту приоритета. На основе рабочего состояния устройства отслеживается его почасовая стоимость. В каждом классе каждый атрибут использует один бит, за исключением идентификатора класса и расписания устройства, которые используют трёхбитные и двухбитные шаблоны соответственно, см. рис. 3.
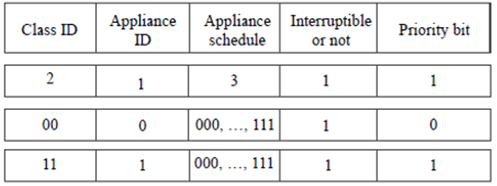
Рисунок 3 – Кодирование хромосом
Поскольку в исследуемой работе используется стандартный генетический алгоритм практически во всех источниках, генетические операторы – стандартные двоичные кроссинговер, мутация, классическая репродукция.
Рассмотрим параметры генетический алгоритмов. Вероятность скорости кроссинговера является очень важным управляющим параметром и напрямую зависит от скорости конвергенции. Большое значение скорости пересечения означает быструю сходимость за счет точности. В [20] упоминается, что в литературе установлено наилучшей скоростью кроссинговера для задачи оптимизации является: Pc = 0.9. А для того, чтобы избежать повторений в популяции, авторы используют процесс мутации. Он изменяет один или несколько генов в хромосоме от ее начального состояния. Вероятность мутации очень мала, что определяется следующей формулой:Pm=1–Pc / 10
Из этого следует что большая скорость кроссинговера означает более быструю сходимость, а большая скорость мутации означает потерю хорошего решения и вызывает преждевременную сходимость алгоритма. Таким образом, для достижения лучших результатов вероятность скорости кроссинговера высока, а частота мутаций низка.
В [21] кроссинговер имеет несколько типов: точечный, многоточечный и равномерный. А также рассматривается вид репродукции методом колеса рулетки. В [14] используются точечный кроссинговер и бинарная мутация. Также применяется элитизм для запоминания наилучшего решения и передается от одного поколения к другому. Отбор на основе турнира используется для формирования новой популяции из существующих, и алгоритм завершается при выполнении критериев генерации.
В ГА используются четыре основных метода для учета накладываемых ограничений при решении оптимизационных задач. Простейшим способом является метод отклонения (отбрасывания), где недопустимые хромосомы (не удовлетворяющие ограничениям) исключаются из дальнейшей эволюции, такой способ рассматривается в [12], [18]. Второй метод основан на использовании процедуры восстановления, которая преобразует полученное недопустимое решение в допустимое (в рамках данного обзора работ найдено не было). Третьим методом является применение проблемно–ориентированных генетических операторов, которые порождают только допустимые решения (не применим в рассматриваемой задаче). И четвертый способ – применение штрафных составляющих к фитнес–функции, данный способ рассматривается в [15].
Генетический алгоритм был применён во многих исследовательских работах для оптимизации потребления электроэнергии, в каждой работе были выведены свои фитнес–функции рассмотрим подробнее каждую из ник.
В работе [19] применена фитнес–функция общей стоимости энергопотребления за интервал планирования стремящаяся минимизировать суммарные затраты на электроэнергию:
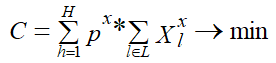
Где:
С – суммарная стоимость электроэнергии;
Xlh – запланированное потребление энергии прибором;
l – нагрузка электроприбора, где l ∈ L;
L – запланированная нагрузка на сутки;
h – единица времени, продолжительность h=1 час, h ∈ H;
H – горизонт планирования, где H = 24 часа.
ph – тариф на электроэнергию в каждый час.
В [15] фитнес–функция общей стоимости энергопотребления стремится минимизировать суммарные затраты на электроэнергию с учётом штрафных ограничений.
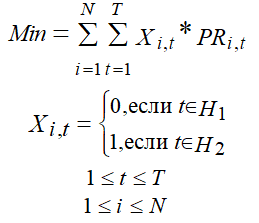
Где:
Xi,t – текущее состояние электроприбора, Xi,t = 1 – включен, если Xi,t = 0 – выключен;
PRit – стоимость электроэнергии, потребленной в течение любого интервала времени t, который является показателем времени, верхнего предела T (T = 24) часа в сутки;
H – представляет собой горизонт планирования работы электроприборов, время 24 часа в сутки, включая PHs (пиковые часы) и OPHs (непиковые часы). H = {1,2,…,T}. При этом H1 = {7,8,9,10} включает PHs часы, H2 = {H / H1} – OPHs;
i – обозначает порядковый номер электроприбора, который принимается как N – число оптимизирующийся электроприборов.
В работе [15] применяются раннее рассмотренные штрафные составляющие к фитнес–функции. Расписание работы электроприборов моделируется с точки зрения минимальной задержки электроприборов и оптимальных сумм оплаты за электроэнергию. Рассмотрим подробнее, в этом примере максимизируют экономию электроэнергии и комфорт пользователя. Для минимизации разочарованности пользователей вводится приоритетность электроприборов. Приборы с высоким приоритетом планируются в первую очередь через доступные интервалы непиковых часов. Включение оборудования с низким приоритетом может быть отменено или отложено вовремя пиковый часов. Таким образом, время ожидания приборов сводится к минимуму, а комфорт пользователя достигается максимально. Получаем следующие уравнения:

Где:
EcostSavings – сэкономленная электроэнергия;
EappUtill – полезность бытовой техники (на сколько пользователю удобна работа прибора в конкретное время, измеряется от 0 до 1);
α и β – переменные задержки. Согласно ограничению, сумма α и β равна единице, поскольку комфорт пользователя колеблется между нулем и единицей;
delay – функция задержки, и в исходном сценарии она ограничена 4 часами. Следует отметить, что эти 4 часа выбираются из пиковых часов для уточнения максимальной задержки приборов.
cost – это функция стоимости, и ее значения находятся между 20% и 70%. Ниже 20%, его значения не принимаются в расчёт, стоимость незначительна; и более 70% стоимости используются для микросетей.
Sch_сost – стоимость приборов в течение всего дня. Рассчитывается по битам состояния устройства x номинальная мощность;
Max.сost – стоимость пиковых часов дня.
Значения α, β, delay, Sch_сost берутся из работы [9].
Учитывая вышеперечисленные критерии, фитнес–функция имеет следующий вид:

Где: с1 = с2 = 0.05
В данной фитнес функции сохраняются все вышеперечисленные ограничения.
В [12] фитнес–функция стремиться минимизировать общие затраты на электроэнергию. Общая стоимость, TC за весь период планирования является суммой комбинации пиковых и внепиковых затрат каждой i–той задачи:
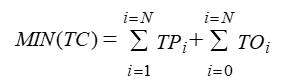
Где:
TC – общие затраты на электроэнергию, кВт;
TP – стоимость работы оборудования в пиковые часы;
TO – стоимость работы оборудования в непиковые часы;
i – индекс задачи;
N – количество управляемого электрооборудования.
В данной работе ограничения осуществляются раннее рассмотренным методом отклонения. В процессе оптимизации выполняются следующие ограничения:
- баланс нагрузки системы: поскольку существует предел мощности нагрузки в цепи, в любое время t, общая нагрузка системы(Ri) не может быть выше LM. LM – максимальная нагрузка мощности в доме:
- существует ограничение времени запуска для каждой задачи:
- существует ограничение времени завершения для каждой задачи:
- задача, которая уже была запущена, не может быть вытеснена другими задачами в расписании.
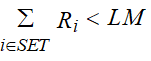

Где:
SSi – запланированное время начала выполнения i задачи;
Si – самое раннее время начало i задачи.
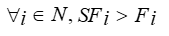
Где:
SFi – запланированное время завершения i задачи;
Fi – самое позднее время окончания i задачи.
К заданной задаче раннее приведённые примеры являются малоприменимы, так как рассматривается оптимизация потребления электроэнергии только жилого сектора, при этом в исследуемой задаче всего два тарифа стоимости электроэнергии – дневной и ночной тарифы. А также рассматривается пиковая нагрузка, которая будет влиять на оптимизацию фитнес–функции.
Снижение пиковой нагрузки потребления электроэнергии предлагается решать методом load shifting: ∀max(Pi) < limit
В связи с этим вводится понятие приоритета электроприборов – Pr. Приоритет электроприборам назначается по их классификации:
- приоритет неуправляемых электроприборов: Pr = 1;
- приоритет электроприборов с термостатическим управлением: Pr = 2;
- приоритет электроприборов с циклическим режимом работы: Pr = 3.
Таким образом, наименьшее значение приоритета, при котором Pr = 1 имеет наивысший приоритет.
Внутри групп классификаций каждому электроприбору назначается приоритет.
Введём следующее ограничение: если суммарное потребление мощности электроприборов превышает значение максимальной мощности, то среди всех включённых электроприборов отключается электроприбор с наименьшей приоритетностью:
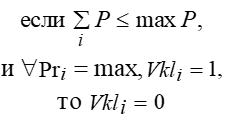
Где:
Vkli – это текущее состояние электроприбора. Vkli = 1 – включен, Vkli = 0 – выключен.
Вышеприведённые ограничения, в частности приоритет электроприбора предлагается свести к ограничениям комфорта пользователя, как в работе [9], а именно:
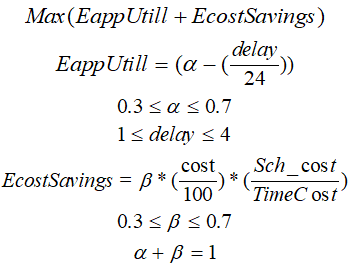
Где:
α и β – переменными задержки;
EcostSavings – сэкономленная электроэнергия;
EappUtil – полезность бытовой техники (на сколько пользователю удобна работа прибора в конкретное время, измеряется от 0 до1);
delay – функция задержки, и в исходном сценарии она ограничена четырьмя часами;
cost – это функция стоимости, и ее значения находятся между 20% и 70%. Ниже 20% значения не принимаются в расчёт, стоимость незначительна; и более 70% стоимости используются для микросетей;
Sch_cost – стоимость мощности приборов в течение всего дня, рассчитывается по битам состояния устройства x, номинальная мощность;
T – горизонт планирования, T = 24;
Значения α, β, delay, Sch_сost берутся из [9].
С учётом вышеприведённого анализа, предлагаем следующую реализацию фитнес–функции, которая будет стремится минимизировать затраты на электроэнергию:
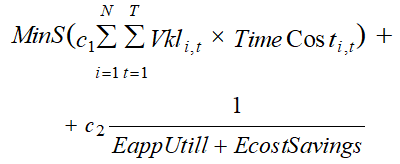
Где:
i – индекс электроприбора;
N – количество электроприборов;
Vkli,t – текущее состояние электроприбора, если Vkli,t = 1 – включен, если Vkli,t = 0 – выключен;
TimeCosti,t – текущая стоимость электроэнергии, потребленной в течение любого интервала времени t, t∈T.
T – горизонт планирования, T = 24;
EcostSavings – экономия электроэнергии выраженная в процентах;
EappUtill – полезность бытовой техники (на сколько пользователю удобна работа прибора в конкретное время, измеряется от 0 до1);
с1 = с2 = 0.05.
В полученной фитнес–функции размер штрафных ограничений сопоставим с размером энергопотребления самой фитнес–функции.
По проведенному анализу получаем следующий псевдокод для оптимизации потребления электроэнергии многоквартирного дома, с заданными ограничениями. Алгоритм представлен на рис. 4.

Рисунок 4 – Алгоритм псевдокода для ГА
По предложенному псевдокоду достаточно просто выполнить программную реализацию позволяющую оптимизировать энергопотребление многоквартирного дома с учётом ограничений по максимальному пиковому энергопотреблению.
Выводы
В данной работе по оптимизации потребления электроэнергии жилого дома проанализировано использование методов Demand Response, из заданных методов выбран генетический алгоритм по следующим причинам:
- прост и прозрачен в реализации;
- присутствуют хорошие параллельные возможности;
- быстрее и эффективнее по сравнению с традиционными методами;
- отличается эффективностью, когда пространство поиска очень велико и задействовано большое количество параметров.
Проанализировано построение генетических алгоритмов применительно к Demand Response, проанализированы виды фитнес–функций для генетических алгоритмов, предложен вид генетического алгоритма применимый для исходной задачи с учётом заданных ограничений.
REFERENCES
- Зачем надо экономить электроэнергию [Электронный ресурс] // Ася Малютина. – Электрон. текст. – [Россия, 2015]. – Режим доступа: https://recyclemag.ru/article/zachem-nado-ekonomit-elektro– Загл. с экрана.
- National Assessment & Action Plan on Demand Response – 2016 – Режим доступа:https://ru.wikipedia.org/wiki/Управление_спросом_на_электроэнергию#cite_note-1– Загл. с экрана.
- Na Li, Lijun Chen and Steven H. Low Optimal Demand Response Based on Utility Maximization in Power Networks Power and Energy Society General Meeting // IEEE Power and Energy Society General Meeting, 2011. – p.1–8.
- Dehnavi E, Abdi H. Optimal pricing in time of use demand response by integrating with dynamic economic dispatch problem // Energy 109, 2016. – p.1086–1094.
- Kishor C. Muley, Sandeep Bhongade Load Management Techniques and Pricing Model for Demand Side Management // International Journal on Emerging Technologies 10(1) 2019. – p.42–46.
- Mohamed AboGaleela, Magdy El–Marsafawy, Mohamed El–Sobki Optimal Scheme with Load Forecasting for Demand Side Management (DSM) in Residential Areas // Energy and Power Engineering, Vol.5, 2013. – p.889–896.
- Lujano–Rojas JM, Monteiro C, Dufo–López R, Bernal–Agustín JL. Optimum residential load man–agement strategy for real time pricing demand response programs // Energy policy, Vol.45, 2012. – p.671–679.
- Bradak Z., Kaczmarczyk V., Fiedler P. Optimal scheduling of domestic appliances via MILP // Energies, Vol.8, Iss. 1. 2015. – p.217–232.
- Mahmood, D.; Javaid, N.; Alrajeh, N.; Khan, Z.A.; Qasim, U.; Ahmed, I.; Ilahi, M. Realistic scheduling mechanism for smart homes // Energies Vol. 9, 2016, – p.202.
- Kumar, K.S.S., Naik, M.G.: Load Shifting Technique on 24Hour Basis for a Smart–Grid to Reduce Cost and Peak Demand Using Particle Swarm Optimization // IRJET, Vol.04, 2017. – p.1180–1185.
- Гребенюк Г.Г., Крыгин А.А. "Оптимизация энергопотребления домохозяйства на основе прогноза графика максимальной нагрузки бытовых приборов." – Управление большими системами: сборник трудов 69, – 2017.
- H. Miao, X. Huang, G. Chen. A Genetic Evolutionary Task Scheduling Method for Energy Efficiency in Smart Homes // International Review of Electrical Engineering (I.R.E.E.), Vol.7, N 5, 2012 – p.5897–5904.
- Nusrat Shaheen, Nadeem Javaid, Najmun Nisa, Amber Madeeha Zeb, Zahoor Ali Khan, Umar Qasim. Appliance Scheduling for Energy Management with User Preferences // International Conference on Innovative Mobile and Internet Services in Ubiquitous Computing 10th. 2016. – p.328–334.
- M. Awais, N. Javaid, N. Shaheen1, Z. Iqbal, G. Rehman1, K. Muhammad, I. Ahmad. An Efficient Genetic Algorithm Based Demand Side Management Scheme for Smart Grid // COMSATS Institute of Information Technology. 2015. – p.351–356.
- Javaid N., Javaid S., Abdul W., Ahmed I.; Almogren, A., Alamri, A., Niaz, I.A. A Hybrid Genetic Wind Driven Heuristic Optimization Algorithm for Demand Side Management in Smart Grid // Energies, Vol.10, N 319, 2017, – p.1–7.
- Albadi M.H., El–Saadany E.F. A summary of demand response in electricity markets // Electric Power Systems Research, Vol.11, Iss. 78, 2008. – p.1989–1996.
- Cui, Tiansong, Hadi Goudarzi, Safar Hatami, Shahin Nazarian, and Massoud Pedram. Concurrent optimization of consumer's electrical energy bill and producer's power generation cost under a dynamic pricing model // IEEE PES Innovative Smart Grid Technologies (ISGT), 2012. – p.1–6.
- R. R. El–Razky, A. A. Daoud and . K. El–serafi, Optimization of Residential Load Consumption during Energy Peaks using Smart Metering // Renewable Energy and power quality journal (RE&PQJ), Vol.1, N 15, 2017. – p.227–232.
- Oladeji, O., Olakanmi, O. O. A genetic algorithm approach to energy consumption scheduling under demand response // IEEE 6th International Conference on Adaptive Science & Technology (ICAST), 2014.– p.1–6.
- Mudassar Naseem, Nadeem Javaid Heuristic Algorithm based Home Energy Management System in Smart Grid. In “Electrical Engineering COMSATS Institute of Information Technology Islamabad” – 2016. – Pakistan, p.15–63.
- Urva Latif, Nadeem Javaid, Syed Shahab Zarin, Muqaddas Naz, Asma Jama, Abdul Mateen. Cost Optimization in Home Energy Management System using Genetic Algorithm, Bat Algorithm and Hybrid Bat Genetic Algorithm // IEEE 32nd International Conference on Advanced Information Networking and Applications 1550–445X/ 2018. – p.667–677.