An Efficient Genetic Algorithm Based Demand Side Management Scheme for Smart Grid
Author: M. Awais, N. Javaid, N. Shaheen, Z. Iqbal, G. Rehman1, K. Muhammad, I. Ahmad
Source: COMSATS Institute of Information Technology. 2015. – p.351–356.
Abstract
In this paper, we propose a novel strategy for a Demand Side Management (DSM) in a Smart Grid (SG). In this strategy, three types of loads are considered, i.e., residential load, commercial load and industrial load. The larger number of appliances of different power rating for each type of load is considered in this work. The focus of this work is to minimize the Peak to Average Ratio (PAR) to increase the efficiency of SG, by increasing the utilization of spinning reserves. On the other hand, our aim is to minimize the electricity consumption cost. Tackling the large number of appliances in an SG is a challenging task, because it increases the complexity of the problem. However, in literature the focus is on small number of appliance. In this work, the load scheduling problem is mathematically formulated and solved by using genetic algorithm. The simulation results show that the propose algorithm reduces the cost, while reducing the peak load demand of the SG.
Index Terms
Genetic algorithm; Appliance scheduling; Smart grid; Energy management; Demand side management.
I. INTRODUCTION
Smart Grid (SG) is the integration of communication and control technologies in a traditional grid in order to transmit and distribute electricity in an efficient way. The purpose of this transformation is to reduce global warming by reducing carbon emission and reduce electricity cost by efficiently manage the load. Demand Side Management (DSM) is an important feature of SG to manage energy. The goal of DSM is to efficiently utilize the available grid energy to improve the economics of the power system. Managing the load pattern can reduce the peak load demand which improves efficiency of grid, reduce the carbon emission and electricity bill of the user.
Dynamic pricing schemes are the unique features of the SG. By usage of smart meters and automatic metering infrastructure, it is easy to manage the load according to dynamic pricing schemes. Some of the dynamic pricing schemes which commonly used in DSM programme are Real Time Pricing (RTP), Time of Use (TOU), Critical Peak Pricing (CPP), Day Ahead Pricing (DAP) and Extreme Day Pricing (EDP). When these dynamic pricing schemes are used along with the DSM strategies, control of customer energy usage is influenced by penalties and incentives. However, the rationale behind DSM is to increase power system stability, sustainability, security and economics by maximizing system capacity without changing whole physical infrastructure of the power system.
DSM also plays a key role in the electricity market. Electricity price is depends on the energy consumption of the users. With exceeds in demand the price is also vary and increase. This increase in electricity pricing affects whole users in the power system. By reducing the Peak to Average Ratio (PAR), DSM regulates the electricity price in an electricity price market.
DSM modify the customers’ demand pattern to get the desire change in load shape of power network. The DSM strategies modify the shape of load pattern by shifting the controllable appliances during peak hours, and shifts these loads to an appropriate time to reduce the cost.
There have been six methods for load shaping of different types of users [1–3]: peak clipping, valley filling, load shifting, flexible load shape, strategic conversation and strategic load growth. Peak clipping and valley filling reducing the difference between peak load and valley load by filling the valley from a curtail load from the peaks to reduce the load burden. While, strategic conversation [1], reduce the peak load demand at customer premises. Strategic load growth[1–3] introduce large demand in the valley in off–peak to produce optimized load curve. Flexible load shape [1–3], only modify the demand curve of the customers which are willing to take part in the DSM program in exchange for incentives. Whereas, load shifting [3] is generally used to shift load from on–peak to off–peak in order to minimize the cost.
In this work, we proposed a DSM strategy based on load shifting technique. Several types of large number of appliances are considered in this work to show the effectiveness of the proposed algorithm. In [4], the load shifting problem is solved using GA to reduce the cost and PAR. We solve the same problem as in [4], with a different load shifting strategy to get better results than the previous one. For this we formulate the load shifting problem as a cost minimization problem with some constraints to achieve electricity bill and PAR reduction.
II. RELATED WORK
In recent many DSM strategies have been proposed. The primary objective of these techniques is cost minimization and reduction in peak load demand.
Evolutionary algorithm is used to schedule different types of large number of appliances in [4]. This algorithm brings the user load curve near the objective curve, which is reciprocal to the given electricity price signal. Various types of loads are tackling in this work, i.e., residential, commercial and industrial loads. Results show that this method is efficient as compared to mathematical approaches in tackling a large number of loads.
In [5], author proposed an Integer Linear Programming (ILP) based appliance scheduling scheme to shift the load from on–peak to off–peak to reduce electricity consumption expense and peak load reduction. The architecture of DSM is presented in [6]. This proposed architecture integrate renewable energy in the power system to minimize the monitory expense of the user.
Linear Programming (LP) based cost efficient Optimization–based Residential Energy Management (OREM) scheme is proposed in [7], to minimize overall cost and PAR. Mono–tonic optimization based DSM strategy is proposed in [8], mathematical modeling of the centralized renewable energy source has been done to demonstrate the optimal utilization of the renewable energy. A Mixed Integer Linear Programming (MILP) [9], formulation is used for scheduling various types of appliances to reduce the electricity bill of the user.
A strategy to avoid distribution system overloading is proposed in [10], an algorithm is proposed which checks the priority of appliance and shut down it to avoid distribution system overloading. As an example, large penetration of electric vehicles and its effect is discussed. Distribution system over–loading is avoided by proper load shedding. Optimal Stopping Rule (OSR) based appliance scheduling scheme is proposed in [11]. It is a mathematical optimization technique which gives the time where the price is low, so user schedule its appliance at that time. This reduces the electricity consumption cost.
Stochastic optimization based cost minimization problem along with the integration of renewable energy is proposed in [12]. The cost minimization problem is solved using LYAPUNOV optimization approach. A strategy which integrates renewable energy in the power system to increase the efficiency of network is proposed in [13], user minimize its monitory expenses by selling/purchasing grid energy.
Most of the techniques mentioned above was developed using ILP, LP, MILP and OSR cannot handle a large number of appliances which have different consumption pattern due to the complexity of the problem. Furthermore, loads are spread over a few hours, i.e, the duty cycle of each type of load is different. In this regard, GA algorithm is able to handle all these parameters in a efficient way as compared to other mathematical strategies.
The rest of this paper is organized as follows. Section II gives problem formulation, Proposed DSM algorithm is presented in section IV, SG detail is described in section V, simulation detail provides in section VI and VII concludes the paper.
III. PROBLEM FORMULATION
In this section, the load scheduling problem is formulated as a minimization problem. Due to intermittent nature of the electricity market, we assume that the RTP signal change on one hour basis and its value is constant within one hour. Our objective is to minimize the electricity bill of user as well as reduce the PAR to increase the efficiency of the grid. The minimization problem is formulated as follows.
Minimize

Subject to

t Time slots.
a Number of appliance.
b Type of appliance
Eab Energy consumption of appliance a of type b.
EP(t) Electricity price at time slot t.
xab ON/OFF State of appliance a of type b.
ma Maximum permissible delay of appliance b.
la Number of ON request of appliance, i.e., length of operation time.
L(t) Maximum power limit at time slot t.
Yab Controllable appliance a of type j.
A(t) Set of controllable appliances at time slot b.
Equation 2 represents that energy consumption at time slot t is less than maximum limit to reduce the PAR. Maximum permissible delay for each appliance is represented by equation 4. Equation 5 shows that appliance a of type b cannot be schedule further after completing its length of operation time. Moreover, equation 6 tells us that the number of appliances participate in scheduling cannot be in negative. Furthermore, the number of appliances a of type b, shifted cannot be greater than the number of controllable appliances at time slot t is represented by equation 6, i.e, DSM controller only schedule controllable devices not all appliances in the system.
IV. PROPOSED ALGORITHM FOR DSM
This proposed algorithm managing power consumption of large number of controllable appliances belongs to differ– ent categories in the SG. Each type of load have different consumption pattern and different length of operation time. Therefore, the design scheme should be able to tackle all these involutions. However, many proposed techniques in literature commonly used for scheduling, i.e, LP, OSR and dynamic programming, but these techniques cannot handle such a large number of appliances due to complexity. Evolutionary algorithm such as GA have potential to solving these types of complex problems. GA provide near optimal solution of the given problem. Hence we use GA based scheduling algorithm to solve cost optimization problem. In this scenario, appli– ances request to DSM controller for connection permission. The DSM controller cumulatively deals with the appliances in each time slot, and give a complete pattern by solving the minimization problem. The DSM is carried out at the beginning of the day, and when an appliance sent a request to DSM controller, it takes action on the basis of DSM technique results which carried out in advance.
The chromosomes pattern of GA represent the solution. In this research work, chromosomes are considered as an array of bits which represent the ON/OFF state of appliances. Thus, the length of chromosomes depends on the number of controllable appliances.
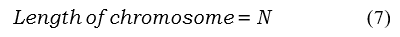
where, N is the number of controllable loads in each area. The population of chromosomes is randomly initialize after that a fitness function is evaluated. In this case, a fitness function is evaluated by using the eq. 1.
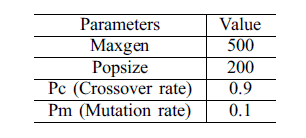
The steps of GA for solving minimization problem are shown in Fig. 1. In each iteration new population of chromosomes are produced by crossover and mutation. Single point crossover and binary mutation are used in this work. The convergence of the algorithm depends upon the crossover and mutation rate. Larger crossover rate means faster the convergence and larger mutation rate means loss of good solution, and cause premature convergence of the algorithm. Sometimes, near optimal solution is found early on in GA but get missed by crossover and mutation. One best solution is remembered from the population. Elitism is used to remember this solution and carried forward from one generation to the next one. GA parameters are shown in Table 1. A tournament based selection is used to form a new population from the existing ones, and the algorithm is terminated when generation criteria are met. The DSM algorithm is as follows.
TABLE I PARAMETERS OF GA
V. DETAIL OF THE SG
To demonstrate the effectiveness of the proposed scheme, the algorithm is tested three different areas of the SG. The primary objective of this work is to reduce the electricity

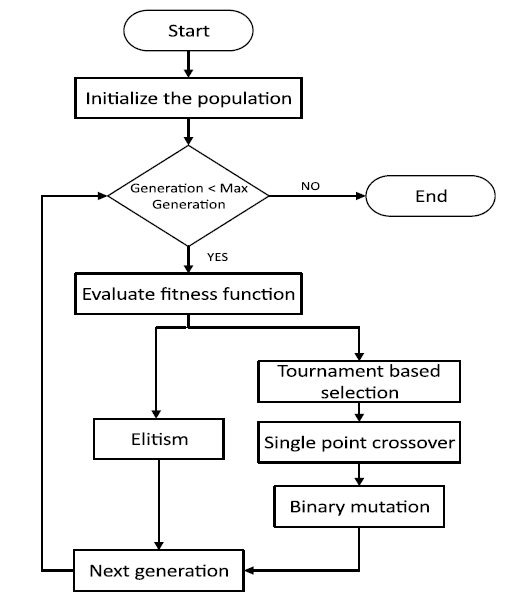
Fig. 1. Main steps of algorithm
consumption cost and the secondary objective is to reduce the PAR. Each area of the SG has different types of controllable loads, details of these areas is given as follows.
A. Residential Area
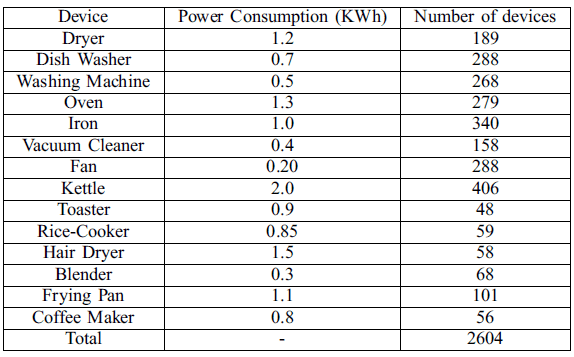
In this case, residential area contains more than 2600 controllable appliances of 14 different types with different power rating. Generally, residential area load has low power consumption rating and small duty cycle. Different types of appliances of residential area with their power rating are given in table 2.
TABLE II CONTROLLABLE DEVICES IN RESIDENTIAL AREA
B. Commercial Area
Commercial area contains more than 800 controllable appliances of 8 different types with different power rating. Commercial area load has a power consumption rating higher 10 than the residential area. Different types of appliances of the commercial area with their power rating are given in table 3.
TABLE III CONTROLLABLE DEVICES IN COMMERCIAL AREA

C. Industrial Area
Industrial area contains more than 100 controllable appliances of 6 different types with different power rating. Industrial area load has higher power consumption and long consumption period among all areas. The available controllable devices in industrial area is less, reason is that the industrial load is sensitive and cannot be allowed to load control. Different types of appliances of industrial area with their power rating are given in table 4.
VI. SIMULATION RESULTS
In this section simulation results are discussed. Simulations results show that the proposed DSM scheme efficiently manage large number of controllable loads in all three areas. The proposed algorithm shifts the load to minimize the cost and PAR.
Pricing scheme for all types of users is same in SG. The RTP signal is shown in Fig. 2. Simulation results from the residential area is shown in Fig. 3. Residential users
TABLE IV CONTROLLABLE DEVICES IN INDUSTRIAL AREA

Fig. 2. RTP signal
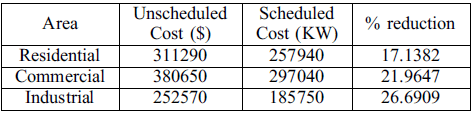
schedule their maximum load where the price is low, that leads to reduced electricity bill as shown in Fig. 4. It is clear from the Fig. 4 that residential users minimize their daily electricity bill by proper load scheduling. Residential area reduce their electricity bill from 311290$ to 257940$ per day, which results in about 17.1382% reduction in daily electricity bill. Moreover, the residential area reduces its peak load from 1886 KW to 1489 KW which results in about 21.04% reduction in peak load. Residential area have a large number of controllable appliances. Results show that the residential load has efficiently manage in response to the RTP signal. Generally, by increase in number of controllable loads the DSM results are better, but the complexity of the problem is increasing. In DSM, cost saving depends upon the customer inconvenience, more the customer wait more the saving. In residential area tolerance level of shifting the load in a far away slot is high for most appliances. It signifies that the residential customers do not have stringent predilection regarding time of operation of controllable load as compared to commercial or industrial loads. Results from the commercial area are shown in Fig. 5. Commercial users schedule their load where the price is low, that leads to reduced electricity bill as shown in Fig. 6. It is clear from the Fig. 6 that Commercial users minimize their daily electricity bill by proper load scheduling. The commercial area reduce their electricity bill from 380650$
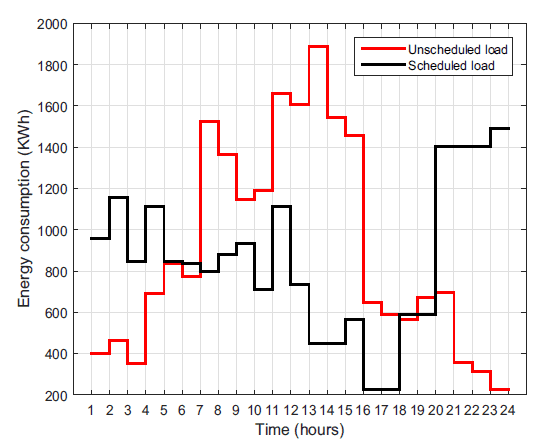
Fig. 3. Residential area daily energy consumption

Fig. 4. Residential area daily electricity bill
to 297040 $ per day, which results in about 21.9647% reduction in daily electricity bill. Moreover, the commercial area reduces its peak load from 2301 KW to 1752 KW which results in about 23.85% reduction in peak load. It is clear from results that commercial area has less number of controllable loads than the residential area, but cost reduction in the commercial area is more than a residential area. This is due to the energy consumption of the loads. Scheduling of large energy consumption load results in more saving.
Fig. 7 shows the results from the industrial area. Industrial users modify their energy consumption profile in response to an RTP signal to minimize their monetary expense as well as reduce their PAR. This leads to reduced electricity bill as shown in Fig. 8. It is clear from the Fig. 8 that industrial area, minimize their daily electricity bill by proper load scheduling. Industrial area reduce their electricity bill from 252570$ to
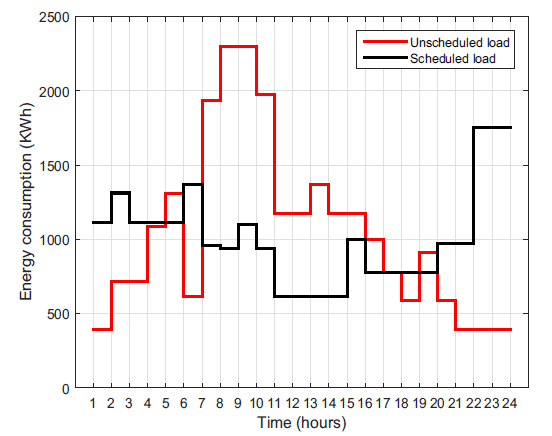
Fig. 5. Commercial area daily energy consumption

Fig. 6. Commercial area daily electricity bill
185750 $ per day, which results in about 26.6909% reduction in daily electricity bill. Moreover, the industrial area reduces its peak load from 1863 KW to 1388 KW which results in about 25.49% reduction in peak load. It is clear from the results that industrial users have less number of controllable loads as compared to residential and commercial area, but cost reduction in industrial area is more than residential and commercial area. Moreover, scheduling the large energy consumption loads results in better PAR reduction as well as cost reduction.
In an efficient DSM, benefits are not only for customers, but also for utility. One of the key advantage is the reduction in PAR to improve the grid efficiency, stability, capacity and reduce the power generation cost. Spinning reserve capacity is also increased with the decrease in peak load. Overall operational cost and peak demand reduction is shown in table

Fig. 7. Industrial area daily energy consumption

Fig. 8. Industrial area daily electricity bill
5 and 6, respectively.
TABLE V OVERALL COST REDUCTION
VII. CONCLUSION
In this research work, DSM algorithm for various types of controllable appliances of several types is proposed using GA. In this regard, a load scheduling problem is formulated as a cost minimization problem and solved by using GA. Each area minimizes its electricity bill by proper load shifting as well
TABLE VI OVERALL PEAK DEMAND REDUCTION

as reduce its peak load demand by following the constraints. Simulations show that each area efficiently utilizes the grid energy and minimizes its cumulative expense. Moreover, this proposed strategy is beneficial for entire SG, particularly at distribution network level. By reduction in peak load demand the distribution network capacity and reliability is increased. This strategy can be employed in the future SG. Finally, the simulation results show that the proposed algorithm efficiently reduce the PAR and electricity consumption cost.
REFERENCES
- I. K. Maharjan, Demand Side Management: Load Management, Load Proling, Load Shifting, Residential and Industrial Consumer, Energy Audit, Reliability, Urban, Semi–Urban and Rural Setting. Saar–brcken, Germany: LAP (Lambert Acad. Publ.), 2010.
- D. P. Kothari, Modern Power System Analysis. New Delhi, India: Tata McGraw–Hill, 2003.
- C. W. Gellings, Demand–Side Management: Concepts and Methods. Liburn, GA: Fairmont, 1988.
- T. Logenthiran, D. Srinivasan, T. Z. Shun,
Demand Side Management in Smart Grid using Heuristic Optimization
, IEEE Transactions on Smart Grid, vol. 3, no. 3, pp. 1244–1252, 2012. - Z. Zhu, J. Tang, S. Lambotharan, W. H. Chin, Z. Fan,
An integer linear programming based optimization for home demand–side management in smart grid
, In Innovative Smart Grid Technologies (ISGT), IEEE PES, pp. 1–5, January 2012 - C. G. Tomasso, Z. Guchuan, A. F. Miguel, S. Gilles,
A System Architecture for Autonomous Demand Side Load Management in Smart Buildings
, IEEE Transaction on Smart Grid, pp. 2157–2165, vol. 3, no. 4, December 2012. - M. E. Kantarci, H. T. Mouftah.
Wireless Sensor Networks for Cost– Efficient Residential Energy Management in the Smart Grid
, IEEE Transactions on Smart Grid, pp. 314–325, vol. 2, no. 2, 2011. - W. Yuan, K. N. L. Vincent, K. H. Tsang, Q. Li Ping, M. Limin
Optimal Energy Scheduling for Residential Smart Grid with Centralized Renewable Energy Source
, IEEE Systems Journal, pp. 562–576, vol. 8, no. 2, 2014. - A. Alessandro, P. de Gianluca, D. Paolo, V. Antonio,
Load Sceduling for Household Energy Consumption Optimization
, IEEE Transaction on Smart Grid, pp. 2364–2373, vol. 4, no. 4, 2013. - S. Shengan, P. Manisa, R. Saifur.
Demand Response as a Load Shaping Tool in an Intelligent Grid With Electric Vehicles
, IEEE Transactions on Smart Grid, pp. 624–631, vol.2, no.4, 2011. - Y. Peizhong, D. Xihua, I. Abiodun, Z. Chi, L. Shufang.
Real–time Oppertunistic Scheduling for Residential Demand Response
, IEEE Transaction on Smart Grid, pp. 227–234, vol. 4, no. 1, 2013. - Y. Guo, M. Pan, Y. Fang,
Optimal Power Management of Residential Customers in the Smart Grid
, IEEE Transactions on Parallel and Distributed Systems, vol. 23, no. 9, pp. 1593–1606, 2012. - P. Yang, P. Chavali, E. Gilboa, A. Nehorai,
Parallel Load Schedule Optimization with Renewable Distributed Generators in Smart Grids
, IEEE Transactions on Smart Grid, vol. 4, no. 3, pp. 1431–1441, 2013.