ВВЕДЕНИЕ
Физика как естественная наука представляет собой совокупность теоретических и экспериментальных исследований. Теоретическая и экспериментальная составляющие физики развиваются взаимосвязано, взаимно дополняя друг друга. Новые экспериментальные достижения подчас требуют создания новых теорий. И наоборот, достижения в области теоретической физики создают основания для постановки новых экспериментов.
При изучении физики как учебной дисциплины важно получить навыки как экспериментальных, так и теоретических исследований.
Основные навыки экспериментальных исследований в курсе общей физики приобретаются в рамках лабораторного практикума.
Основными методами экспериментальных исследований принято считать наблюдение и эксперимент.
Наблюдение – это систематическое, целенаправленное восприятие того или иного объекта, явления или процесса без воздействия на него. Наблюдение позволяет получить первоначальную информацию об изучаемом объекте, явлении или процессе.
Эксперимент – метод изучения объекта (явления, процесса), при котором исследователь активно и целенаправленно воздействует на него путем создания искусственных условий или использует естественные условия, необходимые для выявления некоторых свойств данного объекта (явления, процесса).
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
Понятие «точность измерения», т.е. степень приближения результатов измерений к некоторому действительному значению, используется для качественного сравнения измерительных операций. Для количественной оценки используется понятие «погрешность измерений». Эти понятия тесно связаны друг с другом: чем меньше погрешность, тем выше точность. Оценка погрешности измерений – одно из важных мероприятий по обеспечению достоверности выполненных измерений.
Количество факторов, влияющих на точность измерений, достаточно велико, и любая классификация погрешностей измерений в известной мере условна. На схеме, изображенной на рис. 1, приведена одна из возможных классификаций, которая может служить основой для оценки погрешности измерений в учебной физической лаборатории. Рассмотрим некоторые из приведенных на схеме видов погрешностей подробнее.
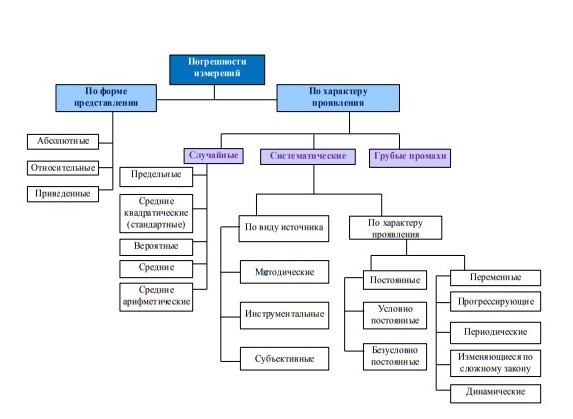
Рис.1. Классификация погрешности измерений
Абсолютная погрешность Δx измерения определяется через разность x0 - x между истинным x0 и измеренным x значениями физической величины. Эта разность может быть положительной или отрицательной в зависимости от того уменьшен или увеличен результат измерения по отношению к истинному значению. Под абсолютной погрешностью, обычно, понимают модуль разности Δx = |x0 – x| между истинным x0 и измеренным x значениями физической величины.
Относительная погрешность δ – отношение абсолютной погрешности Δx к истинному значению x0 или к результату измерения x. Относительная погрешность выражается в долях единицы или в процентах.
Случайные погрешности – это погрешности, при которых величина и (или) знак разности между истинным и измеренным значениями физической величины изменяются от опыта к опыту при измерениях, выполненных одинаковым образом и при одинаковых условиях. Случайные погрешности обуславливаются большим числом случайных причин, действующих в каждом отдельном измерении различным, неизвестным образом. К числу таких причин относятся случайные вибрации отдельных частей прибора, кратковременные случайные изменения в окружающей среде (температурные, оптические, электрические, магнитные воздействия, изменение влажности, колебание воздуха), трение, физиологическое изменение органов чувств экспериментатора (например, утомление) и множество других причин, которые практически невозможно исключить. Предсказать величину случайной погрешности для одного измерения в принципе невозможно. Поэтому приходится повторять измерения до определенного разумного предела, а полученную совокупность экспериментальных результатов обрабатывать с помощью методов теории вероятностей и математической статистики, которые являются основой, так называемой, теории погрешностей.
Литература
1. Кортнев А.В., Рублев Ю.В., Куценко А.Н. Практикум по физике. М.: Издательство «Высшая школа», 1965. 568 с.
2. Кунце Х.-И. Методы физических измерений: Пер. с нем. М:
Мир, 1989. 216 с.
3. Савчук В.П. Обработка результатов измерений. Физическая
лаборатория. Ч. 1. Одесса: ОНПУ, 2002. 54 с.
4. Горбоконенко В.Д., Шикина В.Е. Метрология в вопросах и ответах. Ульяновск: УлГТУ, 2005. 196 с.
5. Сергеев А.Г. Метрология. М: Логос, 2005. 272 с.
6. Корнелл П. Анализ данных в Excell. Просто как дважды два /
П. Корнелл; пер. с англ. М.: Эксмо, 2006. 224 с.
7. Симонович С.В., Евсеев Г.А., Алексеев А.Г. Специальная информатика: Учебное пособие. М.: АСТ-Пресс Книга, 2004. 480 с.
8. Информатика. Базовый курс / Симонович С.В. и др. СПб: Издательство «Питер», 2000. 640 с.