Модельное прогнозируемое управление оптимальной зарядкой литий-ионной батареи в режиме реального времени
Real-time Model Predictive Control for the Optimal Charging of a Lithium-ion Battery
1M. Torchio и L. Magni работают в Dipartimento di Ingegneria Civile e Architettura, а D. M. Raimondo работает в Dipartimento di Ingegneria Industriale e dell'Informazione Павийский университет, 27100 Павия, Италия marcello.torchio01@ateneopv.it,{lalo.magni,davide.raimondo}@unipv.it
2N. A. Wolff и U. Krewer работают в Institute of Energy and Process Systems Engineering, Брауншвейгский технический университет, ул. Ференца Листа 35, 38106 Брауншвейг, Германия u.krewer@tu-braunschweig.de
4R. B. Gopaluni работает в University of British Columbia, 2360 Восточный Мэлл, Ванкувер, Британская Колумбия, Канада V6T 1Z3 bhushan.gopaluni@ubc.ca
5J. A. Paulson и R. D. Braatz работают в Massachusetts Institute of Technology, Кембридж, штат Массачусетс, Соединенные Штаты Америки 02142 {jpaulson, braatz}@mit.edu
I. Введение
Литий-ионные батареи используются в широком спектре приложений благодаря высокой плотности заряда, высокой объемной и гравиметрической плотности энергии, а также высокому напряжению элементов [1]. Для обеспечения высокой эффективности и предотвращения возможных повреждений литий-ионных батарей требуются усовершенствованные системы управления батареями (ABMs). Промышленные ABMs для литий-ионных батарей зависят от простых эмпирических моделей (например, см. [2], [3], [4]); хотя существуют более совершенные модели (например, см. [5], [6], [7], [8]), их применение в ABMs ограничено из-за стоимости вычислений. Состояние заряда (SOC) – это важное свойство литий-ионных батарей, которое оценивается современными системами управления батареями. SOC определяет количество заряда, оставшегося в батарее, и определяется как интеграл отношения мгновенной концентрации лития на электроде к максимальной концентрации насыщения на соответствующем электроде по времени [9]. Знание SOC может быть использовано для предотвращения повреждения, обеспечения безопасности, уменьшения старения и минимизации времени зарядки. Учитывая, что единственными доступными измерениями для литий-ионной батареи являются напряжение, ток и температура, необходимо оценить SOC. В [10] была разработана модель эквивалентной схемы для оценки SOC, в которой используются резисторы, источники напряжения, конденсаторы и таблицы поиска. Адаптивный расширенный фильтр Калмана для оценки SOC, основанный на улучшенной модели Тевенина, был разработан в [11]. Оценка SOC на основе электрохимической модели одиночных частиц (SPM) обсуждалась в [12] и [13]. Чтобы уменьшить сложность электрохимических моделей, были разработаны математические переформулировки первопринципных моделей батарей с гораздо меньшими вычислительными затратами [14]. Переформулированные модели были использованы для прогнозирования внутренних состояний батареи без снижения точности [15]. Кроме того, в [16] используется подход фильтрации Калмана для оценки SOC в условиях циклического движения на низкой околоземной орбите (LEO). В [17] была предложена стратегия оптимального управления на основе SPM, которая обеспечивает минимальное механическое повреждение частиц электрода в процессе зарядки. Оптимальная стратегия зарядки, направленная на максимизацию запаса энергии батареи, также была предложена на основе переформулированной электрохимической модели первых принципов [18]. В данной статье для точного моделирования поведения батареи используется дискретизированная версия переформулированной электрохимической модели, известная как псевдодвумерная модель пористого электрода (P2D) [7]. Целью данной работы является разработка оптимальной стратегии управления, способной минимизировать время зарядки литий-ионной батареи при соблюдении физических ограничений на выходное напряжение, входной ток и температуру батареи. Решение алгоритмов управления на основе оптимизации в режиме реального времени с использованием сложных моделей, таких как модель P2D, может оказаться непомерно сложным с вычислительной точки зрения. В данной статье проводится аппроксимация динамики вход-выход модели батареи с помощью метода наименьших квадратов. Затем приближенная модель используется в формулировке квадратичного динамического матричного управления (QDMC) [19] для разработки оптимальной стратегии зарядки литий-ионной батареи. Подход QDMC широко используется в промышленных приложениях и может работать с ограничениями на входные и выходные переменные процесса. Мягкие ограничения на выходные переменные и жесткие ограничения на входе включены в формулировку QDMC. Эффективность подхода была проверена на дискретизированной модели P2D в нескольких сценариях. Результаты показывают преимущества предложенного подхода для онлайн-реализации.
II. Модель литий-ионной батареи
A. Псевдодвумерная модель
Этот раздел содержит краткий обзор псевдодвумерной модели, реализованной в [9]. Уравнения модели приведены в таблице I. В процессе зарядки ионы лития транспортируются от анода через сепаратор к катоду. Во время цикла разряда происходит обратный перенос ионов. Модель P2D состоит из связанных между собой дифференциальных уравнений (PDEs) и алгебраических уравнений, которые определяют сохранение массы и заряда в трех секциях – катод, сепаратор, анод – батареи. Индекс \(i \in \begin{Bmatrix} p, s, n \end{Bmatrix}\) используется для обозначения положительного электрода, сепаратора и отрицательного электрода, в то время как \(t \in \mathbb{R}^{+}\) представляет собой индекс времени, \(x \in \mathbb{R}\) обозначает одномерное пространственное направление, вдоль которого перемещаются ионы лития, а \(r(x) \in \mathbb{R}^{+}\) – радиальное расстояние внутри активной частицы в месте \(x\). Концентрация ионов лития в сферических частицах активного материала обозначается \(c_{s}(x, r(x), t) \in \mathbb{R}^{+}\), в то время как средняя концентрация ионов лития в твердых частицах обозначается \(\bar{c_{s}}(x, t) \in \mathbb{R}^{+}\), поверхностная концентрация твердых частиц обозначается \(c_{s}^{*}(x, t) \in \mathbb{R}^{+}\), а концентрация ионов лития в электролите обозначается \(c_{e}(x, t) \in \mathbb{R}^{+}\). Потенциал электролита – \(\Phi_{e}(x, t) \in \mathbb{R}\), потенциал активного материала – \(\Phi_{s}(x, t) \in \mathbb{R}\), а \(\epsilon_{i} \in (0,1)\) и \(D_{i} \in \mathbb{R}^{+}\) – пористость и эффективный коэффициент диффузии на участке \(i\), соответственно. Определим \(a_{i} \in \mathbb{R}^{+}\) как отношение площади поверхности частицы к ее объему, \(t_{+} \in (0,1)\) как число переноса, \(R_{i} \in \mathbb{R}^{+}\) как радиус частицы, \(i_{e}(x,t) \in \mathbb{R}\) как ток в электролите, \(\kappa_{i}(x) \in \mathbb{R}^{+}\) как проводимость электролита, \(R\) как универсальная газовая постоянная, \(T\) как показатель температуры, \(F\) как постоянная Фарадея, \(I(t) \in \mathbb{R}^{+}\) как ток, подаваемый в аккумулятор, \(\sigma_{i} \in \mathbb{R}^{+}\) как эффективная проводимость твердой фазы, и \(j_{i}(x,t) \in \mathbb{R}\) как поток литий-ионов на поверхности твердых частиц. Тепловая модель включает удельную теплоемкость \(C_{p,i}\), соответствующие плотности электродов \(\rho_{i}\) и теплопроводности \(\lambda_{i}\), а также теплопроводности анодного и катодного коллекторов, \(\lambda_{cc}\) и \(\lambda_{ca}\). Наконец, \(l_{i}\) определяет длину каждой секции батареи. Более подробное описание модели можно найти в [7], [9], [20]. Различные параметры модели, используемые в данной статье, взяты из [20].
ТАБЛИЦА I: Псевдодвумерная модель. Положительный электрод охватывает область от \(x = 0\) до \(x = l_{p}\), сепаратор до \(x = l_{s}\), а отрицательный электрод до \(x = l_{n}\).
| Уравнения сохранения | Ограничительные условия | |||||
| Масса | \[x = 0\] | \[x = l_{cc}\] | \[x = l_{p}\] | \[x = l_{s}\] | \[x = l_{n}\] | \[x = l_{ca}\] |
|---|---|---|---|---|---|---|
| \(\epsilon_{i} \frac{\partial c_{e}}{\partial t} = \frac{\partial}{\partial x}(D_{i}\frac{\partial c_{e}}{\partial x}) + a_{i}(1 - t_{+})j_{i}\)
\(\frac{\partial \bar{c}_{s}}{\partial t} = -3\frac{j_{i}}{R_{i}}\) \(c_{s}^{*} - \bar{c}_{s} = \frac{R_{i}}{D_{s}} \frac{j_{i}}{5}\) |
\[\frac{\partial c_{e}}{\partial x} = 0\] | \[-D_{p}\frac{\partial c_{e}}{\partial x} = -D_{s}\frac{\partial c_{e}}{\partial x}\] | \[-D_{s}\frac{\partial c_{e}}{\partial x} = -D_{n}\frac{\partial c_{e}}{\partial x}\] | \[\frac{\partial c_{e}}{\partial x} = 0\] | ||
| Зарядка | ||||||
| \(i_{e} = -\kappa_{i}\frac{\partial \Phi_{e}}{\partial x} + \frac{2\kappa_{i}RT}{F}(1 - t_{+})\frac{\partial\ ln\ c_{e}}{\partial x}\)
\(\frac{\partial i_{e}}{\partial x} = a_{i}Fj_{i}\) \(\frac{\partial \Phi_{s}}{\partial x} = \frac{i_{e} - I}{\sigma_{i}}\) |
\(\frac{\partial \Phi_{e}}{\partial x} = 0\)
\(i_{e} = 0\) |
\(-\kappa_{p}\frac{\partial \Phi_{e}}{\partial x} = -\kappa_{s}\frac{\partial \Phi_{e}}{\partial x}\)
\(i_{e} = I\) |
\(-\kappa_{s}\frac{\partial \Phi_{e}}{\partial x} = -\kappa_{n}\frac{\partial \Phi_{e}}{\partial x}\)
\(i_{e} = I\) |
\(\frac{\partial \Phi_{e}}{\partial x} = 0\)
\(i_{e} = 0\) |
||
| Температура | ||||||
| \(\rho_{i}C_{p,i}\frac{\partial T}{\partial t} = \frac{\partial}{\partial x}(\lambda_{i}\frac{\partial T}{\partial t}) + Q_{i}\) | \(\frac{\partial T}{\partial t} = 0\) | \(-\lambda_{cc}\frac{\partial T}{\partial x} = -\lambda_{p}\frac{\partial T}{\partial x}\) | \(-\lambda_{p}\frac{\partial T}{\partial x} = -\lambda_{s}\frac{\partial T}{\partial x}\) | \(-\lambda_{s}\frac{\partial T}{\partial x} = -\lambda_{n}\frac{\partial T}{\partial x}\) | \(-\lambda_{n}\frac{\partial T}{\partial x} = -\lambda_{ca}\frac{\partial T}{\partial x}\) | \(\frac{\partial T}{\partial t} = 0\) |
Состояние заряда количественно определяет величину заряда, оставшегося в аккумуляторе. Пусть \(c_{\textup{max}}\) будет максимально возможной концентрацией литий-ионов в твердых частицах в данном электроде, тогда SOC в соответствующем электроде определяется как (в уравнении используется положительный электрод)
| \[ S(t) = \frac{1}{l_{p}}\int_{0}^{l_{p}}\frac{\bar{c_{s}}(x,t)}{c_{\textup{max}}}dx \] | (1) |
Выходное напряжение определяется как
\[ V(t) = \Phi_{s}(0,t) - \Phi_{s}(l_{n},t). \]
Метод дискретизации из [9] используется для определения приблизительной модели шагового отклика, которая используется в контроллере.
B. Идентификация модели шагового отклика
Для того, чтобы получить модель батареи, подходящую для управления на основе оптимизации в режиме онлайн, модель ступенчатого отклика была определена с помощью метода наименьших квадратов (LS).
1) Модели с пошаговым откликом: Учитывая модель ступенчатого отклика динамической системы, выход на дискретном временном шаге \(k\) определяется как
\[ y_{k} = \sum_{i=1}^{N-1}S_{i}\Delta u_{k-i} + S_{N}u_{k-N} \]
- \(S_{i}\) – коэффициенты ступенчатого отклика.
- \(\Delta u_{k} = u_{k} - u_{k-1}\) – разница между двумя соседними входными значениями на временном шаге \(k\).
2) Идентификация LS: Рассмотрим динамическую систему с набором выходов \(ss := \begin{Bmatrix} 1, 2, \cdots, N_{y} \end{Bmatrix}\). Для идентификации модели ступенчатого отклика система подвергается ступенчатым входам величиной \(j \in \jmath\), где \(\jmath\) – конечное подмножество \(\mathbb{R}\). Определим \(\Lambda_{b}^{j} \in \mathbb{R}^{N}\) как вектор столбцов, содержащий данные выходной последовательности \(b\)-го выхода в результате ступенчатого входа величиной \(j\). Для асимптотически устойчивых систем \(N\) представляет собой время установления. Для интегрирующих систем можно сделать эквивалентное предположение, что после \(N\) шагов вся устойчивая динамика затухает, и отклики всех интегрирующих выходов становятся чистыми темпами. Для каждого \(b \in \ss\) определим \(\Lambda_{b} := \begin{bmatrix} (\Lambda_{b}^{j_{1}})^{T}, \cdots, (\Lambda_{b}^{j_{d}})^{T} \end{bmatrix}^{T}\) и затем \(\tilde{\Lambda} := \begin{bmatrix} \Lambda_{1}^{T}, \cdots, \Lambda_{N_{y}}^{T} \end{bmatrix}^{T}\). Коэффициенты ступенчатого отклика \(S\) системы оцениваются решением задачи наименьшего квадрата
\[ S := \textup{arg}\ \underset{\bar{S}}{\textup{min}} \left \| \Phi \bar{S} - \tilde{\Lambda } \right \|_{2}^{2} \]
где
\[ \Phi := I_{N_{y}} \otimes \mathbb{R}^{N_{y}N|\ \jmath\ |\times N_{y}N}, \]
\[ W := \begin{bmatrix} j_{1}I_{N},j_{2}I_{N}, \cdots, j_{d}I_{N} \end{bmatrix}^{T} \in \mathbb{R}^{N|\ \jmath\ |\times N}, \]
оператор \(\otimes\) определяет произведение Кронекера между матрицами, номенклатура \(|\cdot|\) обозначает кардинальность множества, а \(I_{M}\) определяет квадратную матрицу тождества размерности \(M \times M\).
III. Квадратичное динамическое матричное управление (QDMC)
В этом разделе приводится краткий обзор алгоритма QDMC для систем SISO. Этот алгоритм управления использует модель ступенчатого отклика для прогнозирования будущего выхода. Расширение на системы MIMO является простым; более подробную информацию см. в [19], [21], [22].
A. Прогнозы будущих выходов
Определим свободный отклик \(f_{k+i|k}\) как выход системы \(y_{k+i}\) при условии, что изменения управляющей переменной равны нулю от \(k\) в дальнейшем:
\(f_{k+i|k} := y_{k+i}\) в случае, если \(\Delta u_{k+i} = 0, \forall i \geq 0\)
и представить
\[ f_{k} := \begin{bmatrix} f_{k|k}\ f_{k+1|k\ \cdots \ f_{k+N-1|k}} \end{bmatrix}^{T} \in \mathbb{R}^{N} \]
где номенклатура \(x_{i|k}\) представляет значение \(x\) в момент времени \(i\), начиная с момента \(k\). Для асимптотически устойчивых систем ступенчатые отклики приблизительно постоянны после \(N\) шагов времени, т.е. \(f_{k+N|k} \approx f_{k+N+1|k} \approx \cdots \approx f_{k+\infty|k}\). Прогнозируемое значение выхода на один шаг вперед равно \(\hat{y}_{k+1|k} = S_{1}\Delta u_{k|k} + f_{k+1|k}\).
В общем случае прогнозы могут быть сделаны и на \(h\) шагов вперед, причем \(h \geq 0\). Обозначим горизонт прогнозирования через \(h\), а горизонт управления через \(m\), причем \(h \geq m\). Из вычислительных соображений, которые будут объяснены позже, предположим, что входные вариации ограничены нулем, т.е., \(\Delta u_{k+g|k} = 0, \hat{y}_{k+g|k} = f_{k+g|k}\ \forall g = m + 1, \cdots, h.\) Чтобы обобщить формулировку на прогнозирование на \(h\) шагов вперед, введем обозначение
| \[ \hat{y}_{k} = \Psi f_{k} + S_{f}\Delta u_{k} \] | (2) |
где
\[ \hat{y}_{k} := \begin{bmatrix} \hat{y}_{k+1|k}\ \hat{y}_{k+2|k}\ \cdots\ \hat{y}_{k+h|k} \end{bmatrix}^{T} \in \mathbb{R}^{h}, \]
\[ \Delta u_{k} := \begin{bmatrix} \Delta u_{k|k}\ \Delta u_{k+1|k}\ \cdots\ \Delta u_{k+m-1|k} \end{bmatrix}^{T} \in \mathbb{R}^{m}, \]
\(\Psi\) – соответствующая матрица, используемая в качестве сдвигающей маски для массива \(f_{k}\), а матрица \(S_{f}\) содержит коэффициенты ступенчатого отклика
| \[ S_{f} = \begin{bmatrix} S_{1} & 0 & \cdots & 0 \\ S_{2} & S_{1} & \ddots & \vdots \\ \vdots & \vdots & \ddots & 0 \\ \vdots & \vdots & \ddots & S_{1} \\ \vdots & \vdots & \ddots & \vdots \\ S_{h} & S_{h-1} & \cdots & S_{h-m+1} \end{bmatrix} \in \mathbb{R}^{h\times m}. \] | (3) |
В момент времени \(k + 1\) массив свободного отклика \(f_{k+1}\) изменяется следующим образом
| \[ f_{k+1} := \Gamma f_{k} + S\Delta u_{k|k} \] | (4) |
где \(S \in \mathbb{R}^{N}\) – массив, содержащий все коэффициенты ступенчатого отклика, а \(\Gamma \in \mathbb{R}^{N\times N}\) – матрица
| \[ \Gamma := \begin{bmatrix} 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \ddots & \cdots \\ \cdots & \cdots & \ddots & \ddots & 0 \\ 0 & 0 & \cdots & 0 & 1 \\ 0 & 0 & \cdots & 0 & 1 \end{bmatrix} \in \mathbb{R}^{N\times N} \] | (5) |
и \(f_{0} \in \mathbb{R}^{N}\) – начальное значение массива свободного отклика.
Примечание: Эта формулировка \(\Gamma\) подходит для асимптотически устойчивых систем. Когда выход модели показывает интегрирующее поведение, матрица \(\Gamma\) переопределяется как [23]
| \[ \Gamma := \begin{bmatrix} 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & 0 \\ 0 & 0 & \cdots & 0 & 1 \\ 0 & \cdots & 0 & -1 & 2 \end{bmatrix} \in \mathbb{R}^{N\times N} \] | (6) |
В этом случае последний элемент \(f_{k+1}\) определяется как
\[ f_{k+N-1|k+1} := f_{k+N-1|k} + (f_{k+N-1|k} - f_{k+N-2|k}) + S_{N}\Delta u_{k|k} \]
который учитывает интегрирующую тенденцию выходного сигнала. Чтобы учесть несоответствие между моделью ступенчатого отклика и исходной нелинейной системой, необходим поправочный элемент, основанный на фактическом измерении выходного сигнала. Определим \(\omega_{k} := \begin{bmatrix} \omega_{k+1|k}\ \omega_{k+2|k}\ \cdots\ \omega_{k+h|k} \end{bmatrix}^{T} \in \mathbb{R}^{h}\) как массив будущих неопределенностей, действующих на систему. Учитывая, что элементы в \(\omega_{k}\) не могут быть измерены, хорошей оценкой будет \(\omega_{k|k} = y_{k}^{meas} - f_{k|k}\), где \(y_{k}^{meas}\) – измеренный выход в момент времени \(k\). Прогнозирование предполагает, что \(\omega_{k|k} = \omega_{k+1|k} = \cdots = \omega_{k+h|k}.\) Уравнение прогнозирования становится
\[ \hat{y}_{k} = \Psi f_{k} + S_{f}\Delta u_{k} + \omega_{k}, \]
которая содержит в себе долю прошлых входов (\(\Psi f_{k}\)), будущих управляющих воздействий (\(S_{f}\Delta u_{k}\)) и поправочный элемент (\(\omega_{k}\)).
B. Закон оптимального управления
Алгоритм QDMC обеспечивает оптимальную входную последовательность \(\Delta u_{k}\), способную минимизировать функцию затрат \(J(\Delta u_{k})\) при соблюдении ограничений на вход и выход. Задача оптимизации может быть сформулирована следующим образом
\[ \underset{\Delta u_{k}}{\textup{min}}J(\Delta u_{k}) = {e_{k}}^{T}Qe_{k} + \Delta {u_{k}}^{T}R\Delta u_{k} \]
в зависимости от
\[ \begin{matrix} \Delta u_{\textup{min}} \leq \Delta u_{k} \leq \Delta u_{\textup{max}} \\ u_{\textup{min}} \leq u_{k} \leq u_{\textup{max}} \\ \Delta y_{\textup{min}} \leq \Delta\hat{y}_{k} \leq \Delta y_{\textup{max}} \\ y_{\textup{min}} \leq \hat{y}_{k} \leq y_{\textup{max}} \end{matrix} \]
где массив
\[ e_{k} = \Psi f_{k} + S_{f}\Delta u_{k} + \omega_{k} - r \]
представляет собой разницу между прогнозируемыми выходами \(\hat{y}_{k}\) и опорной траекторией \(r\), а матрицы \(Q\) и \(R\) являются соответствующими весовыми коэффициентами для опорного отслеживания и вариаций входного сигнала. Для обеспечения выполнимости задачи оптимизации учитываются мягкие ограничения на выход, при которых закон управления альтернативно выражается как
\[ \underset{\Delta \tilde{u}_{k}}{\textup{min}}\ J = \frac{1}{2}\Delta \tilde{u}_{k}^{T}\tilde{H}\Delta \tilde{u}_{k} + \tilde{c}^{T}\Delta \tilde{u}_{k} \]
в зависимости от
\[ \tilde{A}\Delta \tilde{u}_{k} \leq b \]
где \(\tilde{H}\) и \(\tilde{A}\) – соответствующие матрицы, а \(\Delta \tilde{u}_{k}\), \(\tilde{c}\) и \(b\) – соответствующие векторы, учитывающие наличие мягких ограничений. За более подробной информацией можно обратиться к [24].
C. Подход с уходящим горизонтом
Алгоритм управления QDMC использует так называемый подход с уходящим горизонтом (RH). На каждом временном шаге \(k\) вычисляется оптимальная входная последовательность \(\Delta u_{k}^{\textup{opt}}\); только первая входная вариация применяется к установке, так что управляющее воздействие на временном шаге \(k\) является
\[ u_{k} = u_{k-1} + \Delta u_{k|k}^{opt} \]
где \(u_{k-1}\) – значение входного сигнала, подаваемого на установку в момент времени \(k-1\).
IV. Моделирование
Напряжение и температура предполагаются измеренными, в то время как SOC предполагается как мера, полученная путем оценки, как в (1). Как указано в разделе II-B, модель ступенчатого отклика, используемая для прогнозирования выходного сигнала, была определена с помощью LS. Определим \(\jmath = \begin{Bmatrix} 2, 3, 4, 8, 16 \end{Bmatrix}, N_{y} = \begin{Bmatrix} 1, 2, 3 \end{Bmatrix},\) и для каждого выхода \(N = 185\). На рис. 1-3 показаны идентифицированные модели ступенчатого отклика для трех измеренных переменных (напряжение, SOC и температура). Эти выходы показывают интегрирующее поведение, что приводит к реализации QDMC с использованием матрицы \(\Gamma\), определенной в (6). Моделирование проводилось по различным сценариям, которые имеют общие ограничения:
\[ \begin{matrix} -3\times 10^{-3}\ \textup{V} \leq \Delta V_{\textup{out}} \leq 3\times 10^{-3}\ \textup{V} \\ 2.6\ \textup{V} \leq V_{\textup{out}} \leq 4.2\ \textup{V} \\ 0 \leq I_{\textup{in}} \leq 2C \\ -15\frac{\textup{A}}{\textup{m}^{2}} \leq \Delta I_{\textup{in}} \leq 15\frac{\textup{A}}{\textup{m}^{2}} \\ 0.45 \leq SOC_{\textup{out}} \leq 0.95 \end{matrix} \]
со скоростью \(C 29.5\ \textup{A}/\textup{m}^{2}\). Управляемая переменная SOC будет отслеживаться до заданного значения. Начальное значение SOC равно 49% (для имитации наполовину разряженной батареи), а целевое значение установлено равным 85%. Первоначально батарея поддерживается в устойчивом состоянии путем снижения тока до нуля и ожидания стабилизации температуры. \(T_{\textup{ref}}\) – это атмосферная температура, при которой работает батарея; \(Q_{SOC} = 10I_{h}\) для каждого сценария, а значение \(R\) варьируется. Горизонт управления \(m\) и горизонт прогнозирования \(h\) были выбраны равными 80 шагам, с временем выборки \(T_{s} = 0.5\ \textup{с}\), что соответствует пропускной способности системы. Моделирование проводилось с использованием MATLAB и оптимизационного решателя TOMLAB [25] для моделирования P2D модели и MOSEK [26] для алгоритма оптимального управления на 64-битной процессорной системе i5 @ 3.2-GHz с 8 Гб оперативной памяти и ОС Ubuntu 14.04. Процессорное время, необходимое MOSEK для решения задачи оптимизации, составляет около \(0.1\ \textup{с}\). Переменные \(\gamma_{i}\) описывают вес нарушения мягких ограничений. Параметры контроллера для различных сценариев определяются (где не указано, \(\gamma_{\Delta V} = \gamma_{SOC} = \gamma_{V} = \gamma_{Temp} = 10^{3}\))
| \[T_{\textup{out}}\] | \[T_{\textup{ref}}\] | \[\gamma_{V}\] | \[R\] | |
| Сценарий 1: | \[\leq 313.5\ \textup{K}\] | \[\leq 298.15\ \textup{K}\] | \[10^{3}\] | \[0.1, 1, 10\] |
| Сценарий 2: | \[\leq +\infty\ \textup{K}\] | \[\leq 298.15\ \textup{K}\] | \[10^{2}\] | \[1\] |
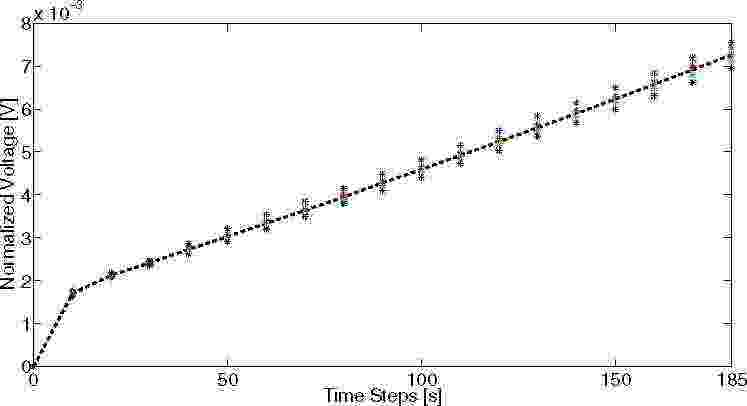
Рис. 1.: Модель ступенчатого отклика напряжения: расчетная модель входа-выхода LS (пунктирная черная линия) и выходные значения, полученные при различных ступенчатых входах (звездочки).
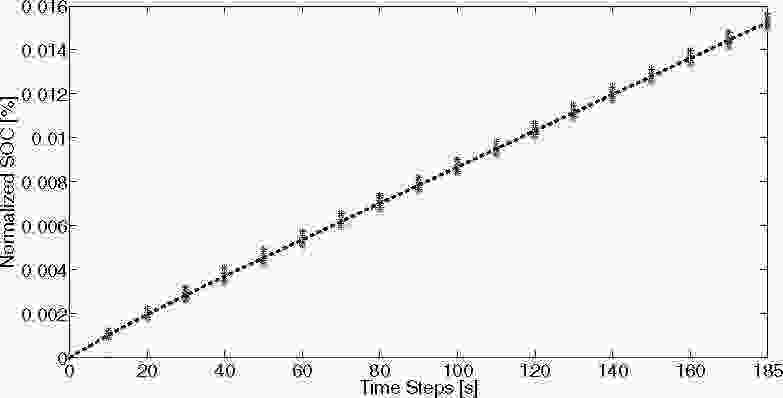
Рис. 2.: Модель ступенчатого отклика в состоянии заряда: расчетная модель входа-выхода LS (пунктирная черная линия) и выходные значения, полученные при различных ступенчатых входах (звездочки).
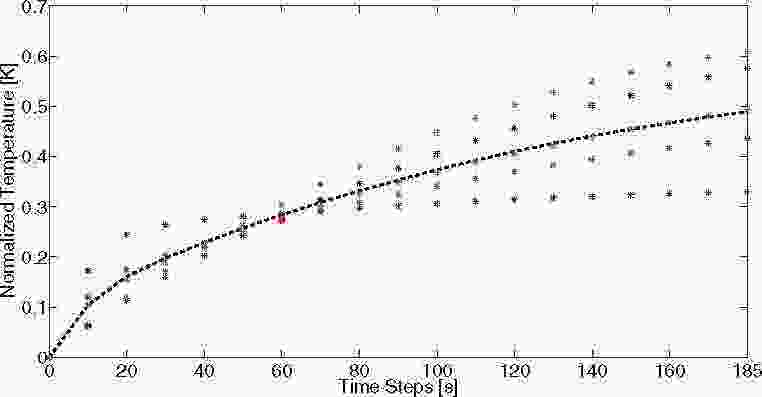
Рис. 3.: Модель ступенчатого отклика температуры: расчетная модель входа-выхода LS (пунктирная черная линия) и выходные значения, полученные при различных ступенчатых входах (звездочки).
A. Результаты сценария 1
Сценарий 1 оценивает влияние \(R\) на управляющее воздействие (см. рис. 4а). Значения \(R = 0.1\) и \(1\) имеют схожую тенденцию, в то время как менее агрессивное \(R = 10\) демонстрирует задержку управляющего воздействия. Профили SOC на рис. 4b показывают, что заданное значение 85% достигается примерно через \(1700\ \textup{с}\) для всех значений \(R\), при этом \(R = 10\) дает большее значение SOC около \(500\ \textup{с}\), а затем меньшее значение около \(1000\ \textup{с}\). Оба ограничения по напряжению удовлетворяются в течение всего времени для \(R = 1\) и \(10\) (рис. 4c), с небольшим нарушением верхней границы при \(1500\ \textup{с}\) для \(R = 0.1\), при этом напряжение приближается к \(4.1\ \textup{В}\) в более длительное время для всех значений \(R\). Ограничение по температуре немного нарушается около \(500\ \textup{с}\) для каждого значения \(R\) (рис. 4d), что допускается смягчением ограничения. Нарушение может быть уменьшено или устранено путем более сильного взвешивания мягкого ограничения или путем смещения верхней границы температуры в алгоритме вниз на небольшую величину.
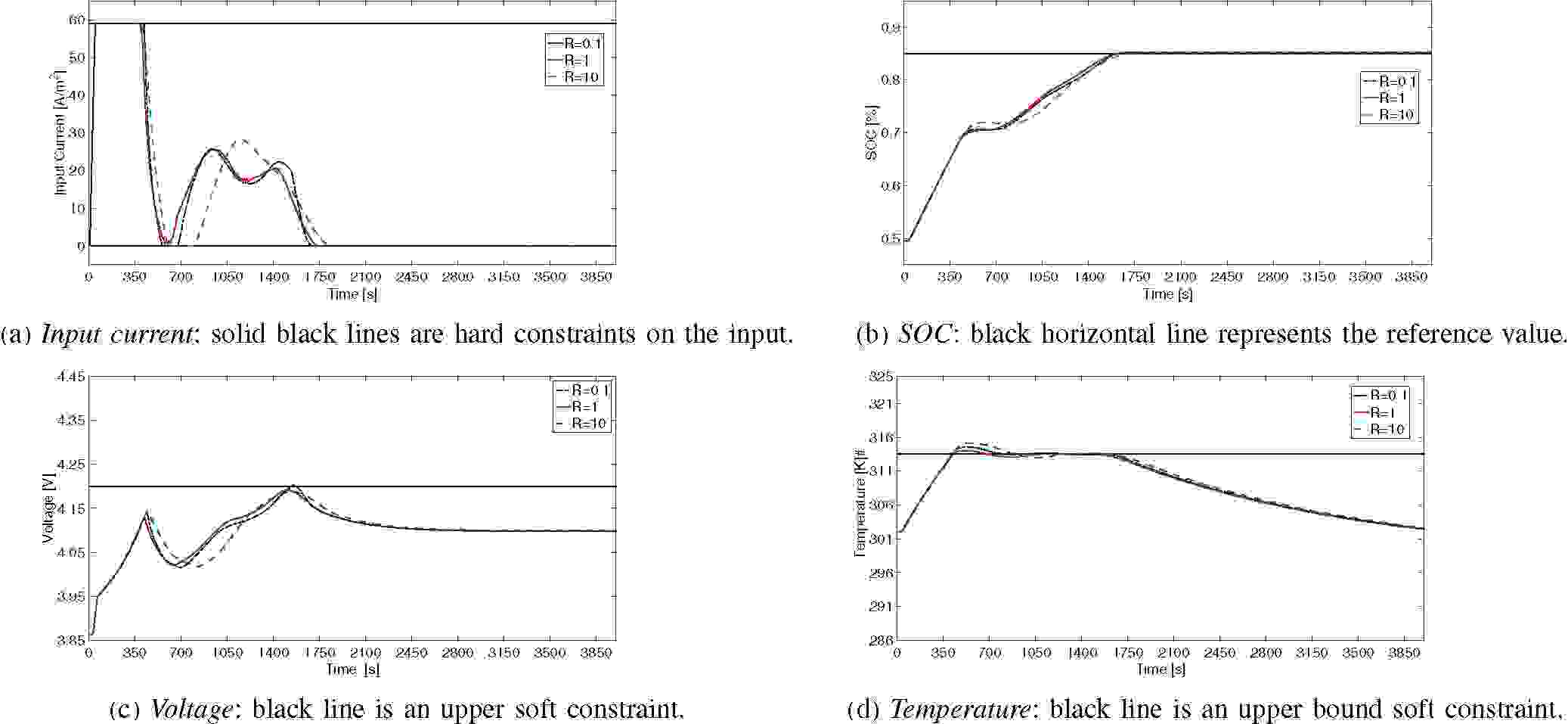
Рис. 4.: Результаты сценария 1
B. Результаты сценария 2
Чтобы сократить время зарядки батареи, в этом сценарии ослабляется ограничение верхней границы температуры и множитель нарушения напряжения \(\gamma_{V}\). Как и ожидалось, напряжение и температура превышают свои гипотетические верхние границы (см. рис. 5c и 5d), примерно на \(10\ \textup{K}\) и \(0.08\ \textup{В}\), соответственно. В отличие от сценария 1 (рис. 4a), инжектируемый ток для сценария 2 на рис. 5a не падает почти до нуля за \(600\ \textup{с}\), чтобы перестроиться для выполнения температурных ограничений. Снятие ограничений приводит к тому, что входной ток почти сразу достигает своего максимально допустимого значения в течение всего процесса зарядки и падает только тогда, когда SOC приближается к конечному установленному значению. Эти графики показывают высокую важность включения температурных ограничений при оптимальной зарядке батарей. SOC в сценарии 2 достигает контрольного значения 85% примерно за \(1200\ \textup{с}\) (рис. 5b), что почти на десять минут меньше, чем в сценарии 1. Величина наклона SOC почти постоянна в течение всего процесса зарядки, что позволяет достичь заданного значения раньше.
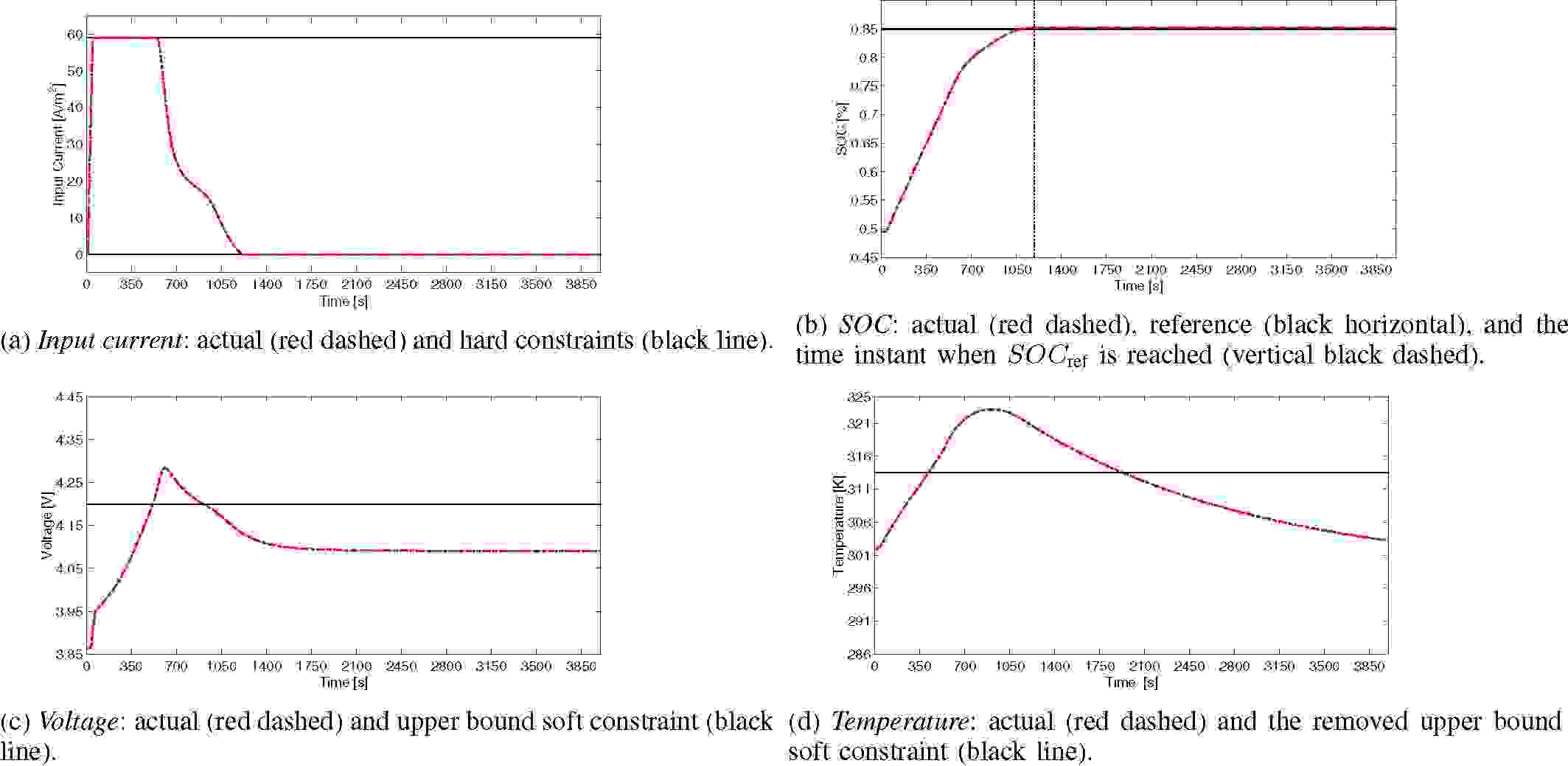
Рис. 5.: Результаты сценария 2
Благодарность
R. D. Braatz выражает благодарность за финансовую поддержку от Edwin R. Gilliland Professorship. R. B. Gopaluni выражает благодарность за финансовую поддержку от Natural Sciences and Engineering Research Council of Canada.
Заключение
Модель литий-ионной батареи P2D – это электрохимическая модель на основе PDE, способная связать динамику батареи с физическими ограничениями, но слишком сложная для реализации в режиме реального времени для большинства алгоритмов оптимального управления. В данной работе разработана аппроксимация модели P2D и включена в квадратичный динамический матричный контроллер для минимизации времени зарядки батареи. Алгоритм управления учитывает ограничения по току, SOC и температуре батареи. Алгоритм управления разработан таким образом, чтобы смягчить ограничения для улучшения производительности. Моделирование показывает пригодность данного подхода для применения в режиме реального времени.
Ссылки
- C. Daniel, "Materials and processing for lithium-ion batteries", JOM, vol. 60, no. 9, pp. 43-48, 2008.
- M. Chen and G. A. Rincon-Mora, "Accurate electrical battery model capable of predicting runtime and IV performance", IEEE Transactions on Energy Conversion, vol. 21, no. 2, pp. 504-511, 2006.
- B. Yann Liaw, G. Nagasubramanian, R. G. Jungst, and D. H. Doughty, "Modeling of lithium ion cells – A simple equivalent-circuit model approach", Solid State Ionics, vol. 175, no. 1, pp. 835-839, 2004.
С полным перечнем ссылок можно ознакомиться в оригинале статьи.