УДК 621.355: 519.713
Оценка остаточной емкости литий-ионного аккумулятора на основе эталонной модели
1ОАО Научно-производственный центр
Полюс
Россия, 634050, г. Томск, просп. Кирова, 56в. E-mail: m.khandorin@gmail.com
2Национальный исследовательский Томский политехнический университет
Россия, 634050, г. Томск, просп. Ленина, 30. E-mail: bukreev@tpu.ru
Предлагается способ подстройки интегрирующего счетчика ампер-часов аккумулятора на основе эмпирической модели, характеризующей его состояние. Приведены результаты моделирования в среде Matlab Simulink.
Ключевые слова: литий-ионный аккумулятор, интегрирующий счетчик ампер-часов, модель Тевенина, сплайн-интерполяция.
Evaluation of lithium-ion battery discharge capacity based on the reference model
1JSC Research and production center
Polyus
56v, Kirov prosp., Tomsk, 634050, Russia. E-mail: m.khandorin@gmail.com
2National Research Tomsk Polytechnic University
30, Lenin prosp., Tomsk, 634050, Russia. E-mail: bukreev@tpu.ru
Propoused a method of buttery integrating amper-houer counter adjustment based on the empirical model. Shows the results of mathematical modeling in Matlab Simulink environment.
Keywords: lithium-ion battery, integrating ampere-hour counter, Thevenin model, spline-interpolation.
При эксплуатации космических аппаратов большое значение имеет оценка остаточной емкости аккумуляторной батареи системы электропитания. Для широко применяемых в настоящее время литий-ионных аккумуляторов задачу оценки остаточной емкости можно решить при помощи счетчика ампер-часов. При этом счетчик устанавливается на максимальное значение при полном заряде батареи, и по мере ее разряда значение емкости будет уменьшаться пропорционально израсходованной энергии. Этот метод достаточно адекватно работает, если каждый заряд будет проводиться до достижения максимальной емкости. Однако чередование режимов заряда и разряда батареи без достижения ее полного заряда и накопление ошибки в счетчике ампер-часов вследствие различных потерь энергии при передаче из зарядного устройства в батарею и из батареи в нагрузку с течением времени приведет к невозможности адекватной оценки остаточной емкости.
Для компенсации ошибок, накопленных в счетчике ампер-часов, введем поправочный коэффициент \(\delta_{i}\):
| \[ C_{ост} = C_{0} - \sum_{i=0}^{n} (I_{i}\Delta t_{i} + \delta_{i}), \] | (1) |
где \(C_{ост}\) – остаточная емкость аккумуляторной батареи, А·ч; \(C_{0}\) – разрядная емкость батареи после полного заряда, А·ч; \(I_{i}\) – ток разряда или заряда на i-м интервале времени; \(\Delta t_{i}\) – длительность i-го интервала времени интегрирования.
Одним из вариантов вычисления коэффициента \(\delta_{i}\) может быть использование эталонной модели изменения напряжения аккумуляторной батареи:
| \[ \delta_{i} = k(U_{и} - U_{м}), \] | (2) |
где \(k\) – нормирующий множитель, способ определения которого рассмотрен ниже; \(U_{и}\) – измеренное значение напряжения аккумуляторной батареи; \(U_{м}\) – значение напряжения аккумуляторной батареи, вычисленное по эталонной модели.
Исходя из обзора эмпирических моделей литийионных аккумуляторных батарей [1; 2], остановимся на модели Тевенина, так как она при относительной простоте реализации учитывает динамические параметры аккумулятора.
Модель выходного напряжения \(U_{м}\) аккумуляторной батареи при заданном значении остаточной емкости \(C_{ост}\) выглядит следующим образом:
| \[ \left\{\begin{matrix} \frac{dU_{Th}}{dt_{i}} = -\frac{U_{Th}}{R_{Th}C_{Th}} + \frac{I_{i}}{C_{Th}}; \\ U_{м} = U_{ос} - U_{Th} - I_{i}R_{0}, \end{matrix}\right. \] | (3) |
где \(U_{Th}\) – падение напряжения, зависящее от химических процессов в аккумуляторе, В; \(R_{Th}\) – эквивалентное сопротивление поляризации аккумулятора, Ом; \(C_{Th}\) – эквивалентная емкость (определяется динамическими параметрами аккумулятора), Ф; \(U_{ос}\) – напряжение разомкнутой цепи аккумулятора, В; \(R_{0}\) – постоянное сопротивление, связанное с конструкцией аккумулятора, Ом.
При этом значения параметров \(R_{Th}\), \(C_{Th}\), \(U_{ос}\) являются функциями от остаточной емкости аккумулятора и могут быть определены экспериментально в любой точке разрядной характеристики [1]. Точки на графике разрядной характеристики, в которых определены параметры, будем называть опорными. На каждом интервале между двумя опорными точками \(\begin{bmatrix}C_{ост_{i-1}}, C_{ост_{i}}\end{bmatrix}\) будем вычислять значения переменных путем интерполяции при помощи кубического сплайна по формулам [3]:
| \[ \left\{\begin{matrix} C{_{Th_{i}}} (C_{ост}) = a{_{c_{i}}} + b{_{c_{i}}} (C_{ост} - C{_{ост_{i}}}) + \\ + \frac{c{_{c_{i}}}}{2} (C_{ост} - C{_{ост_{i}}})^{2} + \frac{d{_{c_{i}}}}{6} (C_{ост} - C{_{ост_{i}}})^{3}; \\ R{_{Th_{i}}} (C_{ост}) = a{_{R_{i}}} + b{_{R_{i}}} (C_{ост} - C{_{ост_{i}}}) + \\ + \frac{c{_{R_{i}}}}{2} (C_{ост} - C{_{ост_{i}}})^{2} + \frac{d{_{R_{i}}}}{6} (C_{ост} - C{_{ост_{i}}})^{3}; \\ U{_{ос_{i}}} (C_{ост}) = a{_{U_{i}}} + b{_{U_{i}}} (C_{ост} - C{_{ост_{i}}}) + \\ + \frac{c{_{U_{i}}}}{2} (C_{ост} - C{_{ост_{i}}})^{2} + \frac{d{_{U_{i}}}}{6} (C_{ост} - C{_{ост_{i}}})^{3}; \end{matrix}\right. \] | (4) |
где \(a\), \(b\), \(c\), \(d\) – коэффициенты сплайна.
Таким образом, получаем семейство сплайнов для описания зависимостей \(R_{Th}\), \(C_{Th}\), \(U_{ос}\) от значений остаточной емкости \(C_{ост}\).
Так как начальный и конечный участки разрядной характеристики c экспоненциальной зависимостью параметров модели от остаточной емкости занимают около 20 % емкости батареи [4], то для обеспечения адекватности модели параметры \(U_{ос}\), \(R_{Th}\), \(C_{Th}\) определяются не менее чем в 20 опорных точках. Достаточно большое количество точек позволит также использовать равномерную сетку при расчете коэффициентов сплайна, что существенно упрощает алгоритм расчета [3].
Следует отметить, что значения параметров \(R_{Th}\), \(C_{Th}\) модели для заряда и разряда аккумулятора будут отличаться при известном значении \(C_{ост}\), поэтому для их описания потребуется, как минимум, два семейства сплайнов.
В качестве имитационной модели реального аккумулятора используется стандартная модель аккумулятора в среде моделирования Simulink, параметры которой соответствуют литий-ионному аккумулятору ЛИГП-10 (ОАО Риггель
).
Параметры эталонной модели Тевенина для подстройки счетчика амперчасов определены для того же аккумулятора.
Нормировочный коэффициент \(k\) определяется экспериментально и находится в пределах 0,0001...0,001. Этот диапазон позволяет производить подстройку модели за приемлемое время и уменьшает перерегулирование.
Для сравнения в модель включены три счетчика ампер-часов: один с подстройкой по эталонной модели Тевенина, другой – без такой подстройки и образцовый, связаный со встроенной моделью. Показания счетчиков с подстройкой по эталонной модели и без подстройки были смещены на 3 А·ч (35 % для данного аккумулятора) для имитации накопленной ошибки. В процессе моделирования попеременного заряда и разряда аккумулятора (изменения тока от 5 А на разряде до 2 А на заряде) выполнялась оценка остаточной емкости аккумулятора (см. рисунок).
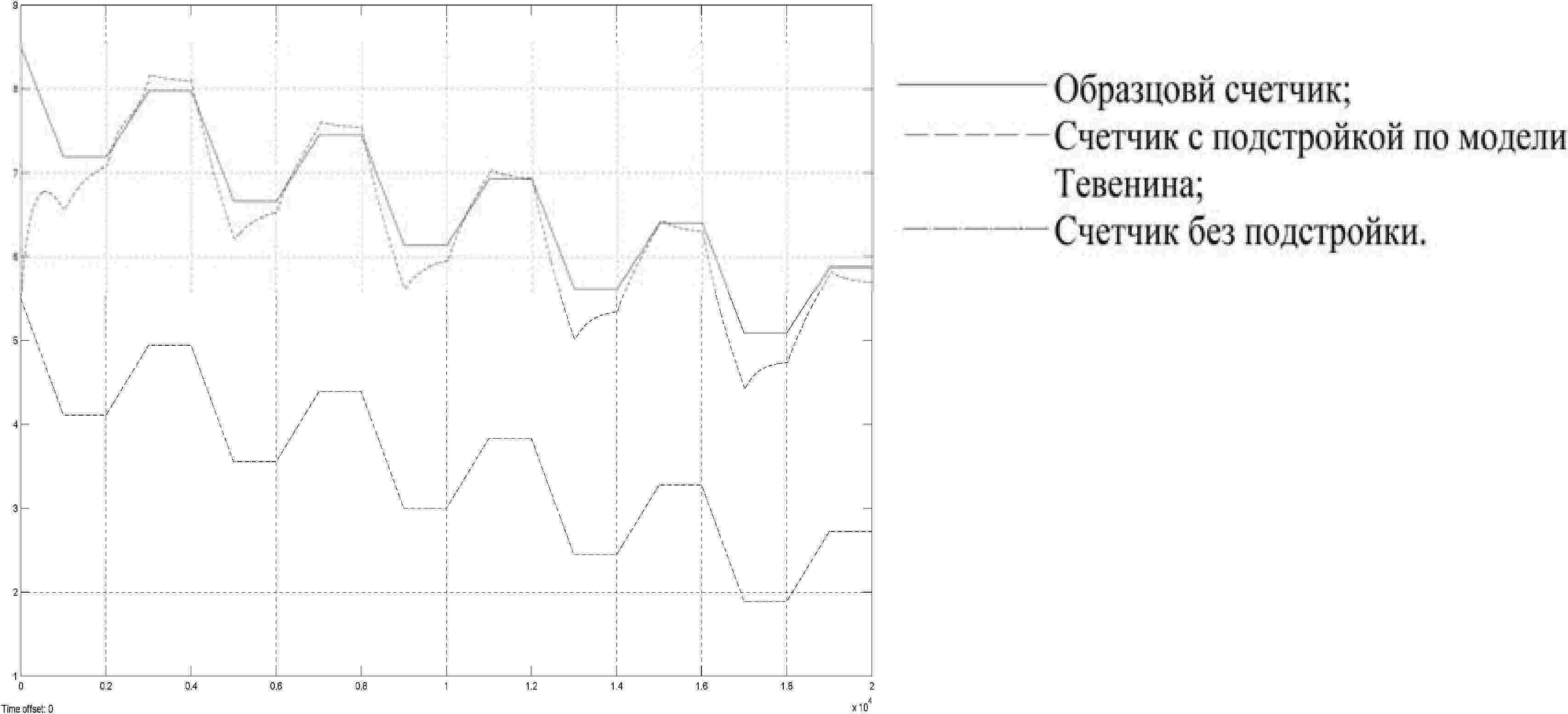
Сравнение работы трех счетчиков ампер-часов
Рассмотренный способ подстройки счетчика ампер-часов позволяет вычислить значение остаточной емкости литий-ионной аккумуляторной батареи в процессе эксплуатации без ее заряда до максимальной емкости и не требует существенных программных ресурсов.
Библиографические ссылки
- Hongwen H., Rui X., Jinxin F. Evaluation of Lithium-Ion Battery Equivalent Circuit Models for State of Charge Estimation by an Experimental Approach // Energies. 2011. № 4. P. 582-598.
- Rahmoun A., Biechl H. Modelling of Li-ion batteries using equivalent circuit diagrams // Przegląd elektrotechniczny (Electrical Review). 2012. № 7b. P. 152-156.
- Роджерс Д., Адамс Дж. Математические основы машинной графики. М. : Мир, 2001.
- Таганова А. А. Герметичные химические источники тока. Элементы и аккумуляторы, оборудование для испытаний и эксплуатации. СПб. : Химиздат, 2005.
References
- Hongwen H., Rui X., Jinxin F. Evaluation of Lithium-Ion Battery Equivalent Circuit Models for State of Charge Estimation by an Experimental Approach // Energies. 2011. № 4. P. 582-598.
- Rahmoun A., Biechl H. Modelling of Li-ion batteries using equivalent circuit diagrams // Przegląd elektrotechniczny (Electrical Review). 2012. № 7b. P. 152-156.
- Rodzhers D., Adams Dzh. Matematicheskie osnovy mashinnoj grafiki. M. : Mir, 2001
- Taganova A. A. Germetichnye himicheskie istochniki toka. Jelementy i akkumuljatory, oborudovanie dlja ispytanij i jekspluatacii. SPb. : Himizdat, 2005.