Аннотация
В статье дана классификация оценок качества изображений. Возможны два подхода к оценке качества изображений: количественная оценка с помощью использования математических методов и субъективная оценка на основе экспертных оценок. С другой стороны, субъективные и количественные оценки качества изображений могут быть абсолютными или сравнительными. В статье представлены наиболее распространенные оценки качества изображения, дана их классификация. Приведены рейтинговые шкалы для субъективной оценки качества изображений.
Введение
Качество цифрового изображения зависит от условий освещения, а также от характеристик регистрирующей системы: соотношения сигнал/шум, статистических характеристик шума, градационных характеристик, интервалов дискретизации спектральных (цветовых) характеристик и т.д. Оценка качества изображения является достаточно сложной комплексной задачей.
1. Классификация оценок качества изображений
Возможны два подхода к оценке качества изображений: количественная оценка с помощью использования математических методов (среднеквадратическая ошибка, Lp-норма [1], меры, учитывающие особенности восприятия изображения зрительной системой человека) и субъективная оценка на основе экспертных оценок.
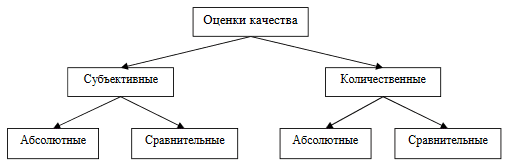
Рисунок 1 — Классификация оценок качества изображения
С другой стороны, субъективные и количественные оценки качества изображений могут быть абсолютными или сравнительными. Абсолютная мера качества используется для оценки одного изображения, т.е. изображению присваивается соответствующая категория в рейтинговой шкале. Сравнительные меры используются для ранжирования набора изображений в качественной шкале от «лучше всего» до «хуже всего» или взаимного сравнения двух изображений, например, исходного и отфильтрованного (или полученного в разные дни, разными камерами и т.д.). На рис. 1 представлена классификация оценок качества изображений. Подробнее оценки рассматриваются в следующих разделах.
2. Субъективные оценки качества изображений
Субъективная оценка качества изображения зависит от различных внешних факторов, например, условий окружающей среды, освещения, настроения специалиста, который производит оценку, качества монитора, характера рассматриваемых изображе—ний и др. Существует два вида экспертных оценок: абсолютные и сравнительные [5].
В табл. 1 приведены примеры рейтинговых шкал, использованных для субъективной оценки качества изображений [4], [6].
Таблица 1 — Рейтинговые шкалы для субъективной оценки качества изображений

Зрительная система человека — наиболее надежный и совершенный измерительный инструмент, оценивающий качество цифрового изображения. Однако субъективная оценка — это довольно затруднительный и медленный процесс, который требует опытных экспертов и не является объективным и универсальным.
Для решения задачи оценки качества изображения в общем виде нужно найти количественные оценки, которые наилучшим образом соответствуют субъективным. Такие оценки можно получить в несколько этапов:
- подготавливается представительный набор изображений, на котором выполняются оценки качества;
- осуществляется количественный анализ качества изображения различными методами, в результате чего получают оценки качества изображения для каждого метода оценивания;
- выполняется субъективный анализ принятого изображения наблюдателями-экспертами, которым демонстрируются изображения. Оценки разных экспертов для одного и того же изображения усредняются;
- сравниваются оценки изображений, полученные количественными и субъективными методами и выясняется, какой из количественных методов наиболее точно характеризует качество изображения.
Для того чтобы количественные оценки качества изображения лучше соответствовали субъективным, следует учитывать особенности человеческого восприятия изображения, например [7]:
- цветовое разрешение человеческого зрения ниже яркостного;
- человек маловосприимчив к мелким цветным деталям.
3. Количественные оценки качества изображений
Количественные меры качества изображения также, как и субъективные, можно разделить на две группы: абсолютные и сравнительные. Абсолютная мера представляет собой число, сопоставляемое любому изображению на основе анализа этого изображения. Сравнительная мера является числовым результатом сравнения двух или более изображений [3]. Для сравнения также можно использовать абсолютные меры, вычисленные для каждого изображения по отдельности.
3.1. Абсолютные оценки
3.1.1. Оценка резкости изображения
Резкость изображения — один из важнейших показателей его качества, во многом определяющий пригодность изображения к дальнейшей обработке. Резкость изображения — это степень размытости границы между двумя соседними участками изображения с разной оптической плотностью (яркостью). На рис. 2а) представлено резкое изображение, на рис. 2б) — тоже изображение, но размытое. Авторы [8] предлагают определять меру резкости изображения S путем нахождения угла наклона профиля яркости изображения на границе перепада (рис. 2д)).

где i — количество краевых пикселей на изображении, w — это ширина перепада, G — это разница между значениями яркостей пикселей, обозначенных a и b (рис. 2д)).
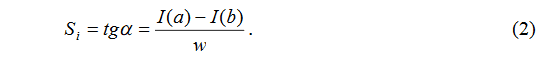
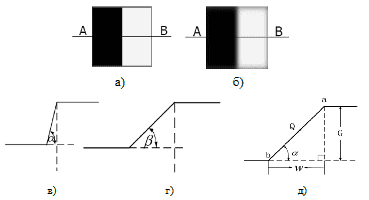
Рисунок 2 — а) исходное изображение; б) размытое изображение; в), г) профили яркостей изображений а) и б); д) схема вычисления угла наклона
Предложенный алгоритм включает следующие шаги.
- 1. Выделить краевые пиксели, используя детектор краев.
- 2. В цикле, для каждого краевого пикселя, определить направление градиента.
- 3. В цикле, для каждого краевого пикселя, вдоль направления градиента найти ближайшие пиксели с минимальным
a и максимальным b значениями яркостей и расстояние между ними w (рис. 2д)).
- 4. Вычислить меру резкости для каждого краевого пикселя Si, подставив w, a и b в (2).
- 5. Максимальное значение из всех полученных является мерой резкости изображения S: S = max{Si}.

Рисунок 3 — Изображения, размытые усредняющим фильтром радиуса R и их количественная оценка резкости S
Примеры вычисления предложенной оценки резкости изображений представлены на рис. 3 — 4. Использовалось 2 типа размытия исходных изображений: усреднение (по окружности радиуса R) и размытие в горизонтальном направлении на D пикселей. В экспериментах использовались полутоновые изображения. Для оценки резкости цветных изображений они преобразуются в одно из цветовых пространств YСbСr, HSV, HSL и мера S вычисляется только для компоненты яркости.

Рисунок 4 — Изображения с разной степенью горизонтального размытия на D пикселей и их количественная оценка резкости S
3.1.2. Оценка контраста изображения
Еще одним параметром, который определяет качество изображений, является контраст. Контраст — это градационная характеристика черно-белого или цветного изображения по различию в светлоте (насыщенности цвета) его наиболее ярких и наиболее темных участков.
Поскольку изображение имеет сложный сюжетный характер, то это порождает необходимость при определении его контрастности выходить из контраста отдельных комбинаций элементов изображения [9]. При этом все элементы считаются равнозначными, и контраст каждой их пары вычисляется по формуле (3). Пиксели для сравнения можно выбирать различными способами. Наиболее простой способ — сравнение соседних пикселей в горизонтальном и вертикальном направлении.

где Li , Lj — яркости элементов изображения. Далее, применяя правило суммирования контрастов, вычисляют набор величин, которые определяют восприятие каждой пары элементов изображения. Проводя усреднение матрицы локальных контрастов, получают суммарный контраст. Полученный результат может быть использован как один из параметров оценки визуального качества изображения.
Существует еще один метод оценки качества изображения. Его суть состоит в следующем. Экспериментально было установлено, что оптимальное, с точки зрения субъективного восприятия, изображение имеет нормальное распределение яркостей его элементов. Для удобства дальнейших расчетов был применен критерий нормального распределения. По степени отклонения реального распределения яркостей от нормального проводилась оценка качества изображения. Кроме количественной оценки качества изображения, данный метод позволяет получить информацию о на- личии и весовом соотношении яркостных градаций изображения. Результаты оценки качества изображения, полученные по данному методу, хорошо коррелируют с субъективной оценкой визуального качества изображения [9].
Если в (1) вместо G подставить (3), получится комбинированная оценка резкости и яркости изображения.
Определение абсолютной количественной оценки качества изображения — это очень сложная, трудоемкая и до сих пор не решенная до конца задача. На практике чаще всего используют сравнительные количественные меры качества изображений.
3.2. Сравнительные оценки двух изображений
3.2.1. Среднеквадратическая ошибка, пиковое отношение сигнал-шум
Наиболее часто используемые сравнительные оценки качества двух изображений — это среднеквадратическая ошибка (СКО) и пиковое отношение сигнал-шум (ПСКО). Методы, основанные на этих оценках, хороши для изображений, имеющих белый шум. Однако эти меры некорректно отражают структурные искажения при кодировании (сжатии) изображения, а также плохо коррелируют с визуальной оценкой качества [10]. На рис. 5 приведены примеры изображений и их значения среднеквадратической ошибки и пикового отношения сигнала/шум.

Рисунок 5 — Оценка качества изображения «Эйнштейн» с разным типом шума а) исходное изображение; б) искаженное изображение: СКО = 14,5, ПСКО = 24,9 dB; в) искаженное изображение: СКО = 15,5, ПСКО = 24,3 dB. Оба искаженных изображения имеют приблизительно одинаковые значения среднеквадратической ошибки и пикового отношения сигнала/шум
Уайлдер [11] провел глубокое исследование свойств абсолютной и среднеквадратической ошибок в дискретной форме применительно к степенному, логарифмическому и градиентному преобразованиям, а также к преобразованию Лапласа. Было выяснено, что поэлементные преобразования в сочетании с критериями абсолютной и среднеквадратической ошибок не позволяют получить меру качества изображения, согласующегося с субъективными оценками.
3.2.2. Оценка резкости изображений
Одной из количественных сравнительных оценок качества изображения может служить резкость. В предложенном
алгоритме резкость измерялась путем вычисления меры эксцесса двумерного спектра Фурье.
Алгоритм определения резкости изображения
- 1. Выделить прямоугольную область на изображении.
- 2. Выделенную область интереса преобразовать в частотную область.
- 3. Вычислить меру эксцесса двумерного спектра Фурье полученной области.
Эксцесс определяется как отношение четвертого центрального момента и квадрата второго центрального момента (стандартное отклонение в четвертой степени) (4).

где μ2 — второй центральный момент, μ4 — четвертый центральный момент, σ — стандартное отклонение.
- Конец алгоритма.
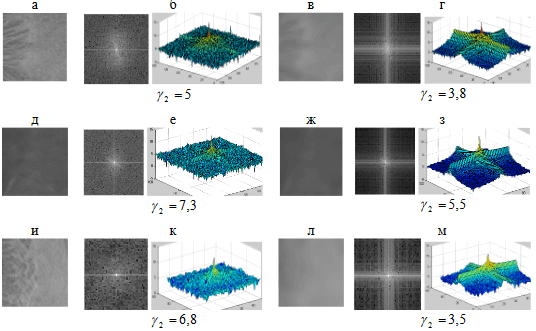
Рисунок 6 — а, д, и — исходные изображения областей РОГ (100x100 пикселей); б, е, к — Фурье спектры исходных изображений; в, ж, л — Размытое изображение (ф.Гаусса R=10, σ=25); г, з, м — Фурье спектр размытого изображения
В экспериментах использовались изображения радужной оболочки глаза (РОГ). Были вырезаны прямоугольные области (100x100 пикселей). Сравнивались мера эксцесса спектра Фурье исходного изображения и мера эксцесса спектра Фурье изображения, обработанного фильтром Гаусса. Результаты оценки резкости изображений РОГ приведены на рис. 6.
Так как высоких пространственных частот на резком изображении больше, чем на размытом, следовательно, двумерное распределение спектра Фурье для резкого изображения будет шире. Более резкому изображению радужки соответствует большая величина эксцесса.
3.2.3. Норма Минковского
Эта мера оценивает разницу между двумя изображениями X = {xij} и Y = {yij}.

где Lp — значение нормы Минковского. Значение при сравнении идентичных изображений равно нулю [12]. Норма Минковского не учитывает структурного подобия изображений. Пример приведен на рис. 7, где два тестовых сигнала сгенерированы из исходного изображения. Структурная информация исходного изображения практически полностью потеряна во втором тестовом примере, но сохранена в первом. Чтобы вычислить норму Минковского, сначала вычитаем исходный сигнал из тестовых сигналов, получая ошибочные сигналы 1 и 2, у которых совсем разная структура. Однако применение абсолютного оператора к полученным результатам дает одинаковую абсолютную ошибку. И, как следствие, одинаковые значения норм Минковского, даже при различных значениях параметра p. Пример демонстрирует, что норма Минковского не всегда соответствует визуальной оценке сходства изображений, имеющих одинаковое значение нормы. А также показывает, что структурная информация изображения играет важную роль в методах оценки качества изображений.

Рисунок 7 — Одинаковые нормы Минковского для разных пар изображений
3.2.4. Мера структурного подобия
Мера структурного подобия была предложена Вангом в работе [13] для сравнения полутоновых изображений. Значение меры структурного подобия вычисляется по формулам:
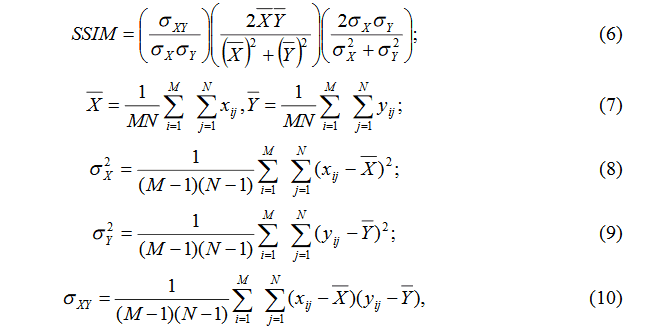
где SSIM — значение меры сходства (качества) изображений; X = {xij} и Y = {yij} — сравниваемые изображения; M, N — размеры изображения. Первая составляющая выражения (6) является коэффициентом корреляции между изображениями X и Y. Вторая составляющая характеризует сходство средних значений яркостей двух сравниваемых изображений. Третья составляющая характеризует сходство контрастов двух сравниваемых изображений.

Рисунок 8 — Оценка качества изображений при помощи меры структурного подобия SSIM: а) — исходное изображение со спутника 285x185 пикселей; б) — изображение, обработанное фильтром Гаусса с параметрами: σ = 5, R = 15; в) — изображение, обработанное фильтром Гаусса с параметрами: σ = 15, R = 30
Чем выше значение меры сходства изображений, тем лучше выполнена обработка изображения. В общем случае мера сходства изображений рассчитывается в непересекающихся областях для каждого изображения отдельно. Поскольку на изображениях сцены объекты не изменялись и не двигались, меру можно вычислять сразу на всем изображении. Результаты экспериментов представлены на рис. 8 — 9.

Рисунок 9 — Сравнения качества изображений при помощи меры структурного подобия SSIM: а) — исходное изображение со спутника 500x500 пикселей; б) — изображение, обработанное фильтром Кувахара с маской 3х3; в) — изображение, обработанное фильтром Кувахара с маской 5х5
Заключение
Очевидно, что количественные меры качества изображения необходимы для проектирования и оценки систем воспроизведения изображений. Эти меры во многом помогут избавиться от трудоемкой и неточной современной методики оценки изображений посредством субъективной экспертизы. Кроме того, на основе количественных мер можно развивать методы оптимизации систем обработки изображений.
В разработке количественных оценок качества изображения достигнуты значительные успехи. Однако введенные критерии не являются достаточно совершенными. Большинство попыток найти приемлемые оценки качества изображения относится к частным случаям. Предлагается некая оценка, основанная на каких-либо физиологических предпосылках, а чаще просто удобная для анализа и вычислений, а затем оцениваются его свойства. Создание более совершенных оценок качества изображений связано с более глубоким изучением свойств зрительной системы человека.
Перечень источников
- Jain A.K. Fundamentals of Digital Image Processing. — Prentice-Hall, Inc., USA, 1989.
- Limb J.O. Distortion Criteria of the Human Viewer. IEEE Transactions on Systems // Man and Cybernetics. —
December 1979. — Vol. 9, № 12. — Р. 778-793.
- Pratt W.K. Digital Image Processing. — John Wiley and Sons, Inc., USA, 1978.
- Snyder H.L. Image quality: Measures and visual performance // Flat-Panel Displays and CRTs. — Tannas L.E.,
Jr. Ed. — New York: Van Nostrand Reinhold, 1985. — Р. 70-90.
- Shnayderman A., Gusev A., Eskicioglu A.M. An SVD-Based Gray-Scale Image Quality Measure for Local and Global
Assessment // IEEE Transactionson image processing. — February 2006. — Vol. 15, №. 2.
- Netravali A.N. and Limb J.O. Picture Coding: A Review // Proceedings of the IEEE. — March 1980. — Vol. 68, №
3. — Р. 366-406.
- Гугель Ю.В., Гуров В.С., Гуров И.П., Семенов Н.В., Шалаев М.А. Оценка качества передачи динамических
изображений в формате mpeg по реальным каналам связи // VII Всероссийская научно-методическая конференция
«Телематика'2000».
- Wang X., Tian B., Liang C., Shi D. Blind Image Quality Assessment for Measuring Image Blur // Congress on
Image and Signal 2008 Congress on Image and Signal Processing, 2008.
- Журавель И.М. Краткий курс теории обработки изображений.
- Avcibas I., Sankur B., Sayood K. Statistical evaluating of image quality measures // Journal of Electronic
Imaging. — April 2002. — Vol.11, № 2. — Р. 206-223.
- Wilder W.C. Subjective Relevant Error Criteria for Pictorial Data Processing // Purdue University, School of
Electrical Engineering, Report TR-EE 72-34, December 1972.
- Макаров А.О. Алгоритмы увеличения пространственного разрешения и обработки мультиспектральных спутниковых
изображений: Дис… к-та техн. наук: 05.13.01/ А.О. Макаров. — Минск, 2006. — 156 с.
- Wang Z., Bovik A.C., Sheikh H.R. Image quality assessment: From error visibility to structural similarity // IEEE transaction on Image Processing. — 2004. — Vol. 13, № 4. — P. 309-12.