Abstract
Attention! At the time of this writing, the master's work has not yet been completed. Estimated completion date – May 2022. The full text of the work, as well as materials on the topic, can be obtained from the author or his supervisor after that date.
Content
- Introduction
- 1. Theme urgency
- 2. Goal and tasks of the research
- 3. Basic laws (principles) of quantum mechanics
- 4. Born-Oppenheimer approximation
- 5. Jahn-Teller theorem
- 6. Self-consistent field approximation
- References
Introduction
In problems related to structure, geometry, vibrational and electronic spectra of molecules, research methods based on the laws of classical physics are not applicable. For nano and smaller systems, quantum theory, quantum mechanics [1] was developed in the first third of the 20th century. Its main equation, the Schrödinger equation, is exactly solved for one- and two-particle systems, taking into account their interaction. There are no such solutions even for three partial systems.
For many-particle systems, approximate methods for solving the Schrödinger equation were developed,
based on
the use of a test wave function of a certain form with minimization of the value of the energy functional
with respect to free
parameters for each approximate wave function. In this case, the quantum
theory of the atom took into account its spherical symmetry both for each atomic orbital and for the
many-particle wave function of the atom by using the Clebsch-Gordan coefficients for both its spatial and
spin parts. And the requirement of a certain orbital and spin moments of the many-partial state led to the
allowance for the interaction of a limited number of electronic configurations. In the quantum theory of
molecules, the Hartree-Fock methods are widely used, unlimited or limited in spin, based on a test wave
function in the form of a determinant of spin-orbitals.
1. Theme urgency
It should be noted that the problem of matching the spatial symmetry of a molecule for a wave function with a certain spatial and spin symmetry is taken into account by introducing a limited configurational interaction, and averaging of degenerate molecular states in a number of cases allows, moreover, the preservation of the matrix form of writing the energy functional, as was assumed without exact proof in [13]. The electron energy functional for such approximate, test, wave functions is constructed at a fixed position of the nuclei, reflecting the symmetry of the molecule, and then minimized.
The application of the variational principle to this functional, when the variable quantities are molecular orbitals, gives the equations for their calculation. The peculiarity of these equations is in their nonlinearity.
In a model sense, an electron in a molecular orbital determined from these equations is in the averaged field created by electrons in the same, so far unknown, molecular orbitals.
The method for solving such equations is iterative. Its result naturally depends on the geometry of the initial approximation for the molecular orbital. In the presence of the degeneracy of the MO at the threshold of the instability developed in the invariant matrix formulation by M. M. Mestechkin, new solutions may appear. As a solution to the equation of instability, they can arise according to different principles. This is either a branch of a known solution with the same symmetry, or the emergence of a new, possibly asymmetric, solution.
The degenerate electronic states are characterized by the presence of the Yann-Teller effect. Nevertheless,
configuration instability is physically induced not by the actual degeneracy of electronic states, but
rather not by the symmetric distribution of charges on an arbitrary degenerate state
. For the linear
Schrödinger equation, the wave function belongs to the irreducible representation of the point group of
the
molecule, that is, it agrees with the symmetry of the nuclear core. The situation is different for nonlinear
Hartree-Fock equations. Here, spontaneous symmetry breaking at the threshold of instability is of interest
for explaining the physical nature of the Yann-Teller effect for molecules in the Hartree-Fock
approximation.
2. Goal and tasks of the research
The task of this work is to find additional solutions with reduced symmetry for the instability equations. In this case, the priority task is to search for such situations when the emerging instabilities are universal, that is, appearing in an initially symmetric molecular system. The search for such solutions will be carried out in the MO LCAO-approximation in the restricted Hartree-Fock method for systems with a symmetry axis of the third order. It is assumed that such systems have universal instability with violation of the indicated symmetry, which will allow us to discuss the limits of its applicability.
One of the additional tasks is the qualitative visualization of the results obtained by drawings of energy surfaces determined by the perturbation theory at the threshold of the nascent asymmetric solution. The presence of the nucleation of asymmetric solutions with lower energies will also change the symmetry of the potential for nuclei, which will lead to a change in the spatial symmetry of the molecule itself.
3. Basic laws (principles) of quantum mechanics
At the end of the 19th century, a number of experimental facts accumulated: Kirchhoff's law for thermal radiation of an absolutely black body, the laws of the photoelectric effect, line spectra of atoms and molecules, the absence of a difference in the speed of light along the direction of motion of the Earth and across it. And none of them could be explained within the framework of classical mechanics and electrodynamics, well developed by that time.
The first steps towards the creation of a quantum theory were Planck's hypothesis about the quantization of radiation and Louis-de-Broglie's hypothesis about the wave properties of matter. The work of Born, Schrödinger, Heisenberg, and Dirac completed the creation of a mathematical model of quantum mechanics in the 1920s. It is based on a number of postulates, principles that cannot be derived or substantiated theoretically. [1-3].
Dualism of Louis de Broglie, wave-particle
, fundamentally distinguishes a microparticle, a
nano-particle, from the particles we are used to and from the waves we are used to. For a nanoparticle, the
concept of a trajectory loses its meaning, since motion along a trajectory is incompatible with the
phenomenon of diffraction and interference inherent in it. But now all the principles (laws) of quantum
mechanics (its mathematical model) are fully experimentally confirmed.
In quantum mechanics (QM), the motion of a free particle with momentum p in vacuum is associated with a plane monochromatic wave, the function:
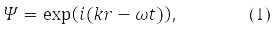
where, according to de Broglie's hypothesis
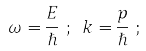
E – particle energy, ℏ = 1,05*10-34J·s – Planck's constant and |p| = 2π/α, α – de Broglie wavelength.
In the general case, instead of (1), the wave function is written
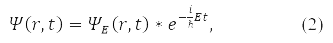
For the wave function (2) in 1926, Max Born proposed a probabilistic interpretation, according to which |ψ(r, t)|2 determines the probability density for a particle to be detected at the moment time t in the vicinity of point r
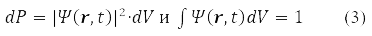
Postulate (3) is generalized to an arbitrary number of particles in the system. Experience has shown that elementary particles have spin and ψ(r,σ,t)include spin variables, σ=α when the spin projection on the OZ axis is 1/2 and σ=β when the projection is -1/2. It is argued that the wave function contains the maximum attainable volume of information about the system, which can be obtained about it in the QM. Moreover, the Pauli principle [1-4] requires that for particles with half-integer spin their wave function be antisymmetric with respect to the permutation of all coordinates of any pair of such particles.
Figure 1 – Molecule rotation
(animation: 7 frames, 5 repetition cycles, 138
kilobytes)
The second principle of quantum mechanics (QM) – this is the principle of superposition. According to it, a system that can be in states with wave functions (WF) ψ1,ψ2,…,ψk, may be in a state
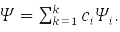
According to the third principle of QM, each observable quantity is associated with a linear Hermitian operator, for example:
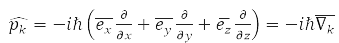
– momentum operator of the k-th particle
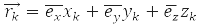
– coordinate operator of the k-th particle, operator of its energy:
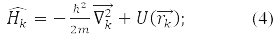
According to the fourth principle, the permissible values that can be obtained by measuring the physical quantity A are the eigenvalues of the linear Hermitian operator of this quantity. For example, in a state ψE(rk), corresponding to its own meaning E Hamilton operator:
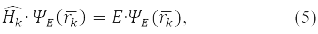
observed energy of the k-th particle Е.
In formulas (4) and (5), the 5th postulate, the principle, QM is also taken into account: the operator of any physical quantity that has a classical analogue can be found by the formulas of classical physics, if in them the coordinates are replaced with momenta by the operators corresponding to them.
A consequence of the 4th and 5th postulates is the statement that two physical quantities can be measured simultaneously (with arbitrarily high accuracy) if and only if their operators commute. Then these operators have the same eigenfunctions.
From the fact that the same projections commute the radius of the vector of the particle and its momentum, [x,px]=[y,py]=[z,pz]=0, следует, что соответствующие проекции не simultaneously measurable, that is, the more accurately one of them is measured, the more uncertain the second of them becomes.
Heisenberg wrote this result in the form of an uncertainty relation:
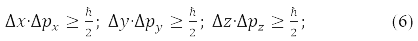
It reflects the fact that microparticles (nanoparticles) lack trajectories.
All projections of the angular momentum operator do not commute with each other, but each of them commutes with the squared angular momentum operator. Therefore, you can simultaneously measure only the square of the angular momentum and one (any) of its projection.
The sixth principle of QM answers the question: How to find the wave function of the state of a
quantum-mechanical system, for which the wave properties of matter are essential?
The answer to this question was given in 1926 by E. Schrödinger. He wrote down the equation that the wave function satisfies
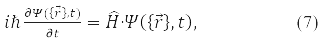
where
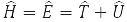
– system energy operator (Hamiltonian operator), T – kinetic energy operator and U – operator of the potential energy of its particles. Formula (5) is written for the wave function of a particle in a stationary (time independent) state. Equation (7) is called the Schrödinger equation.
4. Born-Oppenheimer approximation
All information about a quantum mechanical system is contained in the solution of equation (7). When solving it, the maximum number of commuting operators of physical quantities describing the state of the system is taken into account, including the Hamilton operator, so that the wave function is eigenvalue for them and for the resulting state all these quantities, including energy, are measurable, arbitrarily accurately.
Equation (7) is exactly solved for a particle in a potential field [1, 3]and for two interacting particles. The task for them is simplified by passing to the coordinates of the center of mass and the relative distance r between the particles:
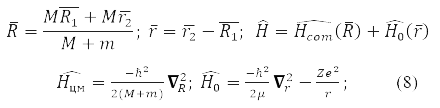
where
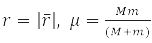
– reduced mass of interacting particles.
In these coordinates, problem (7) is factorized
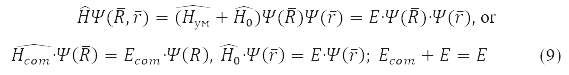
Solution
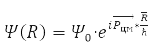
describes the free motion of the center of mass.
Relative Radius Problem
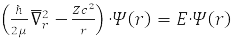
has spherical symmetry and is solved by separating variables in spherical coordinates when choosing a system of commuting operators: the projection of the angular momentum onto the axis OZ, LZ, square of angular momentum L2, and energy H0. For the hydrogen atom М – proton mass and m – electron,
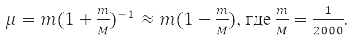
That is, with an accuracy of 0.05%, we can assume that μ=m and the electron moves in the field of a stationary nucleus [1-4].
Для трёхчастичной задачи уже нет точного решения, а есть численные решения уравнения Фадеева [5], в основном для задачи трёхчастного рассеяния с обобщениями на рассеяние большего числа частиц.
Поэтому многочастичная задача решается приближенно. Для атомов и молекул приближённое разделение движения электронов и ядер основывается на указанном выше соотношении их масс,
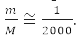
Approximate methods have also been developed for the multielectron problem solved in this case in the field of atomic nuclei of a molecule: from configuration interaction to various self-consistent field methods based on the application of the variational method [4].
For the first time, the separation of electronic and nuclear motions was carried out in the work of Born and Oppenheimer [6].
If we ignore the translational movement of the molecule as a whole, then, in the order of their values, we can distinguish three types of movement – the motion of electrons in the field of nuclei, vibrations of nuclei relative to the center of mass of a molecule, which move slowly compared to electrons in their averaged field, and rotations of a molecule around the axes, coming through the center of mass. Wherein, Eэл.мол ≫ Eэл.мол ≫ Eэл.мол, and the total energy of the molecule: E = Eel. + Ecol. + Er. In this approximation ψ = ψel. + ψcol. + ψr.. Each fixed position of the nuclei corresponds to a certain energy Eэл.({R}). In this sense, electron energy, as a function of internuclear distances, plays the role of potential energy for the nuclei themselves. For stable polyatomic molecules, a simple criterion for the applicability of the Born-Oppenheimer approximations is obtained:
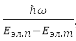
where ω – the highest of the cyclic frequencies of normal vibrations of nuclei near equilibrium points, Eel.p и Eel.t – energies of neighboring electronic states.
5. Jahn-Teller theorem
In 1937, Jan and Teller proved a theorem limiting the possible configurations for atomic nuclei in nonlinear molecular systems. Its proof is based on perturbation theory for degenerate electronic states of a symmetric molecule relative to the displacements of the atoms of the molecule during its normal vibrations, classified according to the irreducible representations of the symmetry group of the molecule. For all molecules, except for linear ones, its proof is based on the presence in the expansion of the square of the irreducible representation of its degenerate electronic state of any irreducible representation possible for the normal vibrations of the molecule (see pp. 209-226 in [7]).
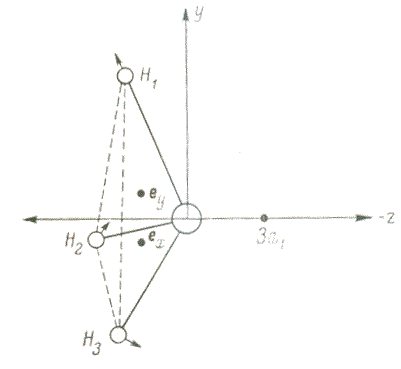
Figure 2 — Jahn-Teller shifts in a molecule BH3
In 1959, Clinton and Rice, relying on the Gelman-Feynman theorem, gave a new justification for the
Jahn-Teller theorem, the physical essence of which is related to the force effect of the charge of the
electron cloud
in the main degenerate ratio of the molecule (determined by their density) on the
nucleus of each atom. On the example of molecules of symmetry D3h и D4h
they showed the possibility of stabilizing asymmetric geometry for them, which can be caused by vibrations
of nuclei with symmetry B1g и B2g (see pp. 379-389 in [7]).
It should be noted that the linear Schrödinger equation with a symmetric arrangement of the nuclei of
the
molecule has a solution belonging to the irreducible representation of the symmetry group of such a
molecule. If its ground electronic state is degenerate, then when one of the state components is realized,
its electron density turns out to be non-symmetric and the strength of their Coulomb interaction with
slow nuclei
, in the cases indicated by Jahn and Teller, can lead to a decrease in the symmetry of
the molecule. Due to the linearity of equation (7), this will also affect its solution for the wave function
of electrons, the symmetry of which will also decrease and, as a result, the degeneracy of the ground state
will be lifted.
6. Self-consistent field approximation
The wave function for the multielectron problem is determined from the solution of the Schrödinger equation (7) in the Born-Oppenheimer approximation with fixed nuclei. Spin interactions are usually taken into account according to perturbation theory.
The impossibility of an exact solution to Eq. (7) led to the development of approximate methods based on minimizing the mean value of the Hamiltonian calculated for a certain test function. When it is presented in the form of an expansion in determinants of spinorbitals taken from a certain basis, we have the method of configurational interaction (QM) [8,9]. The requirement for antisymmetry of the wave function, as mentioned above, follows from the Pauli principle. The KV methods based on the basis of the eigenfunctions of the one-electron Hamiltonian make it possible to classify energy levels, but are not practically convenient for calculations.
The Hartree-Fock self-consistent field method is more efficient. Hartree's method did not take into account the Pauli principle. And Fock corrected it by writing down the determinants of them instead of the product of the orbitals. The equations obtained from the variational principle for molecular orbitals of such a function are essentially nonlinear. An orbital record was also obtained for them [1-4] and matrix form [10]. Вin the latter case, the energy functional in spin-orbital form [11] written like this:
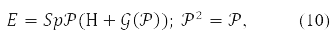
where any of the matrices P,H,𝒢(P), in (9) is decomposable in Pauli matrices acting in the spin space
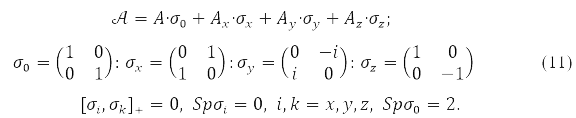
Functional (9), as special cases, includes: and the approximation of different orbitals for different spins (ROSC), the so-called unrestricted Hartree-Fock method (HFR), and the approximation with two-fold filling of the closed shell orbitals – limited Hartree-Fock method (HHF). In the HHF method, only the spin projection has a certain value, while in the HHF method both the total electron spin and its projection.
Instead of one-electron density in problems using the 1st and 2nd variation of the energy functional, δE and δ2E, it is convenient to use an involutive matrix:
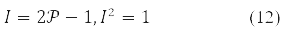
With it, functional (9) takes the form:
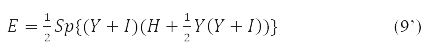
and the stationarity condition
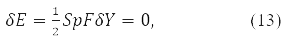
where
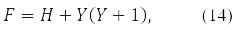
gives the equation:
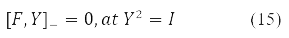
Further energy variation
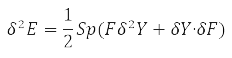
taking into account the properties of the degrees Y-matrix finally gives the value:
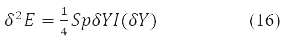
Where δY = D – is the variation matrix of the involutive matrix subject to the condition
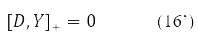
The variation D is transformed in (15) into a new Hermitian matrix I(D) according to the rule [11].
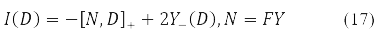
The compact spin-orbit form of the Hartree-Fock equations (14) and the second energy variation (15) - (16) become possible due to the matrix [10] records of both the energy functional, and its 1st and 2nd variations.
When δ2E ≤ 0 we obtain the condition for the instability of the solution of equations (14) for a stationary state. This situation is associated with non-positive eigenvalues of the stability operator (16)
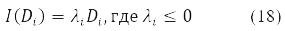
From the form of writing equations (14) - (17), one can extract not only different versions of the Hartree-Fock method, but also consider its instabilities with respect to different types of matrices D, both without spin flip and with spin flip. In work [12], for example, the universal instability of the restricted Hartree-Fock (HHF) method with respect to the variation of the orbitals (and, accordingly, the matrix D) with spin flip for a state with arbitrary total spin is proved.
Various Hartree-Fock methods were obtained under certain requirements for the decomposability (10) of the density Y in Pauli matrices. Thus, the RHF method with a closed shell corresponds to Y = Y0δ0 at Y2 = 1, self-consistent field equations
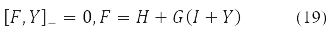
where
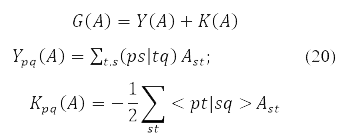
and energy functional
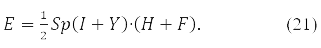
В (19) <qt|qs> – In (19), the integral of 2 partial Coulomb interaction of
electrons
in orbits xp,xt,xq,xs.
References
- Ландау Л.Д. Теоретическая физика. Т. 3: Квантовая механика / Л.Д. Ландау, Е.М. Лифшиц. – 5-е изд. – М.: Физматлит, 2002. – 767 с.
- Мессиа А. Квантовая механика. Т.1 / А. Мессиа. – М.: Наука, 1978. – 478 с.
- Мессиа А. Квантовая механика. Т.2 / А. Мессиа. – М.: Наука, 1979. – 584 с.
- Соколов И.М. Квантовая химия: учеб. пособие / И.М. Соколов. – СПб.: Изд-во Политехн. ун-та, 2010. – 122 с.
- Шмид Э., Цигельман Х. Проблема трёх тел в квантовой механике, монография, перев. с англ. – М.: Наука, 1979, – 272 с.
- Born M., Oppenheimer J.R., Ann. Physik, 1927, V.84, – p. 45
- Нокс Р. и Голд А. Симметрия в твёрдом теле. – М.: Наука, 1970. – 424 с.
- Foresman J. B., Нead-Gordon М., Pople J. A., Frisch М. J. J. Phys. Chem., 1992, v. 96, р. 135.
- Head-Gordon M., Rico R.J., Oumi M., Lee T.J. – Chem. Phys. Jett., 1994, V.219, p. 21
- Местечкин М. М. Метод матрицы плотности в теории молекул. – Киев: «Наукова думка», 1977. – 352 с.
- Местечкин М.М. Нестабильность уравнений Хартри-Фока и устойчивость молекул. – Киев: «Наукова думка», 1986. – 176 с.
- Mestechkin M.M., Klimko G.T., Whyman G.E. On the universal instability of the open-shell Restricted Hartry-Fock method. // Chem. Phys. Lett. – 1985. – V. 115, № 6. – 531 – 534.
- Roothaan C. C. J. Self-Consistent Field Theory for Open Shells of Electronic Systems. – Rev. Mod. Phys., 1960. V. 32, P. 179 – 186.
