Исходные данные для выполнения конструкторскотехнологической подготовки производства цилиндрических колес с пространственно-модифицированными зубчатыми венцами
Автор:Р. М. Грубка, М. В. Долматова, Ю. В. Сазоненко
Источник:Прогрессивные технологии и системы машиностроения № 3 (78)’2022
Аннотация
Р. М. Грубка, М. В. Долматова, Ю. В. Сазоненко Исходные данные для выполнения конструкторскотехнологической подготовки производства цилиндрических колес с пространственно-модифицированными зубчатыми венцами
В статье представлена методика расчета исходных данных для выполнения конструкторскотехнологической подготовки производства цилиндрических колес с пространственномодифицированными зубчатыми венцами. Существующие способы описания боковой поверхности зубьев на этапах выполнения конструкторской и технологической подготовки производства трудоемки,
трудно поддаются автоматизации, которая необходима в современных условиях, особенно при проведении операций с большим количеством данных. Использование предложенной методики позволяет
уменьшить сроки выполнения работ путем описания боковой поверхности пространственномодифицированных зубьев цилиндрических колес семейством сплайнов Безье. В работе представлены основные расчетные зависимости, позволяющие выполнить аппроксимацию координат контактных
точек на боковой поверхности пространственно-модифицированного зуба цилиндрического зубчатого колеса семейством сплайнов Безье третьего порядка, как по высоте, так и по длине зуба.
Ключевые слова:конструкторско-технологическая обеспечение, цилиндрическое колесо, пространственно-модифицированный зубчатый венец, сплайн Безье
1. Введение
Конкурентное машиностроительное производство подразумевает проектирование и применение современных технологий изготовления и сборки деталей машин, использование для изготовления деталей высокотехнологичного и высокопроизводительного оборудования. Назначение и эксплуатационные свойства объекта производства, особенности технологии его изготовления в основном определяют организационную структуру предприятия и характер его производственного цикла. При этом затраты на освоение новых видов продукции непрерывно увеличиваются с усложнением конструкций и необходимостью сокращения сроков освоения производства. Эффективность выпуска изделий определяется совершенством организации производственного процесса с учетом технико-экономических и организационных связей между различными процессами, средствами производства, службами и подразделениями предприя тия. Запуску изготовления новых или модернизированных изделий, в том числе и изделий с пространственно-модифицированными зубчатыми венцами, предшествует конструкторско-технологическая подготовка производства.
К зубчатым колесам и передачам предъявляются повышенные требования по надежности, долговечности, нагрузочной способности при сохранении или уменьшении габаритных размеров. Наиболее перспективным направлением повышения эксплуатационных показателей зубчатых передач является совершенствование геометрии зацепления [1]. В свою очередь работоспособность зубчатых передач зависит от вида и величины перемещений, которые вызваны наличием погрешностей изготовления; погрешностей монтажа зубчатых венцов; погрешностей взаимного положения зубчатых венцов, возникающих в процессе эксплуатации вследствие деформаций элементов зубчатых передач [2, 3]. Наличие в реальном зацеплении погрешностей и деформаций приводит к пространственному характеру контактирования зубьев в зацеплении и к необходимости синтеза новых пространственно-модифицированных зубьев, боковая поверхность которых близка к их естественному износу в процессе эксплуатации.
Конструкторская подготовка производства (КПП) заключается в проектировании новой или модернизации ранее производившейся продукции, а также разработке проекта реконструкции и переоборудования предприятия или его отдельных подразделений. В процессе проектирования определяются назначение и эксплуатационные свойства объекта производства, его конструкция и внешний вид, физико-механические и химические свойства материалов деталей, технико-экономические и другие показатели [4, 5, 6, 7]. Основными целями и задачами КПП являются: непрерывное совершенствование качества продукции, повышение уровня технологичности конструкции, снижение себестоимости изготовления , уменьшения расхода материалов на единицу продукции, снижения эксплуатационных затрат, обеспечение охраны труда и техники безопасности, а также удобство эксплуатации и ремонта изделий.
Продолжением работ по подготовке производства изделия является технологическая подготовка производства (ТПП). Целью ТПП является разработка технологии изготовления изделия в конкретных условиях реального производства, выбор или разработка технологического оборудования и технологического оснащения, режущего и измерительного инструментов. В процессе ТПП решаются следующие основные задачи: отработка изделия на технологичность; разработка технологических маршрутов и процессов; разработка специальной технологической оснастки; технологическое оснащение производства; техническое сопровождение изготовления опытной партии, установочной серии и установившегося серийного производства [8, 9, 10, 11].
Применение информационных технологий при выполнении конструкторскотехнологической подготовки производства (КТПП) является приоритетным направлением модернизации и развития современного предприятия. При этом используются современные технологии: 3D-моделирование, аддитивные технологии для получения прототипов изделий, OMV-технологии, инженерный анализ, автоматизированная подготовка управляющих программ для станков с ЧПУ и автоматизированный контроль параметров точности изделия.
Максимально эффективное использование данных, полученных в результате решения задач синтеза новых пространственно-модифицированных зубьев, возможно во время выполнения КТПП цилиндрических колес с пространственномодифицированными зубчатыми венцами при их представлении в форматах, позволяющих выполнять их автоматическую обработку. Полученные таким образом данные используются при выполнении КТП для создания трехмерных моделей изделий и при подготовке комплектов конструкторской документации. На этапе ТПП данные используются в процессе выполнения технологических расчетов геометрии режущего инструмента, траектории его перемещения в процессе изготовления пространственномодифицированных зубчатых венцов и при выполнении сравнения, во время контроля, соответствия параметров реально нарезанного в процессе формообразования зубчатого венца с теоретически рассчитанными параметрами.
Исходными данными для проведения КТПП изделий с зубчатыми венцами, в том числе и цилиндрических зубчатых колес, являются их основные геометрические характеристики, полученные в результате выполнения проектировочных и проверочных расчетов. Для зубчатых венцов с пространственно-модифицированными зубьями наряду с основными геометрическими характеристиками необходимо иметь описание геометрии боковой поверхности зубьев в виде удобном для построения трехмерных моделей изделий, последующего выполнения комплекта конструкторской документации и проведения расчетов технологических параметров процесса формообразования зубчатых венцов.
Информация о геометрии изделия и его элементов может быть представлена в виде таблицы значений координат [12], матрично-векторным способом [13, 14, 15] и в виде описания геометрии одной кривой [16] или семейством кривых. Задание геометрии изделий координатами отдельных точек выполняется дискретно и применяется в основном для построении двухмерных изображений. В этом случае проведение автоматических расчетов различного вида, с участием координат точек, принадлежащих рассматриваемым пространственным поверхностям имеет ряд существенных ограничений, так как получение результатов может быть только для ограниченного количества таких точек. Матрично-векторный способ задания геометрии изделий позволяет задавать множество точек принадлежащих рассматриваемой поверхности, что в значительной мере способствует автоматизации проводимых расчетов и позволяет получать непрерывную последовательность значения координат точек, принадлежащих поверхности [13, 14, 15]. Однако в случае такого описания поверхности непосредственное ее построение без дополнительной обработки расчетных данных затруднительно.
Описание геометрии боковой поверхности пространственно-модифицированных зубьев семейством кривых, после решения задач профилирования [17, 18], позволяет получать геометрические характеристики изделия непрерывно вдоль одной или нескольких осей детали. Геометрические характеристики изделия получают в привязке к сетке кривых, которые являются линиями пересечения боковой поверхности пространственно-модифицированного зуба с плоскостями параллельными одной из плоскости заданной абсолютной системы координат. Сетка кривых состоит из двух семейств кривых расположенных по длине и по высоте пространственно-модифицированного зуба. В качестве кривых могут быть использованы аналитически описанные гладкие, дважды и более дифференцируемые кривые, с минимальным количеством управляемых элементов. Так в работе [16] в качестве универсального способа описания геометрии профиля зуба цилиндрического зубчатого колеса предлагаются кривые Безье, которые широко используются в системах автоматизированного проектирования. Применение кривых Безье обусловлено рядом их свойств [19, 20].
Цель работы: разработка методики расчета исходных данных для выполнения КТПП цилиндрических колес с пространственно-модифицированными зубчатыми венцами, позволяющей уменьшить сроки выполнения работ путем описания боковой поверхности пространственно-модифицированных зубьев цилиндрических колес семейством сплайнов Безье.
2. Основное содержание и результаты работы
Исходными данными для описания боковой поверхности сеткой сплайнов Безье является густота сетки по длине и по высоте зуба. Количество кривых, на боковой поверхности зуба выбирается в зависимости от точности решаемых задач и сводится к заданию значений координат по длине и по высоте зуба шестерни y1 и z1 [17, 18]. Для выбранных значений координат y1 и z1, в процессе профилирования определяются параметры контактирования (углы поворота шестерни и колеса, угол развернутости эвольвенты и координата по длине зуба колеса z2 и значение третьей координаты x1 [17, 18]. Используя рассчитанные параметры контактирования координаты контактных точек приводятся к одному положению зуба и к его вертикальной оси [18]. После определения координаты x1 получаем распределение координат точек, принадлежащих боковой поверхности зуба с пространственной модификацией, которые в дальнейшем и будут использованы для расчета параметров сплайна Безье. Результаты приведения координат контактных точек на боковой поверхности зуба к одному положению зуба и к его вертикальной оси представлены на рис. 1.
Сплайн Безье определяется зависимостью вида [19, 20]:

где лямдо – параметр сплайна Безье;
N – степень полинома;
Pi – координаты опорных точек;
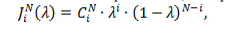
где - биномиальные коэффициенты:
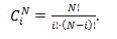
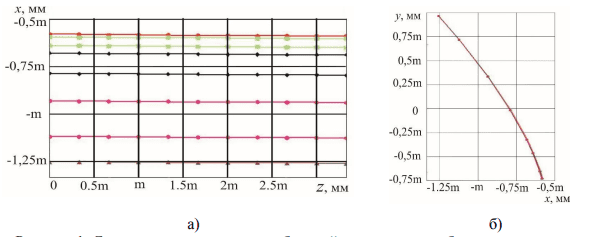
Рисунок 1 – Сетка контактных точек на боковой поверхности зуба шестерни, аппроксимированных семейством сплайнов Безье: а) – по длине зуба; б) – по высоте зуба
Выполним аппроксимацию координат контактных точек на боковой поверхности пространственно-модифицированного зуба цилиндрического зубчатого колеса семейством сплайнов Безье третьего порядка по высоте зуба. Для аппроксимации координат контактных точек (рис. 1. б) используем сплайны Безье третьего порядка. Чтобы найти параметры сплайна Безье третьего порядка необходимо задаваться координатами четырех точек принадлежащих боковой поверхности зуба в рассматриваемом сечении.
Биномиальные коэффициенты для сплайна Безье третьего порядка составят:
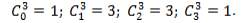
Аппроксимирующие многочлены Бернштейна сплайна Безье третьего порядка:
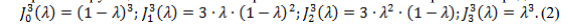
С учетом аппроксимирующих многочленов Бернштейна (2) зависимость (1) примет вид:
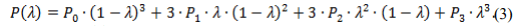
Записав уравнение (3) для каждой из координат рассматриваемой точки на кривой принадлежащей боковой поверхности зуба получим систему уравнений для определения координат точек аппроксимирующего сплайна Безье в Декартовой системе координат:
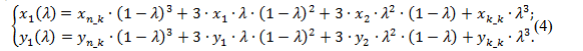
где xn_k, xk_k, yn_k, yk_k – соответственно координаты начальной и конечной точек на кривой описывающей профиль зуба шестерни;
x1, x2, y1, y2 - координаты опорных точек сплайна по толщине и по высоте зуба шестерни.
Неизвестными в системе уравнений (4) являются: параметр сплайна и координаты его опорных точек x1, x2, y1, y2. Известными значениями в системе являются координаты начала и конца кривой, которая описывает профиль зуба, xn_k, xk_k, yn_k, yk_k, а также задаются значения функций x1 и y1. Таким образом, в систему (4) входит 5 неизвестных и для определения координат опорных точек и значения параметра сплайна необходимо записать уравнения системы (4) для координат 4-х точек, лежащих на кривой описывающей профиль зуба в рассматриваемом сечении:
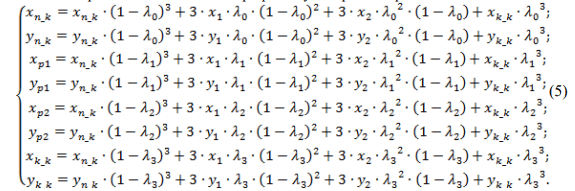
где xp1, xp2, yp1, yp2 - координаты точек принадлежащих кривой, которая описывает профиль зуба шестерни по его высоте в рассматриваемом сечении.
Решив систему относительно параметров сплайна и координат опорных точек , получим систему вида (4), которая позволяет аппроксимировать профиль зуба шестерни в рассматриваемом сечении. Определив параметры сплайнов для ряда сечений, можно выполнить аппроксимацию боковой поверхности пространственно-модифицированного зуба цилиндрического зубчатого колеса семейством сплайнов Безье третьего порядка по высоте зуба.
Выполним аппроксимацию координат контактных точек на боковой поверхности зубьев цилиндрического зубчатого колеса с пространственной геометрией семейством сплайнов Безье четвертого порядка по длине зуба (рис. 1. а). Использование сплайнов Безье 4-го порядка обусловлено необходимостью при выполнении расчета технологических параметров процесса формообразования пространственномодифицированных зубьев оперировать сразу тремя координатами точки на боковой поверхности зуба.
Биномиальные коэффициенты для сплайна Безье четвертого порядка составят:
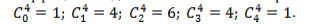
Аппроксимирующие многочлены Бернштейна сплайна Безье третьего порядка:
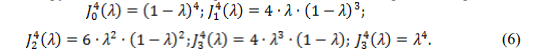
С учетом аппроксимирующих многочленов Бернштейна (2) зависимость (1) примет вид:
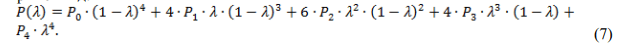
Записав уравнение (7) для каждой из координат рассматриваемой точки на кривой принадлежащей боковой поверхности зуба получим систему уравнений для определения координат точек аппроксимирующего сплайна Безье в Декартовой системе координат:
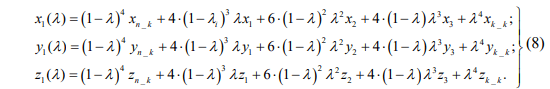
Рисунок 1 – Сетка контактных точек на боковой поверхности зуба шестерни, аппроксимированных семейством сплайнов Безье: а) – по длине зуба; б) – по высоте зуба
где xi, yi, zi - координаты опорных точек сплайна.
Неизвестными в системе уравнений (8) являются: параметр сплайна и координаты опорных точек xi, yi, zi. Известными значениями в системе являются координаты начала и конца кривой, которая описывает профиль зуба, xn_k, xk_k, yn_k, yk_k, zn_k, zk_k, а также задаются значения функций x1, y1 и z1. Таким образом, в систему (8) входит 10 неизвестных и для определения координат опорных точек и значения параметра сплайна необходимо записать уравнения системы (8) для координат 5-ти точек, лежащих на кривой описывающей боковую поверхность зуба по его длине в рассматриваемом сечении:
Решив систему (9) относительно параметров сплайна и координат опорных точек, получим систему вида (8), которая позволяет аппроксимировать линию зуба шестерни в рассматриваемом сечении по его длине.
Определив параметры сплайнов для ряда сечений, можно выполнить аппроксимация геометрии боковой поверхности пространственно-модифицированного зуба цилиндрического зубчатого колеса семейством сплайнов Безье четвертого порядка по длине зуба.
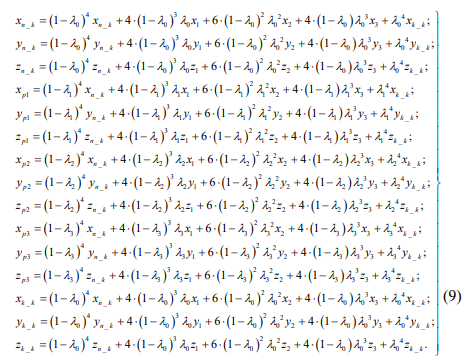
где xpi, ypi, zpi- координаты точек принадлежащих кривой, описывающей боковую поверхность зуба шестерни по его длине.
3. Выводы
В работе представлена методика расчета исходных данных для выполнения конструкторско-технологической подготовки производства цилиндрических колес с пространственно-модифицированными зубчатыми венцами. Методика заключается в аппроксимации координат контактных точек на боковой поверхности зубьев, полученных в результате профилирования, семейством сплайнов Безье третьего порядка. При этом семейство сплайнов Безье в виде сетки расположены в двух направлениях по длине и по высоте зуба. Густота сетки зависит от требуемой точности решаемых в последствии задач и дискретно задается значениями координат по длине и по высоте зуба шестерни.
Полученные зависимости позволяют определять координаты контактных точек на боковой поверхности пространственно-модифицированного зуба в привязке к сетке сплайнов Безье. Данные, полученные таким образом, могут быть использованы при конструировании для построения трехмерных моделей изделий с пространственномодифицированными зубчатыми венцами, определении геометрии режущей части инструмента, определении траектории относительного перемещения инструмента и заготовки, а также при контроле изделий с зубчатыми венцами с пространственной геометрией и позволяют сократить сроки выполнения КТПП.
Список использованной литературы
1. Бабичев, Д. Т. Основы концепции синтеза рабочих поверхностей зубьев цилиндрических передач, обладающих заданной контактной прочностью / Д. Т. Бабичев, М. Г. Сторчак, Д. А. Бабичев // Современное машиностроение. Наука и образование. – 2012. – № 2. – С. 150-160.
2. Артемов, И. И. Система комплексного обеспечения точности зубчатых колес в условиях автоматизированного производства / И. И. Артемов // СТИН. – 1998. – №6. – С. 8–13.
3. Марков, Н. Н. Проявление кинематической погрешности зубчатых колес под действием нагрузок и скоростей вращения / Н. Н. Марков, И. И. Артемов // Вестник машиностроения. – 1986. – №3. – С. 21-23.
4. Гольдштейн, Г. Я. Стратегический инновационный менеджмент: Учебное пособие / Г.Я. Гольдштейн. – Таганрог: Изд-во ТРТУ, 2004. – 267 с.
5. Hill C.W.I., Jones G.R. Strategic Management. – Boston: Houghton Mifflin Co, 1992.
6. Медведева, С. А. Основы технической подготовки производства: уч. пособие /
С. А. Медведева. – СПб: СПбГУ ИТМО, 2010. – 69 с.
7. Ребрин, Ю. И. Основы экономики и управления производством. Конспект лекций. / Ю. И. Ребрин. – Таганрог: Изд-во ТРТУ. – 2000. – 145 с.
8. Вотинова, Е. Б. Основы технологической подготовки производства : учеб. пособие / Е. Б. Вотинова, М. П. Шалимов, А. М. Фивейский.— Екатеринбург : Изд-во Урал. унта, 2017. – 168 с. – ISBN 978-5-7996-2171-1.
9. Schuh, G. Virtuelle Fabrik: neue Marktchansen durch dynamische Netzwerke. Munchen / G. Schuh, K. Millarg, A. Goransson. – Wien: Carl Hanser Verlag. – 1998. – 160 s.
10. John MacKrell Supporting Collaborative Product Definition via Scaleable, WebBased PDM.-Prepared by CIMdata,Inc., 2000. – 16 p.
11. Токликишвили, А. Г. Организация технологической подготовки производства на производственных предприятиях / А. Г. Токликишвили, А. Г. Рогулин, О. В. Колесникова, В. Е. Лелюхин // Современные проблемы науки и образования. – 2015. – № 2-1. – Режим доступа: http://www.science-education.ru/ru/article/view?id=21346 : 30.06.2018.
12. Романов, В. Ф. Расчет зуборезных инструментов. / В. Ф. Романов. – М.: Машиностроение, 1969. — 251 с.
13. Равська, Н. С. Визначення товщини зрізу при зубофрезеруванні черв’ячними фрезами зубчатих коліс / Н. С. Равська, О. А. Охріменко // Надійність інструменту та оптимізація технологічних систем. Збірник наукових праць. – Краматорськ, 2011. – Вип. №28. – С. 3-12.
14. Андросов, С. П. Уравнение режущих кромок червячной модульной фрезы / С. П. Андросов // Приволжский научный вестник. – 2013. – 2(18). – С.4-7.
15. Отт, О.С. Формирование эвольвентных поверхностей деталей дисковым инструментом / О. С. Отт // Вестник МГТУ Станкин, 2010. – №3. – С. 67-71.
16. Воронцов, Б. С. Математическое обеспечение интерактивного синтеза передач зацеплением / Б. С. Воронцов // Вестник НТУ "ХПИ", 2010. – №27 – С. 49- 54. – ISSN 2079-0791.
17. Грубка, Р. М. Обобщенные зависимости для пространственного соединения цилиндрических зубчатых колес, учитывающие наличие погрешностей и деформаций элементов передач / Р. М. Грубка // Прогрессивные технологии и системы машиностроения. – Донецк: ДонНТУ, 2018. – Вып. 3(62). – С. 14-22.
18. Грубка, Р. М. Синтез пространственных геометрий зубьев цилиндрических колес, работающих при наличии погрешностей и деформаций элементов передач / Р. М. Грубка, А. П. Недашковский, А. Н. Михайлов, И. А. Петряева, А. А. Байчоров // Прогрессивные технологии и системы машиностроения. – Донецк: ДонНТУ, 2018. – Вып. 4(63). – С. 17-27.
19. Белов, В. В. Компьютерная реализация решения научно-технических и образовательных задач: учебное пособие / В. В. Белов, И. В. Образцов, В. К. Иванов, Е. Н. Коноплев // Тверь: ТвГТУ, 2015. – 108 с. Режим доступа: https://www.sunspire.ru/articles/ (дата обращения 5.06.2017).